Parametri di un’onda
Per descrivere matematicamente il moto un'onda lungo una corda e il moto di ogni suo elemento abbiamo è necessario usare una funzione del tipo:
$y=f(x,t)$
dove y rappresenta lo spostamento trasversale di ogni elemento della corda in funzione del tempo t e della posizione x dell'elemento lungo la corda. In genere la forma sinusoidale dell'onda come quella che si può propagare lungo una corda può essere espressa indifferentemente sia con una funzione seno sia con una funzione coseno. Noi useremo la funzione seno.
Un’onda sinusoidale in movimento può essere rappresentata attraverso la seguente sequenza di immagini.
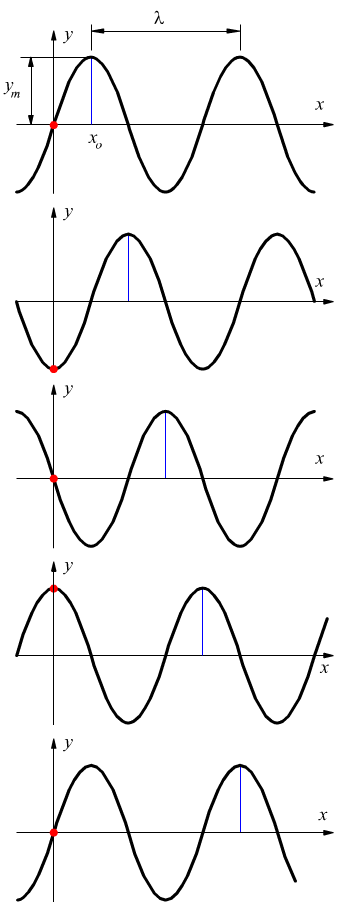
si tratta di una sinusoide che può essere definita dall’equazione
X
L’avanzamento dell'onda è messo in evidenza dalla linea blu che individua
la prima cresta. Al procedere del fenomeno la linea si sposta verso destra
insieme alla forma dell'onda, ma la corda materialmente non fa altro che
muoversi solo lungo l'asse y. Infatti, se attenzioniamo l'elemento di corda
colorato in rosso (in posizione x = 0 nell’immagine iniziale), notiamo che
nella seconda immagine, esso si trova nella posizione più bassa possibile,
perché in quell'istante sta passando attraverso di esso una valle d'onda.
Poi l'elemento torna alla posizione intermedia caratterizzata da y = 0.
Nella quarta immagine si è spostato in su e lo vediamo rappresentato quando
attraverso di esso passa la cresta dell'onda. Da ultimo, si riporta nuovamente
nella posizione intermedia y = 0, dove conclude la sua oscillazione completa.
Ampiezza d'onda
L'ampiezza ym dell'onda, come si vede nell'immagine precedente, è il modulo dello spostamento massimo dalla posizione di equilibrio raggiunto dall'elemento di corda durante la propagazione dell'onda.
La quantità $kx -ωt$ è l' argomento del seno ed è chiamata fase dell'onda. Al transitare dell'onda attraverso un certo elemento situato in posizione x, la fase varia linearmente in funzione del tempo. Di conseguenza il valore del seno varia pure, oscillando tra gli estremi +1 e -1. Quando vale +1 significa che attraverso l'elemento considerato sta transitando una cresta d'onda: in quel momento il valore y dell'elemento è proprio ym. Quando il seno assume il valore -1, significa che attraverso l'elemento considerato sta transitando una valle d'onda: in quel momento il valore y dell'elemento è -ym. In questo modo la funzione seno e la fase dipendente dal tempo rappresentano l'oscillazione dell'elemento di corda, il cui spostamento massimo determina l'ampiezza dell'onda.
Lunghezza d'onda
La lunghezza d'onda λ di un'onda è la distanza (parallelamente alla direzione di propagazione) tra due punti omologhi della forma d'onda, come quelli marcati nella prima immagine della sequenza, che è una rappresentazione dell'onda all'istante t = 0. In questa condizione, l'equazione X diventa:
Numero d'onda angolare
Per definizione i due punti che costituiscono gli estremi di questa lunghezza d'onda, cioè x = xo e x = xo + λ presentano la medesima ordinata y. Per l'ultima equazione scritta si ha dunque:
La funzione seno comincia a ripetersi quando il suo argomento è incrementato di 2π rad, e quindi l'equazione precedente sarà vera se kλ = 2π o se
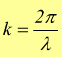$[{rad}/m]$
Nel disegno seguente viene mostrato come la y varia al variare del tempo
in posizione x=0.
(N.B. come nel grafico sull'asse delle ascisse c'è t e non x).
si deduce che in posizione x=0 la corda oscillante si muove su e giù di moto armonico semplice in base all'eq. X se si pone x=0.
Periodo
Definiamo il periodo T di un'onda l'intervallo di tempo dopo il quale il moto di un elemento della corda oscillante, per ogni posizione prefissata x, comincia a ripetersi.
Pulsazione
Trattandosi di un intervallo di tempo, il periodo T di un'onda, viene misurato in secondi.
per la trigonometria questa uguaglianza è verificata solo se $ωt=2π$ cioè se:
pulsazione
$[{rad}/s]$
ω viene chiamata pulsazione o frequenza angolare dell'onda.
Nel Sistema Internazionale la sua unità di misura è il radiante al secondo
[rad/s].
Frequenza
Successivamente può essere introdotta la frequenza dell'onda come:
frequenza
[Hz]
La frequenza viene definita come il numero di oscillazioni effettuate dalla corda vibrante in un secondo.
La frequenza viene misurata in Hertz [Hz].
Costante di fase
Se consideriamo l’eq. X per t=0 in prossimità di x=0 l’onda apparirebbe come la sinusoide disegnata in nero nell’immagine seguente.
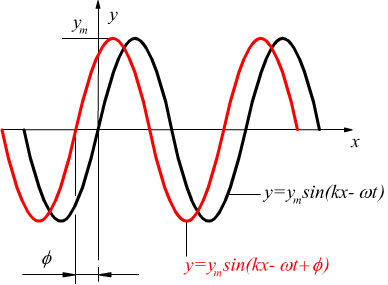
In generale questo non si verifica e l'onda potrebbe essere interessata da uno spostamento orizzontale rispetto a questa posizione. Questa condizione può essere generalizzata introducendo l'angolo di fase ϕ detto anche costante di fase. Nel disegno precedente la costante di fase viene mostrata attraverso la seconda sinusoide evidenziata in rosso. Analiticamente questo tipo di scostamento in ritardo viene descritto modificando l'eq. X come
Nel caso la sinusoide fosse in anticipo, la situazione sarebbe la seguente:
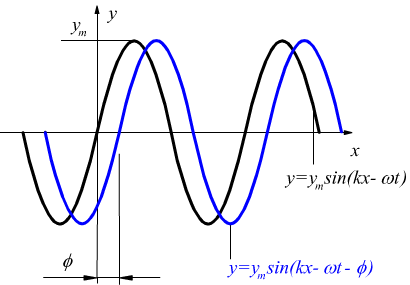
e l'equazione descrittiva la sinusoide in blu sarebbe
