La molla

          

Le molle sono organi meccanici che, sotto l'azione di forze esterne, realizzano significative deformazioni elastiche, per torsione o per flessione, immagazzinando come energia potenziale elastica il lavoro compiuto da queste forze esterne. Una volta esaurita l'azione delle forze esterne le molle ritornano al loro assetto iniziale restituendo il lavoro di deformazione precedentemente immagazzinato.

Qualsiasi corpo può essere, in misura maggiore o minore deformato. Se il corpo in questione può tornare spontaneamente alla sua conformazione iniziale si parla di corpo rigido elastico; se invece la deformazione è irreversibile, si parla di corpo rigido plastico. La differenza tra corpi elastici e plastici è nota; ad es. la gomma da masticare è un corpo plastico, la gomma per cancellare è un corpo elastico.

La forza che permette al corpo di tornare alla sua posizione di equilibrio iniziale (posizione di riposo) è la forza elastica; essa si manifesta sempre opponendosi alla deformazione imposta da una forza esterna tendendo a ripristinare la configurazione iniziale del corpo.

Le molle sono prevalentemente fabbricate in acciaio e sono diffusamente impiegate nelle costruzioni meccaniche. La tipologia di molla più diffusa è la molla a torsione ad elica cilindrica.

Supponiamo di disporre di una molla a riposo in posizione orizzontale e di allungarla tramite una forza esterna F_est.

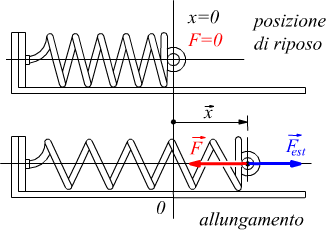
La molla subirà un allungamento che verrà mantenuto fin tanto che sarà presente la forza esterna F→_est. Per il terzo principio della dinamica, per il quale ad ogni azione corrisponde una reazione uguale e contraria, all'interno della molla viene ad instaurarsi una forza elastica F→, che, come si vede dal disegno risulta essere diretta in senso opposto all'allungamento x→ e proporzionale a quest'ultimo. Proporzionale significa che se x raddoppia, F raddoppia; se x triplica, F diventa a sua volta il triplo del suo valore iniziale.
La forza elastica della molla è dunque una forza di richiamo nel senso che se lo spostamento x va in una data direzione rispetto al punto di equilibrio (di riposo della molla) la forza elastica immagazzinata dalla molla è diretta in direzione opposta a tale spostamento.

Un fenomeno analogo avviene nel caso volessimo comprimere la molla applicando una forza F_est esterna ad essa.

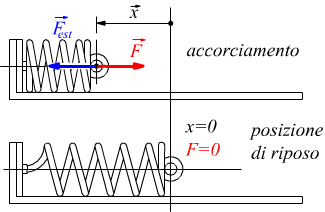
Anche in questo caso la forza elastica della molla F→ risulterà opposta in verso allo spostamento x→ e proporzionale ad esso.
Al cessare dell'azione della forza esterna F_est la forza elastica F tenderà a riportare la molla nella sua posizione di riposo caratterizzata da un allungamento/accorciamento x=0.

La regola di proporzionalità tra la forza elastica e l'allungamento della molla è stato definito per via sperimentale da Hooke nel 1678 e viene formalizzata nella scrittura:

Con questa forma vettoriale si intende che come intensità (modulo) la forza elastica vale F=kx, la direzione di F è la stessa dell'allungamento (o accorciamento) x, il verso della forza elastica F è opposto al verso dell'allungamento (accorciamento). La costante k viene chiamata costante elastica; essendo la forza misurata in Newton [N] e gli allungamenti in metri [m] la costante k ha come unità di misura [N/m] Newton su metro.

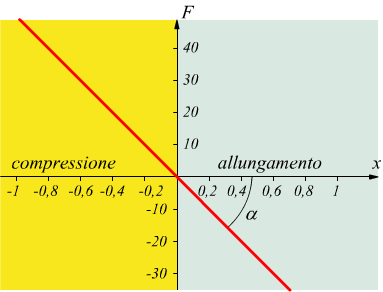
Il legame tra la forza e l'allungamento della molla è, dunque, di tipo lineare, cioè può essere rappresentato sul piano F-x da una linea retta inclinata sul piano F-x. Dal punto di vista geometrico la costante elastica k rappresenta il coefficiente angolare di tale retta, cioè il valore della tangente trigonometrica che la retta forma con l'asse x ( k=tgα ). Da questo fatto si intuisce che più piccolo è il valore di k, più facilmente la molla risulta deformabile. Per contro, maggiore è il valore di k maggior forza occorrerà per deformare la molla.

Avevamo già messo in evidenza delle analogie fra dispositivi meccanici idraulici ed elettrici che qui sotto sono riassunti ancora una volta:

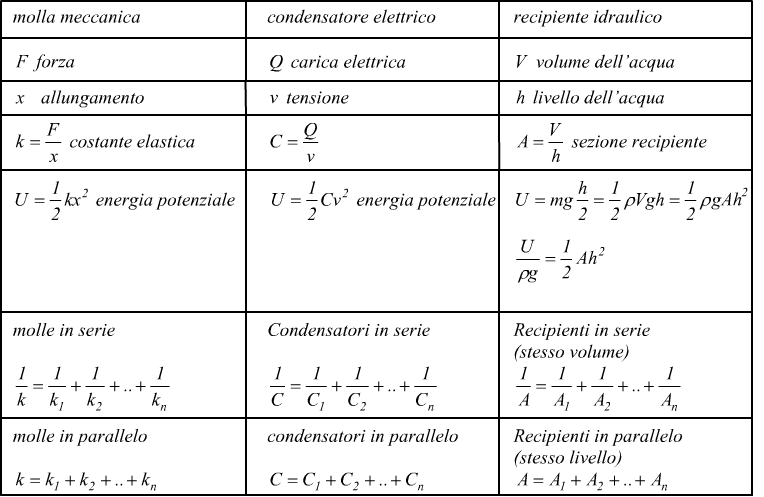
Nota: l'energia potenziale per un recipiente idraulico di massa m deve essere 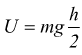perché si pensa di concentrare il peso mg nel baricentro all'altezza h/2.

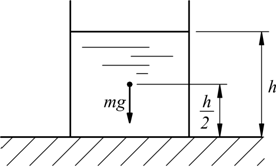
Molle in serie e molle in parallelo

     

E' possibile collegare due molle in serie di costanti elastiche k₁ e k₂ come indicato in figura

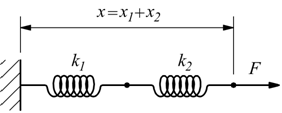
Se consideriamo idealmente le due molle collegate come un'unica molla di costante k L'allungamento toltale sarà:

ma come nel caso delle funi in trazione ciascun tratto delle due molle sarà interessato dalla forza F .

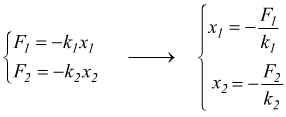           sostituendo

       

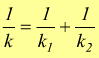
Il comportamento delle molle è simile alla capacità C dei condensatori in elettrotecnica : la costante elastica di una molla formata da due o più molle in serie è minore della minore tra le molle che la costituiscono.

Nel caso delle due molle collegate in parallelo:

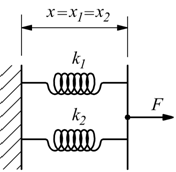
l'allungamento rispettivo sarà identico x₁=x₂=x.   Così sarà possibile scrivere:

considerando idealmente le due molle in parallelo, una unica molla di costante k

     

Energia potenziale elastica

     

Prima dell'invenzione di sistemi elettrici per la fornitura e l'accumulo dell'energia, la molla è stata per lungo tempo l'unico dispositivo in grado di immagazzinare e conservare energia, basti pensare agli orologi analogici (meccanici) dove l'energia per il funzionamento veniva accumulata e rilasciata grazie proprio ad un meccanismo a molla. In questo caso bisognava agire su un rotismo che caricava una molla a spirale comprimendola; la molla poteva poi rilasciare progressivamente l'energia immagazzinata azionando i meccanismi di funzionamento dell'orologio.

Se volessimo effettuare una tale operazione su una semplice molla a torsione comprimendola, dobbiamo tener conto della forza esterna occorrente per la compressione F→_est=kx→, stavolta senza il segno negativo perchè è una forza impressa dall'esterno uguale ed opposta alla forza elastica F della molla.

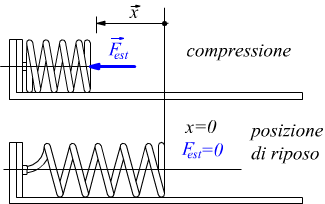
Non basterebbe, in questo caso una semplice moltiplicazione L=F·x per calcolare il lavoro eseguito sulla molla, questo perchè durante il processo di compressione la forza F non rimane costante, occorre, in questo caso ricorrere all'analisi matematica.

questa energia che dall'esterno abbiamo applicato alla molla diventa una energia potenziale elastica, disponibile per l'esecuzione di un futuro eventuale lavoro che la molla potrà eseguire sull'ambiente esterno.

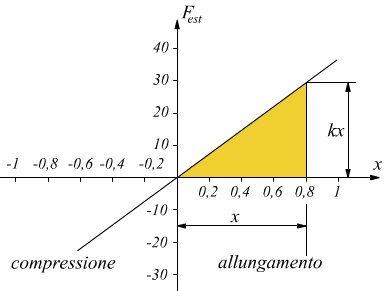
come si vede l'energia immagazzinata dalla molla corrisponde all'area sottesa alla curva di funzione F_est=kx sul piano F_est-x. trattandosi di un triangolo dobbiamo calcolarne l'area (base per altezza diviso 2):

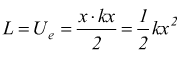     [ J ]

Gli allungamenti precedenti. sono considerati, per brevità e semplicità di calcolo, riferiti alla posizione di riposo x=0.
Questo fatto, in generale può non sussistere, è dunque opportuno correggere la formula precedente come:

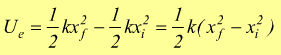      [ J ]

x_i=posizione iniziale
x_f=posizione finale

Quella appena ottenuta è la formula che esprime il lavoro della forza esterna F_est sulla molla.
Essendo tale forza opposta alla forza elastica F della molla, il lavoro effettuato dalla molla sull'ambiente esterno è

Che coincide con la variazione dell'energia potenziale della molla. Il lavoro compiuto dalla forza elastica è dunque

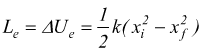
L'importanza della molla come dispositivo fisico sta proprio nel fatto che essa è in grado di accumulare energia potenziale che poi, può trasformarsi in energia cinetica, gradualmente o impulsivamente nel totale rispetto del principio di conservazione dell'energia ΔU=ΔK.

Molle a lamina

     

Sono molle prismatiche ad un solo elemento,come disegnato in figura

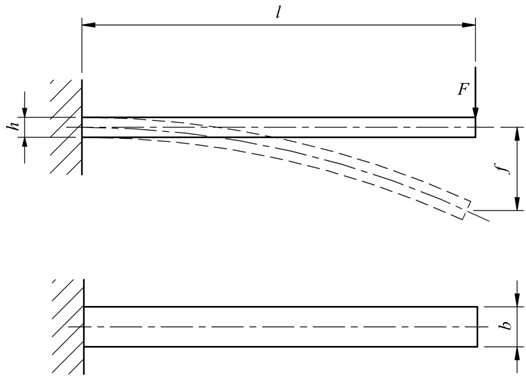
sono incastrate ad un estremo mentre vengono caricate nell'estremo libero. Conoscendo il carico di sicurezza a flessione e le dimensioni della molla ( l=lunghezza,b=larghezza, h=spessore ) si può determinare il carico F applicando l'equazione di stabilità a flessione:

                    con                      

con σ=carico unitario di sicurezza a flessione, mentre il modulo di resistenza di flessione per una sezione rettangolare vale

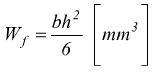                    sostituendo si ha

     

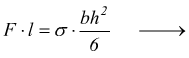
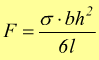
All'estremo libero si genera una deformazione (   freccia   ) di valore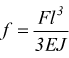   

se la sezione è rettangolare il momento di inerzia è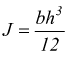   

     

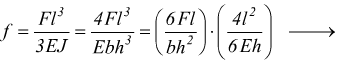
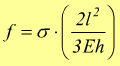
E= modulo di elasticità aflessione per gli acciai E=200.000÷210.000 N/mm².

Il lavoro di deformazione è

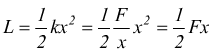     in questo caso l'allungamento x può essere identificato con la freccia f

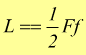              sostituendo

    

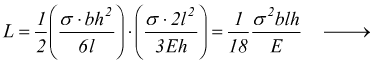
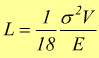
dove V è il volume della molla prismatica.

Molle a balestra

     

Le molle a balestra sono le tipiche molle dei veicoli, costituite da uno strato di foglie metalliche sovrapposte, tenute insieme da una staffa centrale.

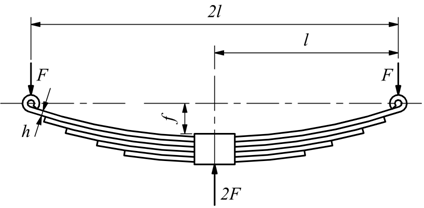
La foglia più lunga costituisce la foglia maestra e alle sue estremità forgiate ad occhio viene applicato il carico. Normalmente per questo tipo di molla si usano le seguenti equazioni:

h=spessore della foglia [mm]
b=larghezza della foglia [mm]
f=freccia massima [mm]
z=numero delle foglie

Molle a torsione

     

In questo tipo di molla la sollecitazione principale è dovuta ad un momento torcente. Il tipo più comune è la molla elicoidale a sezione circolare.

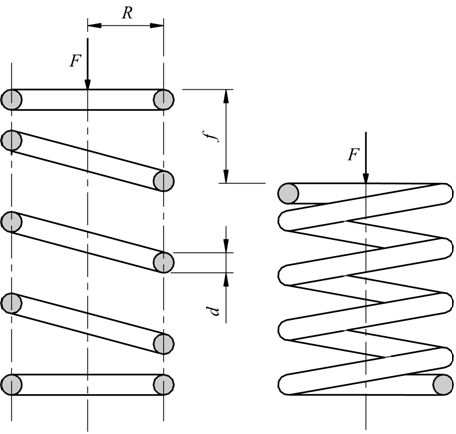
Sotto l'azione del carico F [N] la molla si comprime ed il filo è sollecitato a torsione da un momento torcente

dove con R si indica il raggio medio della molla.Dall'equazione di stabilità a torsione si ha

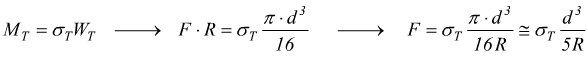
nell'effettivo dimensionamento e verifica di una molla elicoidale interviene un fattore di correzione, si usa infatti τ_max. con

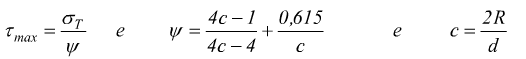
ψ=oefficiente di Wahl
R=raggio dell'elica
d=diametro del filo

questo perché deve essere tenuto conto della curvatura delle spire ed altri parametri.
Il dimensionamento e la verifica avviene dunque con la

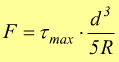
il legame tra la freccia ed il numero delle spire può essere espresso dalla:

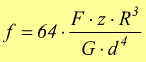
con G=modulo di elasticità a torsione :mediamente 80.000÷90.000 N/mm².