Ruote dentate cilindriche a denti elicoidali

     

La condizione essenziale affinché vi sia continuità di trasmissione in una coppia di ruote dentate, è che due denti in presa non si lascino completamente prima che altri due denti abbiano iniziato l'ingranamento.

Nelle ruote dentate a denti dritti, succede che la coppia di denti in presa, abbandona il contatto su tutta la lunghezza assiale della corona, mentre, simultaneamente , la coppia successiva di denti che sta entrando in presa, inizia il contatto su tutta la lunghezza assiale, questo dà origine a vibrazioni e rumori nocivi.

Per ridurre questi inconvenienti vengono impiegate ruote dentate a denti elicoidali, sopratutto se si tratta di trasmettere potenze elevate.

In questo tipo di ruote, i denti in presa si lasciano gradualmente, e allo stesso modo i denti successivi iniziano l'ingranamento in modo progressivo, in questo modo la trasmissione del moto risulta silenziosa, regolare, senza urti o vibrazioni.

Negli ingranaggi cilindrici elicoidali, i denti non sono paralleli all'asse della ruota, ma si presentano inclinati nell'angolo costante β.
I fianchi, anche se a prima vista possono sembrare rettilinei, assumono l'andamento a elica cilindrica.
La conseguenza più rilevante è che l'ingranamento non avviene più in contemporanea su tutta la lunghezza del dente, bensì su una porzione che trasla lungo la superfice del dente da un'estremità all'altra.

L'arco di ricoprimento può essere posto come cateto verticale del triangolo rettangolo, che ha come secondo cateto la larghezza della fascia dentata ( b ) e come ipotenusa il segmento TX.
La tangente dell'angolo dell'elica è pari al rapporto fra i cateti:

con b=larghezza della fascia dentata. Per la ruota elicoidale, b può essere considerato pari a:

dove m_t è il modulo trasversale e λ=10÷30.

Geometria

     

Considerando il cilindro che ha come asse l'asse ruota e come base il cerchio primitivo. L'intersezione fra il cilindro primitivo e il dente è un elica cilindrica, chiamata elica primitiva.

L'inclinazione della tangente all'elica primitiva, rispetto all'asse della ruota è detta angolo dell'elica β. Indichiamo con p_e il passo dell'elica.
Sviluppando il cilindro in piano, la circonferenza primitiva e la generatrice diventano i due cateti, mentre l'elica diventa l'ipotenusa. I valori tipici di β variano fra 15°÷30° per dentature piccole e fra 5°÷15° per dentature larghe.
Per l'ingranamento di due ruote dentate ad assi paralleli è necessario che le ruote abbiano l'angolo β uguali ma opposti;i passi e moduli devono essere normali ed uguali.
I parametri principali di una ruota dentata cilindrica a denti elicoidali sono:

Passo assiale p_a: è la distanza fra due denti successivi misurata in un piano parallelo all'asse di rotazione

Passo trasversale p_t: è la distanza fra due denti successivi, misurata in un piano perpendicolare all'asse della ruota.

Passo normale p_n : è la distanza fra due denti successivi,misurata in un piano perpendicolare all'asse del dente:

Modulo trasversale m_t: è il modulo riferito al piano frontale della ruota:

modulo normale m_n : è il modulo misurato sul piano normale rispetto al dente; può assumere valori solo determinati valori unificati (vedi tab.).

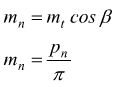
Addendum

Dedendum

Altezza del dente

diametro primitivo d: è il diametro della circonferenza primitiva,misurato su un piano normale dell'asse, dato che solo su tale piano la sezione della ruota è circolare:

numero di denti z: è il rapporto fra il diametro primitivo d e il modulo trasversale m_{t .}

angolo di pressione trasversale θ_t: è l'angolo di pressione misurato sul piano perpendicolare all'asse della ruota.

angolo di pressione normale θ_n: è l'angolo di pressione misurato sul piano normale all'asse della ruota; ha il valore unificato di 20°:

eventuali altri parametri sono ottenibili in base a quanto detto per le ruote cilindriche a denti diritti.

Numero minimo di denti

     

Per calcolare il numero minimo di denti da assegnare ad una ruota elicoidale si fa riferimento ad una ruota fittizia a denti dritti su cui calcolare in numero minimo di denti.
Questa ruota fittizia viene ottenuta nel seguente modo:

Si individua un piano normale al dente passante per il suo punto medio ottenendo la sezione A-A indicata in figura.

Si determina, in questo modo, una figura ellittica con semiasse minore pari al raggio primitivo R mentre il semiasse maggiore ha valore R/cosβ.

Si costruisce un tratto di circonferenza tangente internamente all'ellisse nel suo punto a semiasse minore con raggio R/cosβ .

In questo modo si determina la circonferenza osculatrice di raggio R/cos²β (linea tratteggiata) che individua il cerchio primitivo ospitante il numero ideale dei denti (dritti); indicando:
z=numero dei denti ruota elicoidale
z_id=numero dei denti della ruota ideale                                         si ha in definitiva:

Spinte periferiche

     

Dato che i denti elicoidali sono inclinati dell'angolo β rispetto all'asse di rotazione della ruota; lo sforzo periferico F che questa deve trasmettere, si decompone in varie componenti :
F_n=spinta normale; che è la pressione fra i denti durante l'ingranamento ed
F_a=spinta assiale parallela all'asse della ruota che si scarica sui cuscinetti su cui l'albero viene calettato;
poi c'è
F_t=forza tangenziale trasmessa che può essere ottenuta

tramite la coppia trasmessa        o tramite la potenza trasmessa .

Si vede come sia   

Sezionando la ruota col piano K-K si evidenzia la forza radiale F_r ortogonale alla forza trasmessa F_t ; queste due forze vanno a comporre una risultante F_c inclinata, oltre che dell'angolo β rispetto all'asse di rotazione, dell'angolo di pressione trasversale θ_t rispetto alla forza totale F. Si ricava:

Dimensionamento di ruote dentate cilindriche a denti elicoidali

     

In questo caso la formula per il dimensionamento a flessione delle ruote dentate a denti diritti deve essere corretta, determinando il modulo normale come:

dove σ_T ( o σ_adm ) è il carico di sicurezza unitario dinamico, già tabulato in precedenza.
Poi osservando che normalmente λ=10

oppure si può determinare il modulo trasversale con la seguente formula pratica:

Dove F è la forza periferica; quest'ultima formula viene ottenuta eseguendo la semplificazione già vista nel caso degli ingranaggi a denti diritti.