Ingranaggi
Attraverso meccanismi come le ruote in frizione possono essere trasmesse potenze molto limitate, max 8 kW per l'impossibilità di elevare molto la pressione normale della ruota ( pn ). Per poter trasmettere potenze di ordine superiore bisogna usare le ruote dentate.
In questo tipo di ruote, la forza periferica trasmissibile, non dipende più dal coefficiente di attrito e dalla pressione normale, ma dalla resistenza dei denti ingrananti fra loro.

I denti devono essere opportunamente dimensionati in modo da poter trasmettere potenze anche elevatissime a qualsiasi velocità di rotazione. I materiali generalmente impiegati sono:
Acciai al carbonio bonificato per ingranaggi di resistenza modesta di costruzione semplice ed economica.
Acciai speciali cementati, al nichel, al nichel-cromo, al nichel-molibdeno, superficialmente durissimi, resistenti all'usura ma internamente tenaci e di conseguenza resistenti alle sollecitazioni dinamiche.
Ghisa, per ingranaggi moderatamente sollecitati senza urti Bronzo, usato solo in casi particolari come i riduttori di velocità a ruota elicoidale-vite perpetua.
Leghe leggere come l'alluminio e il magnesio, usate su ruote poco sollecitate che devono resistere alla corrosione.
Resine sintetiche come la bachelite, usata in ruote dentate a bassa velocità per la trasmissione di potenze a funzionamento silenzioso.
Le modalità di trasmissione del moto possono essere:
fra alberi paralleli, con ruote dentate a denti diritti o elicoidali.
fra alberi concorrenti, con ruote dentate coniche a denti diritti o elicoidali.
fra alberi sghembi con ruote dentate a denti elicoidali.
Ruote dentate cilindriche a denti diritti
Sono dotate di denti disposti parallelamente all'asse della ruota e sono usate per trasmettere potenze fra alberi paralleli. Il meccanismo è costituito da due ruote dentate ingrananti fra loro ed è denominato ingranaggio.
La ruota motrice trasmette il moto facendo pressione sui denti della ruota condotta che gira in senso contrario alla prima.
Si chiama rocchetto o pignone la ruota col minor numero dei denti quella col maggior numero di denti si chiama ruota.
Una ruota dentata è formata dalla corona dentata e dal mozzo unite da un disco pieno o forato o da razze nel caso di ruote di grosso diametro. I denti devono essere opportunamente sagomati e profilati in modo da avere il massimo rendimento di trasmissione, quello più usato è quello il profilo ad evolvente.
Si chiama diametro primitivo di una ruota dentata il diametro associato alla circonferenza che passa dove la larghezza dei denti è uguale alla larghezza dei vani.

Le circonferenze primitive di una coppia di ruote dentate, sono quindi
tangenti fra loro e formano una linea di contatto durante l'ingranamento.
D'ora in poi indichiamo:
d1=diametro primitivo della ruota motrice
d2=diametro primitivo della ruota condotta
z1=numero di denti della ruota motrice
z2=numero di denti della ruota condotta
n1=numero di giri al minuto della ruota motrice
n2=numero di giri al minuto della ruota condotta
L'interasse fra le due ruote risulta essere: 
Il rapporto di trasmissione: 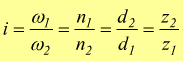
Si riconoscono, inoltre, i seguenti elementi:
Il cerchio di testa che limita esternamente la sommità dei denti e determina il diametro di testa (diametro esterno de ) .
Il cerchio primitivo :è la circonferenza lungo la quale avviene il contatto della coppia di ruote dentate ed è associato al diametro primitivo d.
Il cerchio di piede :limita inferiormente la base dei denti e determina il diametro del piede (diametro interno di ).
Il passo della dentatura (p): è la lunghezza dell'arco di circonferenza compreso fra due profili dentati omologhi consecutivi.
L'altezza del dente (h) è la distanza radiale fra il cerchio di testa e quello di piede.
La costa del dente ( C ) è la parte compresa tra il cerchio primitivo e quello di testa, misurata sull'asse del dente ed è anche denominata addendum.
Il fianco del dente (F) è la parte di dente compresa fra il cerchio del piede e il cerchio primitivo denominata anche dedendum.
Le ruote dentate sono dimensionate tramite il sistema modulare in cui si valuta il modulo (m)
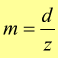
Il passo della dentatura può essere ottenuto dalla formula
![]()
Due ruote ingrananti fra loro devono avere lo stesso passo, quindi hanno lo stesso modulo. inoltre si ha:
![]() costa
(addendum)
costa
(addendum)
![]() fianco (dedendum)
fianco (dedendum)
![]() altezza
del dente
altezza
del dente
![]() diametro
esterno (diametro di testa)
diametro
esterno (diametro di testa)
![]() diametro
interno (diametro di piede)
diametro
interno (diametro di piede)
![]() larghezza
del dente
larghezza
del dente
nella pratica il coefficiente λ≅10

Il diametro di testa è uguale al diametro primitivo più due addendum, cioè due moduli:
![]() essendo
essendo ![]() avremo:
avremo:

Questa formula è molto utile, perchè quando si rompe una ruota ( si rompe un dente ) non si trova quasi mai la documentazione di quel pezzo; ma con questa formula, misurando il diametro esterno e contando i denti, si riesce ad ottenere il modulo. Poi si applica il seguente algoritmo:
: modulo (mm)
così si può ricostruire la ruota.
Profilo ad evolvente
Se il moto fra due ruote dentate deve essere trasmesso con regolarità,
è necessario che i denti vengano a contatto fra loro senza che vi siano
strisciamenti e che il rapporto di trasmissione sia costante.
Questo si verifica solo se il punto di contatto delle circonferenze primitive
si trova sempre sulla congiungente delle due ruote. Queste condizioni
di moto, sono verificate solo da due tipi di profili: quello cicloidale
e quello ad evolvente. In pratica viene sempre adottato quest'ultimo perché
è facile da lavorare ed è di forma semplice.

Nella dentatura ad evolvente la direzione della spinta Q che i denti della motrice trasmettono alla condotta forma sempre un angolo θ con la tangente fra le due circonferenze primitive. Scomponendo Q Si ha la componente tangenziale F e la componente normale N. Dalla

si ottiene il momento torcente ed
 con
rp raggio primitivo della ruota.
con
rp raggio primitivo della ruota.
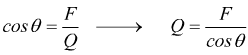
si ottiene così la spinta sulla retta di pressione.
L'angolo di pressione θ è sempre un parametro importante;
può valere 15° oppure 20° ma ormai in Italia si ha un valore
normalizzato di 20°.
In base all'angolo di pressione e al rapporto di trasmissione è
possibile ottenere il numero minimo dei denti del rocchetto ( la ruota
più piccola ) di una coppia di ruote dentate, tramite la formula pratica:

anche questa formula è importante perchè associata al minimo ingombro dell'ingranaggio.
Dimensionamento di ruote dentate
Per il dimensionamento delle ruote dentate, il sistema di calcolo più comune è il metodo di Reuleaux; esso è basato sull'ipotesi che il dente sia sollecitato a flessione. Per una generica sezione, si ha Mf il momento flettente e Wf il modulo di resistenza; mentre con σT ( σamd ) la massima tensione normale ammissibile che tiene conto della condizione di sollecitazione dinamica cui è sottoposta la ruota , l'equazione di stabilità sarebbe .
![]() con
con 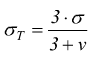 e
con
e
con 
R=carico unitario di rottura
σ=carico unitario di sicurezza
ns=grado di sicurezza 3÷5 per gli acciai (
scegliamo ns=5 perchè il carico è dinamico
)
v=velocità periferica della ruota sul raggio primitivo
Bisogna dire che il valore 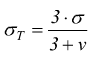 dipende
non solo dalla velocità periferica della ruota, ma anche dalla precisione
della lavorazione, del montaggio e dalla intensità del carico.
dipende
non solo dalla velocità periferica della ruota, ma anche dalla precisione
della lavorazione, del montaggio e dalla intensità del carico.
Per ingranaggi molto lenti può anche essere sufficiente σT=σ
ma per ingranaggi molto veloci e di buona precisione può essere indicato
un coefficiente di riduzione fino a


Ora, supponendo che il dente abbia spessore costante si sa che la sezione maggiormente sollecitata è quella di incastro alla base del dente stesso, dove appunto il momento flettente massimo vale F·h.Se chiamiamo b la larghezza di base del dente si ha che il modulo di resistenza a flessione vale
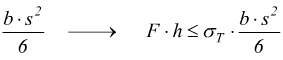
Poi sappiamo che

![]() (
addendum+dedendum ) mentre è
(
addendum+dedendum ) mentre è
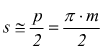
abbiamo già detto che la larghezza b del dente è direttamente proporzionale al modulo
![]() poi si ha:
poi si ha:
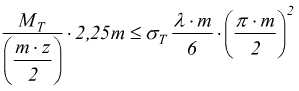
esplicitando rispetto al modulo m
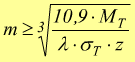
per 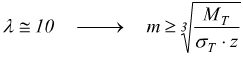
In talune circostanze, può essere comodo esprimere la precedente relazione in funzione dello sforzo periferico F.
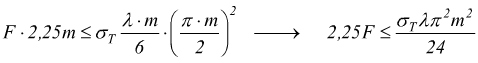
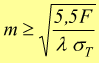
per 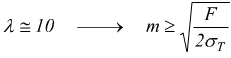
Valori di σT ottenuti empiricamente in N/mm2 sono:
| Velocità periferica v (m/s) | < 0,5 | 2 | 4 | 6 | 8 | 10 | 12 |
| Ghisa | 40 | 24 | 17 | 13 | 11 | 9 | 8 |
| Bronzo | 60 | 36 | 26 | 20 | 16 | 14 | 12 |
| Acciaio di qualità | 100 | 60 | 43 | 33 | 27 | 23 | 20 |
| Acciaio al nichel | 180 | 110 | 77 | 60 | 49 | 41 | 36 |
| Acciaio al nichel-cromo | 500 | 300 | 210 | 166 | 136 | 115 | 110 |
I valori dei moduli normali sono unificati, il valore del modulo trovato deve poi essere assimilato ai valori riportati di seguito.
|
Tabella dei moduli normali
|
|||||||||||||
|
0,5
|
0,75
|
1
|
1,125
|
1,25
|
1,375
|
1,5
|
1,75
|
2
|
2,25
|
2,5
|
2,75
|
3
|
3,25
|
|
3,5
|
3,75
|
4
|
4,5
|
5
|
5,5
|
6
|
6,5
|
7
|
8
|
9
|
10
|
11
|
12
|
|
14
|
16
|
18
|
20
|
22
|
25
|
28
|
32
|
36
|
40
|
45
|
50
|
||
in giallo i valori da preferire e di conseguenza di uso più frequente.
Un accoppiamento fra due ruote dentate, può essere ideato in prima
istanza se abbiamo un numero minimo di dati iniziali quali :
P=potenza trasmessa
n1=velocità della ruota motrice
i=rapporto di trasmissione
R=carico di rottura del materiale di costruzione
λ='snellezza' :parametro legato allo spessore della ruota
Può essere applicata la seguente procedura::
1) Si calcola il numero di denti della ruota motrice z1
con la 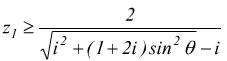
usando un valore di θ=20° . Si calcola z2 numero di
denti della ruota mossa. 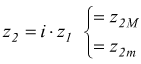
in generale risulta un numero con la virgola; fra i due valori possibili
z2M=approssimazione per eccesso all'intero più grande
z2m=approssimazione per difetto all'intero più piccolo
si sceglie quello che fornisce il rapporto di trasmissione più vicino a quello assegnato nei dati. Se non ci sono problemi di ingombro si può scegliere z1 arbitrariamente ma certamente con z1>15.
2) Si calcola la coppia
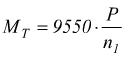
Ricordiamoci che se mettiamo la potenza in watt, il momento torcente sarà Nmm..
3) Essendo le condizioni di lavoro di tipo dinamico si sceglie un grado
di sicurezza alto:n=5 
4) Si ipotizza una velocità periferica nominale vn=2 e si
applica la formula 
5) Si trova il modulo 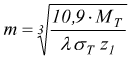 che
sarà approssimato all'intero più grande.
che
sarà approssimato all'intero più grande.
6) Si calcolano i diametri primitivi delle due ruote d1=m·z1 e d2=m·z2
7) Si valuta la velocità periferica effettiva: 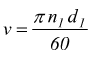
Se v<vn si torna al punto 4 e si ripetono i calcoli con
un valore di vn incrementato di 1.
Se v>vn il modulo individuato è accettabile.
Il problema è che a priori, non si conosce la velocità periferica dell'ingranaggio, al massimo si può averne una vaga idea, per cui bisogna procedere per tentativi.
n1 [g/m]
i
R [N/mm2]
λ
Negli esercizi 16 - 17 - 18 viene usato questo metodo.
Rendimento di ruote dentate
Durante la trasmissione del moto con ruote dentate si ha sempre uno strisciamento fra i denti in presa con conseguente perdita di energia per attrito. Ovviamente il rendimento di un ingranaggio dipende dal suo grado di finitura e dalla lubrificazione. Si può trovare il rendimento di una coppia di ruote dentate con la formula pratica:
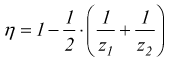
L'usura è elevata e il rendimento è basso nelle trasmissioni a ruota-vite senza fine e con le ruote a denti elicoidali. ad assi sghembi. Questi tipi di trasmissione devono essere evitati quando la potenza da trasmettere è elevata.
 edutecnica
edutecnica