Momento di una forza

     

Il momento di una forza rispetto ad un punto P (scelto arbitrariamente) è il prodotto dell'intensità della forza per la distanza del punto P dalla retta di azione della forza stessa.

           

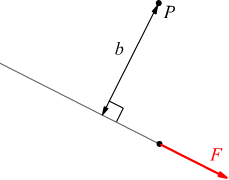
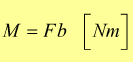
Il punto P prende il nome di polo mentre la sua distanza dalla retta di azione della forza F→, cioè la normale condotta dal polo P su tale retta viene chiamata braccio.

Essendo la forza una grandezza vettoriale, anche il momento è un vettore.

Dal punto di vista geometrico il vettore M→ è perpendicolare al piano definito dal polo P e dalla retta di azione della forza F→.
L'effetto del momento di una forza è sempre quello di produrre una rotazione attorno al punto di riferimento P chiamato, appunto, polo dei momenti.

 

La formula precedente deriva da una definizione più rigorosa del momento di una forza:

       

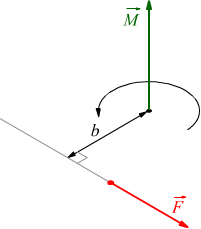
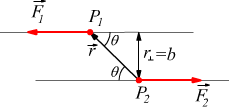
Il momento di una forza è dato dal prodotto vettoriale tra la forza F→ e il vettore spostamento r→ tra il polo P ed il punto di applicazione del vettore F→.

si vede come b=r_⊥ vettore componente di r→ perpendicolare ad F→.

Per le coppie di forze, si assume convenzionalmente come positivo il senso di rotazione antiorario. In tal caso il vettore momento sarà orientato perpendicolarmente al piano di giacitura della coppia di forze e il verso sarà uscente dalla pagina e diretto verso l'osservatore.

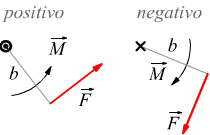
Al contrario se il senso di rotazione è orario, il vettore momento M→ sarà entrante nella pagina.

Una semplice regola pratica che permette di stabilire direzione e verso di un momento di forze è la regola della mano destra: se si dispongono le dita secondo il senso di rotazione della coppia, il pollice indica la direzione e il verso del momento.

Notazione vettoriale

     

Come si vede dai disegni, sia la forza che la distanza di quest'ultima da un polo sono dei vettori nello spazio bidimensionale, il momento di una forza è un terzo vettore che si trova collocato lungo un asse perpendicolare al piano definito dai vettori F→ ed  r→ e passante per il punto di applicazione di r→ .
Può essere allora opportuno rappresentare i tre vettori con la notazione vettoriale dei versori î, ĵ e k̂.
In tal caso la forza F→ che genera il momento verrebbe qualificata come.

Dove F_x, F_y, ed F_z sono le componenti lungo gli assi x, y e z della forza F mentre î, ĵ e k̂ sono dei vettori unitari di lunghezza unitaria, anche chiamati versori il cui unico scopo è quello di indicare la direzione e il verso degli assi x, y e z.
Il momento della forza F rispetto al polo scelto potrà essere allora calcolato con la tecnica matriciale:

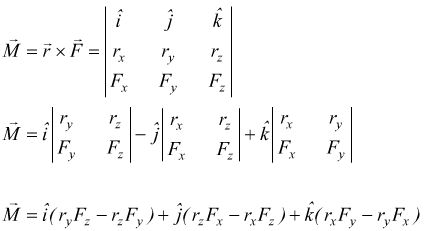
Teorema di Varignon

     

Ipotizzando di avere un sistema di forza complanari F₁ F₂..F_n ; il teorema di Varignon afferma che

In un sistema di forze complanari la somma algebrica dei momenti delle singole forze, rispetto ad un generico punto P del piano, è uguale al momento della risultante del sistema di forze, valutato rispetto allo stesso punto.

Se pensiamo ad un sistema con tre forze F₁ F₂ ed F₃ valutando i momenti rispetto ad un polo scelto arbitrariamente:

 

 

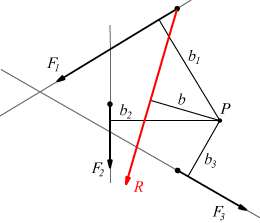
o anche

Il teorema di Varignon anche chiamato teorema dei momenti è molto utile per stabilire rapidamente la posizione della risultante di un sistema di forze parallele.

Se ci riferiamo al sistema di forze qui sotto disegnato, scelto arbitrariamente un polo P sulla congiungente i punti di applicazione delle forze F₁ F₂ ed F₃ :

            

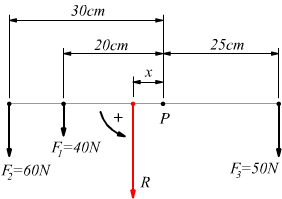
il teorema dei momenti appena enunciato afferma

perchè il momento M₃ tende a ruotare in senso orario dunque negativo per convenzione

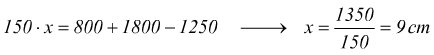
Leve

     

Tra i dispositivi il cui funzionamento si basa sul principio del momento di forze, troviamo le leve. Le leve sono degli apparati meccanici utilizzati per amplificare le forze.
La leva è costituita da un'asta rigida che può ruotare attorno ad un punto fisso chiamato fulcro. chiamiamo :

• R la forza resistente;
• b il braccio della forza resistente;
• F la forza motrice;
• d il braccio della forza motrice.

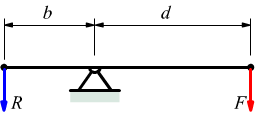
in condizioni di equilibrio il momento della forza motrice F deve uguagliare il momento della forza resistente R:

Più in generale si dice che un sistema di forze è in equilibrio quando è nulla la somma algebrica dei momenti (sempre rispetto allo stesso punto) delle varie forza che lo costituiscono; cioè quando è nullo il momento risultante.

Affinchè la forza motrice possa vincere contro una forza resistente maggiore di esse occorre che il braccio d della forza F sia maggiore del braccio b della forza resistente R. Se si verifica quesa condizione la leva è chiamata vantaggiosa.
Le leve possono essere classificate in tre categorie:

Leve di primo genere : il fulcro è posto tra le due forze F ed R.

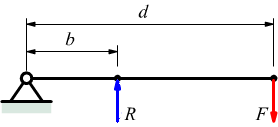
Leve di secondo genere : la forza resistente R si trova tra il fulcro e la forza motrice F.

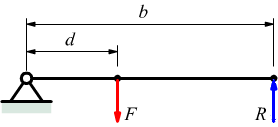
Leve di terzo genere : la forza motrice F si trova tra il fulcro e la forza resistente R.

Le leve di primo genere possono essere sia vantaggiose che svantaggiose a secondo della lunghezza dei bracci b e d.
Le leve di secondo genere sono sempre vantaggiose perchè d>b.
Le leve di terzo genere sono sempre svantaggiose perchè d<b.

Coppia di forze

     

Una coppia di forze è un sistema composto da due forze (F₁=F₂=F) complanari, uguali in modulo (intensità) e parallele (aventi la stessa direzione) opposte in verso, applicate a due punti diversi di un corpo rigido.

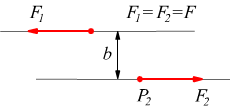
Il braccio della coppia è la distanza fra le due rette di azione delle due forze. Il momento della coppia è il prodotto del braccio per l'intensità di una delle due forze.

                         

Il momento di una coppia non dipende dal polo rispetto al quale viene calcolato; infatti se per comodità lo calcoliamo rispetto al polo P₂: (la scelta del polo è sempre arbitraria)

Nello schema sottostante, si valuta il momento M di una forza F (in verde) rispetto al polo di coordinate (0,0).
Si può modificare la posizione di F spostando la sua coda o la sua punta sul piano.
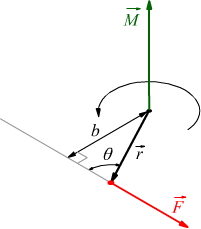
Il braccio b è disegnato in viola. |b| è la lunghezza (modulo) di b mentre ∠b è l'angolo che il braccio b forma con l'asse orizzontale (x).
Nella rappresentazione si assume una proporzionalità 1m ∝ 1px.
Allo stesso modo |F| è il modulo della forza F mentre ∠F è l'angolo che F forma con l'orizzontale x.
Nei dati, θ è l'angolo reciproco tra F e b :

ed è proprio questo angolo che deve essere usato nella formula per il calcolo del momento. Si nota come in questo caso manteniamo r≡b mentre per calcolare il momento usiamo la forma equivalente

: x [m] : |F| [N] : |b| [m] : θ [deg]

: y [m] : ∠F [deg] : ∠b [deg]