Moto circolare uniforme

La traiettoria di un punto è la linea formata dall'insieme delle posizioni che il punto stesso occupa in tempi diversi. Un punto P descrive una traiettoria circolare quando si muove rimanendo sempre alla stessa distanza da punto fisso O.
Se il movimento avviene con velocità costante nel tempo il moto viene definito circolare uniforme.

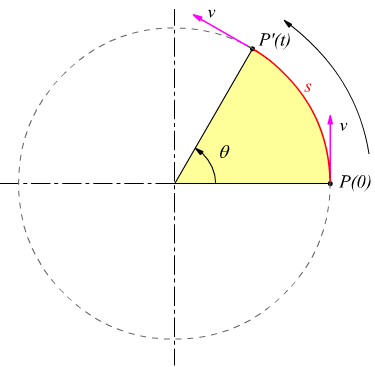
Ipotizziamo che il punto P ell'istante iniziale t_o=0 si trovi nella posizione disegnata. Dopo un certo intervallo di tempo t il punto mobile si è spostato in P' descrivendo l'arco di circonferenza PP' equivalente allo spazio percorso nel tempo considerato .
E' possibile definire la velocità media di P con il rapporto

[ m/s ] velocità periferica

tra lo spazio percorso s( lunghezza dell'arco di circonferenza PP') e il relativo tempo impiegato.

La formula scritta definisce velocità periferica del punto mobile.

Se il moto è uniforme il vettore velocità periferica è di intensità (modulo) costante ed è una grandezza vettoriale che può essere rappresentata da un vettore tangente alla circonferenza nel punto P ad un istante assegnato.

La velocità periferica non è l'unica velocità che si prende in considerazione nel moto circolare .

Osservando il movimento del raggio OP effettua passando in posizione OP' descrivendo un angolo θ possiamo definire la velocità angolare ω come il rapporto tra l'angolo al centro descritto dal raggio OP ed il tempo impiegato per descriverlo.

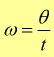[rad/s]

Sapendo che tra la lunghezza di un arco di circonferenza, il raggio e l'angolo al centro esiste la relazione

possiamo esprimere la velocità periferica del punto P come

In un moto circolare uniforme la durata di un giro completo di circonferenza è chiamata periodo e si indica col simbolo T [secondi].
Il numero di giri compiuti in un secondo è chiamato frequenza f [Hz (hertz)] e si indica con il simbolo f. Vi è quindi la relazione

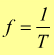
Se il moto circolare è uniforme, la velocità periferica può essere calcolata come il rapporto tra la circonferenza ed il tempo impiegato a percorrerla:

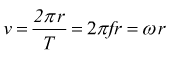quindi si ha

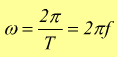
Se il punto P percorre una circonferenza di raggio r, compiendo n giri al minuto (giri/min) in un giro percorrerà uno spazio pari alla circonferenza

e in un minuto (60 sec.) percorrerà uno spazio pari a quindi la sua velocità periferica è

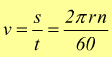
ricordando che è

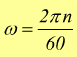
r : 1 m

θ : 45°

t : 1 s

Moto circolare uniformemente accelerato

Se il punto P percorre la circonferenza e la sua velocità periferica v non si mantiene costante, ma varia nell'intervallo di tempo t dal valore iniziale v_o al valore finale v può essere definita l'accelerazione periferica (o tangenziale)

[ m/s² ]

Se il moto avviene con progressione costante nel tempo il moto viene definito circolare uniformemente accelerato.

Dato che abbiamo specificato anche una seconda velocità (ω=velocità angolare), definiamo l'accelerazione angolare:

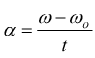se ω_o=0 e v_o=ω_o·r=0 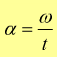[ rad/s² ]

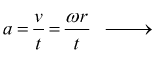
L'arco di circonferenza s percorso nel tempo t dal punto P con moto uniformemente accelerato può essere ricavato con la stessa formula del moto rettilineo

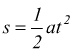se vi è la presenza di una velocità iniziale v_o: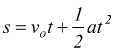

sappiamo che la relazione tra l'arco di circonferenza s e l'angolo al centro è

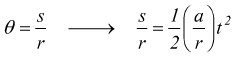dunque risulta

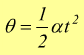[ rad ] questo se il punto mobile P parte da fermo.

Se invece già all'istante t_o=0 P è dotato di una velocità v_o ricordando che ω_o=v_o/r si ha

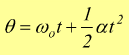
Nel seguente schema, un punto mobile, esegue per un tempo iniziale t(i) un moto circolare uniforme ad una velocità di n(i) giri/min, poi subisce una accelerazione (o decelerazione) per un tempo t(a) fino a portarsi alla velocità n(f) alla quale rimane in modo permanente.

Ovviamente se all'istante t=0 il mobile ha già percorso un angolo θ_o dobbiamo tenerne conto modificando la formula precedente

Combinando due delle formule precedentemente trovate per il moto circolare uniformemente accelerato è possibile ottenere una importante relazione che lega tra loro velocità, posizione e accelerazione angolare, indipendentemente dal tempo

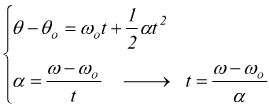
sostituendo questa espressione del tempo nella prima equazione del sistema si avrà

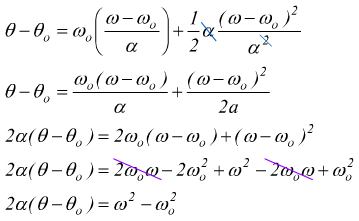
si ottiene dunque

Ricordiamoci poi che se tra le due formule del moto rotatorio

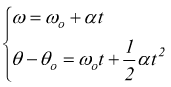
eliminiamo l'accelerazione angolare

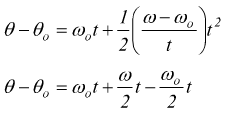
otteniamo un'ulteriore utile relazione.

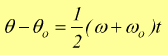
Accelerazione centripeta

Nel caso del moto circolare uniforme, il vettore v, tangente alla circonferenza non varia nel tempo come intensità ma varia continuamente in direzione.
Chiamiamo v' la velocità periferica nel punto P' e v la velocità periferica nel punto P.
Ovviamente in modulo (intensità) sarà sempre v'=v. Consideriamo la differenza Δv=v'-v in rapporto al tempo t che il punto P impiega a spostarsi in P'.

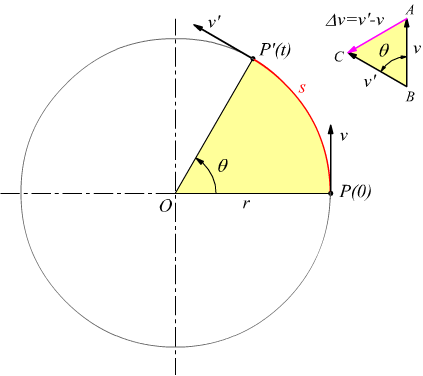
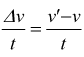
Valutiamo tramite un disegno la differenza vettoriale tra v e v' ottenendo il Δv.
Se l'arco s=PP' è sufficientemente piccolo il settore circolare POP' può essere approssimato ad un triangolo simile ad ABC. In questo caso scriveremo

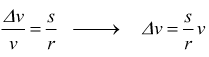quindi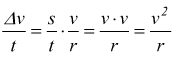

abbiamo in questo modo ricavato l'accelerazione centripeta. Nel moto circolare uniforme l'accelerazione tangenziale è nulla, l'accelerazione centripeta ha valore:

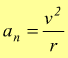[ m/s² ]

sapendo che v=ω·r il suo valore è anche

L'accelerazione centripeta (o accelerazione normale perchè sempre perpendicolare alla traiettoria) è una grandezza vettoriale. Il suo vettore rappresentativo ha punto di applicazione nel punto mobile P ed è sempre orientato verso il cento O della circonferenza descritta. Durante il moto circolare uniforme l'accelerazione centripeta mantiene costante il suo valore essendo costanti la velocità periferica v ed il raggio r.

Una trattazione di questi argomenti che però richiede qualche nozione di analisi matematica è riportata nella pagina del moto curvilineo.