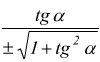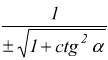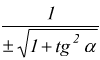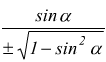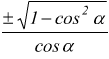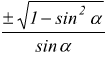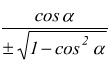Formulario di trigonometria
Sistema di riferimento per gli angoli
Disegniamo una circonferenza con centro O nell'origine di due assi cartesiani
ortogonali orientati x ed y.
Sulla circonferenza consideriamo il punto A, intersezione col semiasse x
positivo; assumiamo il punto A come origine degli archi.
Consideriamo poi un angolo qualsiasi θ che abbia il suo vertice coincidente
con l'origine O degli assi e il suo primo lato sul'asse delle ascisse, che
viene detto origine degli angoli.
E' convenzione considerare gli angoli sempre secondo questa disposizione,
fissando come positivo, il verso di rotazione antiorario (inverso al movimento
delle lancette dell'orologio) come positivo.
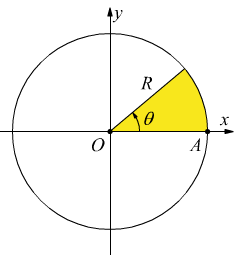
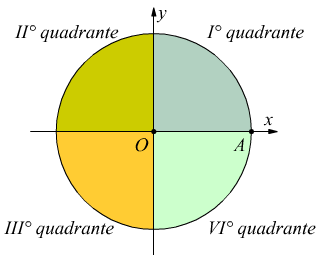
La convenzione, vuole che la circonferenza con centro nell'origine della coppia di assi cartesiani venga suddivisa in 4 zone chiamate quadranti, anche l'ordine di dispozizione dei quadranti segue la regola del senso antiorario come si vede nel disegno.
Gradi e radianti
Noi, usiamo frequentemente misurare l'ampiezza degli angoli secondo il sistema sessaggesimale da 0° a 360°
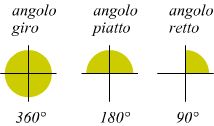
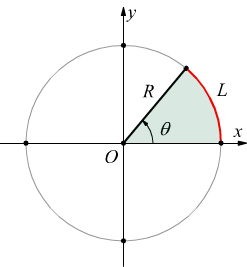
questa non è la misura ufficiale degli angoli; più rigorosamente un angolo deve essere misurato in radianti
$$θ_{rad}=L/R $$
L = lunghezza dell'arco di circonferenza sotteso all'angolo θ
R = raggio della circonferenza
questa definizione, nel caso della circonferenza trigonometrica con R=1, comporta che il valore dell'angolo in radianti coincida con il valore della lunghezza dell'arco sotteso dall'angolo stesso. Sappiamo che la lunghezza di una circonferenza è C=2πR. Quindi nella circonferenza trigonometrica (R=1):
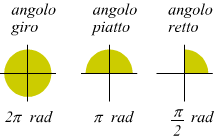
angolo giro = 2π radiandi
angolo piatto = π radianti
angolo retto = $$π/2$$ radianti
Questo quadro di cose non cambia anche se il cerchio non fosse a raggio unitario, perchè il rapporto $$L/R$$ non varia al variare della circonferenza ma dipende solo dall'angolo θ. E' dunque facile costruire la proporzione che lega tra loro gradi e radianti:
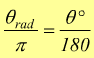
se conosciamo $θ°$ troviamo $$θ_{rad}=π/180⋅θ°$$
se conosciamo $θ_{rad}$ troviamo $$θ°=180/π⋅θ_{rad}$$
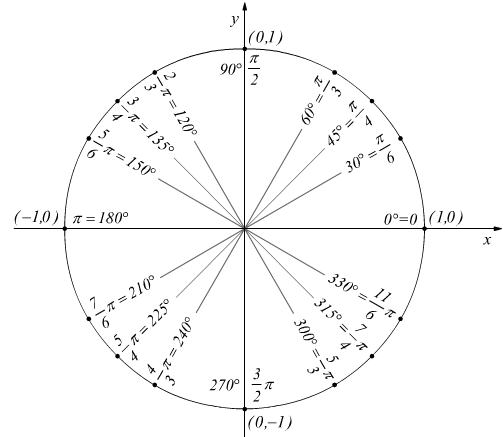
Gli angoli notevoli in gradi e radianti sono qui sotto rappresentati.
E'
anche disponibile un riassunto sul cerchio
trigonometrico.
Funzioni Trigonometriche
Su un piano cartesiano, costituito da due assi ortogonali, tracciamo una circonferenza di raggio R con centro nell'origine O della coppia di assi. Scegliamo arbitrariamente un punto P sul I° quadrante della circonferenza il raggio

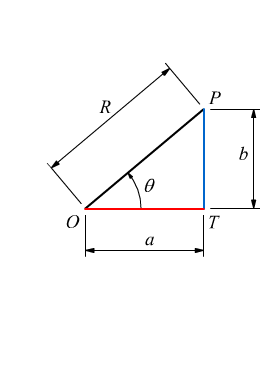
Il raggio R = OP determina un angolo θ con l'asse
x delle ascisse.
Definiamo il punto H come la proiezione ortogonale di P sull'asse y delle ordinate.
Definiamo il punto T come la proiezione ortogonale di P sull'asse x delle ascisse.
Potranno essere individuati i due segmenti:
a=OT=PH e b=OH=PT ,
definiamo:
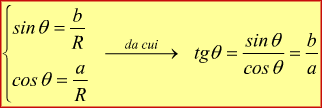
nel caso sia il raggio R=1 si riconosce che:
una circonferenza di raggio unitario (R=1) viene chiamata circonferenza trigonometrica o circonferenza goniometrica.
Variazioni del seno
Nel cerchio trigonometrico di raggio 1:
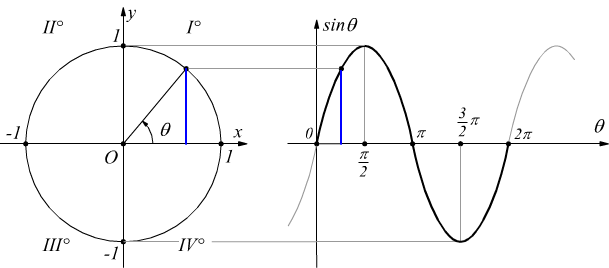
Se θ=0 si ha b=sinθ=0
Se immaginiamo che il punto P si muova lungo la circonferenza in sento antiorario (convenzionalmente positivo)
● Se 0°<θ<90° sinθ varia
da 0 a 1, il raggio del cerchio si trova nel I° quadrante con funzione sinθ
CRESCENTE.
● Se 90°<θ<180° sinθ varia
da 1 a 0, il raggio del cerchio si trova nel II° quadrante con funzione
sinθ DECRESCENTE.
● Se 180°<θ<270° sinθ varia
da 0 a -1, il raggio del cerchio si trova nel III° quadrante con funzione
sinθ DECRESCENTE.
● Se 270°<θ<360° sinθ varia
da -1 a 0, il raggio del cerchio si trova nel IV° quadrante con funzione
sinθ CRESCENTE.
Variazioni del coseno
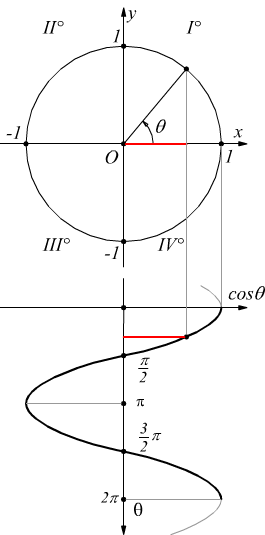
Nel cerchio trigonometrico di raggio 1: se θ =0 si ha a=cosθ =1.
Se immaginiamo che il punto P si muova lungo la circonferenza in sento antiorario (convenzionalmente positivo)
● Se 0°<θ <90° cosθ varia da 1 a 0, il raggio del cerchio si trova nel I° quadrante con funzione cosθ DECRESCENTE.
● Se 90°<θ<180° cosθ varia da 0 a -1, il raggio del cerchio si trova nel II° quadrante con funzione cosθ DECRESCENTE.
● Se 180°<θ <270° cosθ varia da -1 a 0, il raggio del cerchio si trova nel III° quadrante con funzione cosθ CRESCENTE.
● Se 270°<θ <360° cosθ varia da a 1, il raggio del cerchio si trova nel IV° quadrante con funzione cosθ CRESCENTE.
Variazioni della tangente
Sul cerchio trigonometrico di raggio 1 conduciamo ad esso la tangente nel punto A; chiamiamo B l'intersezione fra la retta tangente h e il prolungamento del raggio R passante per P. Per la similitudine dei triangoli:
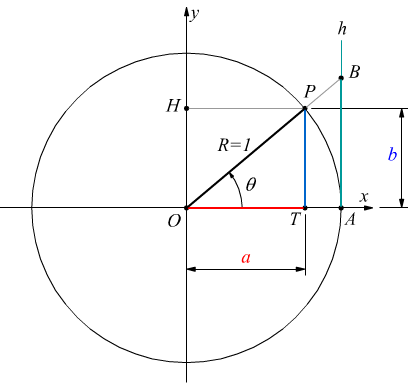

essendo R=1 si ha AB=tgθ
Se immaginiamo che il punto P si muova lungo la circonferenza in senso antiorario (convenzionalmente positivo) si potrà ottenere il seguente grafico
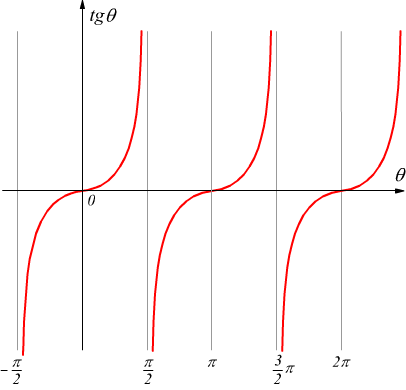
● Per 0°<θ<90° il punto P ed il raggio R si trovano nel I° quadrante; il punto B descrive la parte positiva della retta h andando da AB=0 per θ=0 ad AB=+∞ per $$θ=π/2=90°$$ la funzione tgθ è CRESCENTE.
● Per 90°<θ<180° il punto P ed il raggio R si trovano nel II° quadrante; il punto B descrive la parte negativa della retta h andando da AB=-∞ per $$θ=90°=π/2$$ ad AB=0 per θ=π=180° la funzione è tgθ CRESCENTE.
● Per 180°<θ<270° il punto P ed il raggio R si trovano nel III° quadrante; B si comporta come nel I° quadrante (descrive la parte positiva della retta h) andando da AB=0 per θ=π=180° ad AB=+∞ per $$θ=3/2π=270°$$ la funzione tgθ è CRESCENTE.
● Per 270°<θ<360° il punto P ed il raggio R si trovano nel IV° quadrante; B si comporta come nel II° quadrante (descrive la parte negativa della retta h) andando da AB=-∞ per $$θ=3/2π=270°$$ ad AB=0 per θ=2π=360° la funzione tgθ è CRESCENTE.
Funzione inversa arcoseno
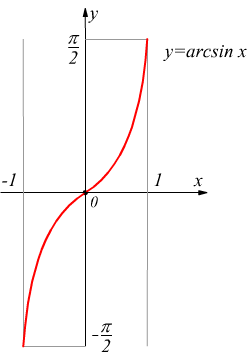
Dati i numeri reali x ed y con -1 ≤ x ≤ 1 ed $$-π/2 ≤ y ≤ π/2$$ si ha la funzione inversa
$y=arcsinx$ con dominio D=[-1; 1] e codominio C=$$[-π/2; +π/2]$$
se appunto $x=siny\;\;⟶\;\;y=arcsinx$
Funzione inversa arcocoseno
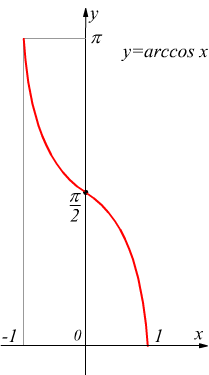
Dati i numeri reali x ed y con -1 ≤ x ≤ 1 ed 0 ≤ y ≤ π si ha la funzione inversa
$y=arccosx$ con dominio D=[-1; 1] e codominio C=[0; π]
se appunto $x=cosy\;\;⟶\;\;y=arccosx$
Funzione inversa arcotangente
Dati i numeri reali x ed y con x ∈ R ed $$-π/2≤y≤π/2 $$ si ha la funzione inversa
$y=arctgx$ con dominio D ≡ R e codominio C=$$]-π/2;π/2[$$
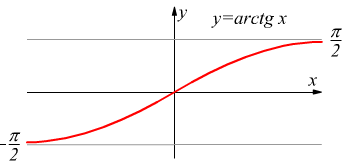
se appunto $x=tgy\;\;⟶\;\;y=arctgx$
Funzioni reciproche
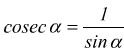
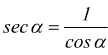
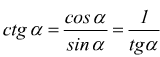
con limitazioni -1 ≤ sinα ≤ 1 e -1 ≤ cosα ≤ 1
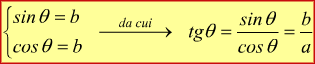
Relazione fondamentale della trigonometria
La relazione fondamentale della trigonometria può essere facilmente dedotta applicando il teorema di Pitagora al cerchio goniometrico.
![]()
Relazioni tra funzioni goniometriche
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Archi associati
Angoli complementari
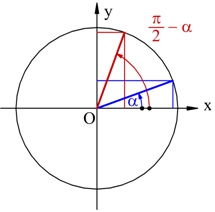
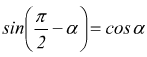
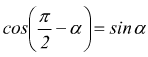
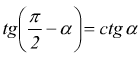
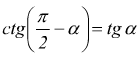
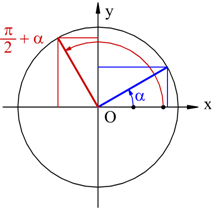
Angoli che differiscono di un angolo retto
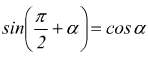
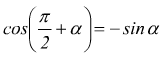
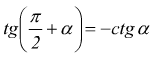
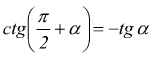
Angoli che hanno per somma tre angoli retti
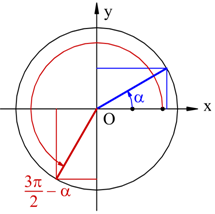
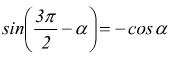
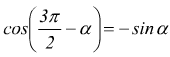
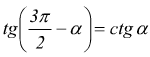
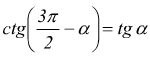
Angoli che differiscono di tre angoli retti
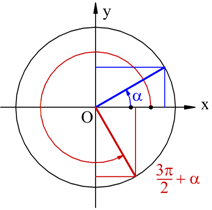
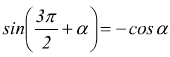
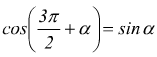
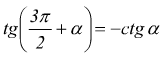
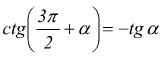
Angoli che differiscono di un angolo piatto
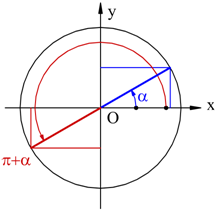
![]()
![]()
![]()
![]()
Angoli supplementari
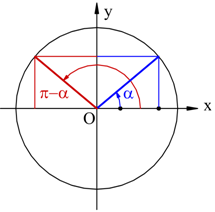
![]()
![]()
![]()
![]()
Angoli esplementari
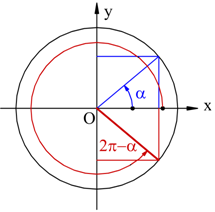
![]()
![]()
![]()
![]()
Angoli opposti
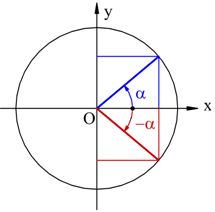
![]()
![]()
![]()
![]()
Formule di addizione e sottrazione
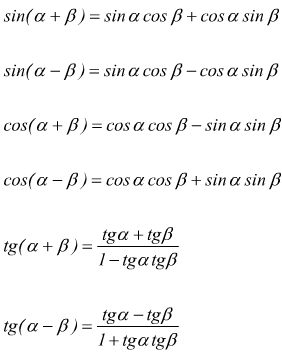
Formule di duplicazione
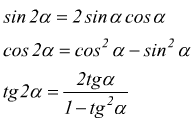
Formule di bisezione
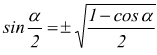
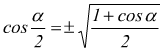
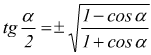
Formule di parametriche
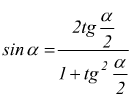
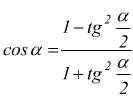

con ![]()
Formule di Werner
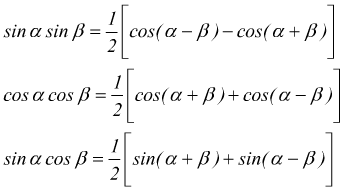
Formule di prostaferesi
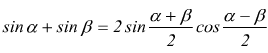
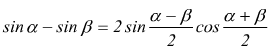
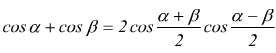
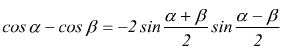
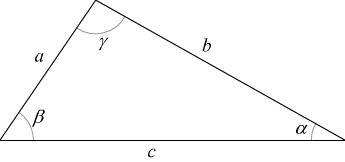
Teorema dei seni
Il teorema dei seni afferma che in un triangolo qualsiasi le misure di due lati stanno tra loro come i seni degli angoli opposti.

Teorema delle proiezioni
![]()
![]()
![]()
Teorema di Carnot
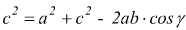
Formule di Briggs
con p=semiperimetro del triangolo
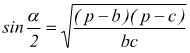 |
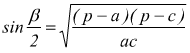 |
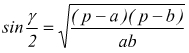 |
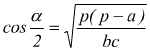 |
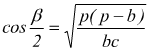 |
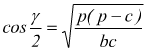 |
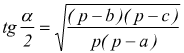 |
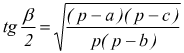 |
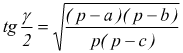 |
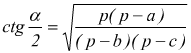 |
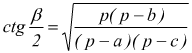 |
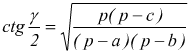 |
Angoli particolari
|
gradi |
radianti |
sin |
cos |
tg |
ctg |
|
0° |
0 |
0 |
1 |
0 |
$∄$ |
|
30° |
$$π/6$$ |
$$1/2$$ |
$$√3/2$$ |
$${√3}/3$$ |
$${√3}$$ |
|
45° |
$$π/4$$ |
$$√2/2$$ |
$$√2/2$$ |
1 |
1 |
|
60° |
$$π/3$$ |
$$√3/2$$ |
$$1/2$$ |
$$√3$$ |
$$√3/3$$ |
|
90° |
$$π/2$$ |
1 |
0 |
$∄$ |
0 |
|
180° |
$π$ |
0 |
- 1 |
0 |
$∄$ |
|
270° |
$$3/2π$$ |
-1 |
0 |
$∄$ |
0 |
|
360° |
$2π$ |
0 |
1 |
0 |
$∄$ |
 edutecnica
edutecnica