Integrale di superficie

Consideriamo la funzione

Si tratta di una funzione a tre variabili x,y,z quindi, ad ogni terna di queste variabili corrisponde un solo valore di t.

I campi di esistenza di una funzione di questo tipo sono generalmente volumi o aree di superfici di solidi, dato che le terne x,y,z descrivono punti nello spazio tridimensionale.

Ad es. se diciamo che la precedente funzione è definita per x²+y²+z² ≤ R² vuol dire che la funzione assegnata acquista valori determinati in ogni punto interno della sfera di raggio R (e sulla sua superficie).

Allo stesso modo se diciamo che la T(x,y,z) è definita per x²+y²+z² = R² vuol dire che essa acquista valori determinati in ogni punto della superficie della sfera di raggio R.

Se diciamo che la T(x,y,z) è una funzione definita e continua nei punti di superficie S di equazione F(x,y,z)=0 significa che per ogni terna x,y,z che soddisfa la F(x,y,z)=0 (punti della superficie S) la T(x,y,z) risulta definita e continua.

La T(x,y,z) è dunque funzione dei punti P appartenenti ad S tali che t=T(P).

Supponendo di esplicitare la F(x,y,z) rispetto a z, cioè che l'equazione di S sia z=f(x,y)
La funzione T[x,y,f(x,y)] che ne deriva, è funzione delle sole variabili x,y ed il suo campo di definizione è quello della z=f(x,y) cioè il dominio D del piano x,y che si ottiene proiettando la superficie S sul piano x,y.

Supponendo di esplicitare la F(x,y,z) rispetto a z, cioè che l'equazione di S sia z=f(x,y)

La funzione T[x,y,f(x,y)] che ne deriva, è funzione delle sole variabili x,y ed il suo campo di definizione è quello della z=f(x,y) cioè il dominio D del piano x,y che si ottiene proiettando la superficie S sul piano x,y.

Versore normale ad una superficie

Un punto P di una superficie di equazione F(x,y,z)=0 è denominato punto semplice se in esso esistono e sono continue le sue tre derivate parziali prime

Se le tre derivate parziali sono nulle, o almeno una non esiste il punto P è detto punto singolare.
Per ogni punto P appartenente alla superficie S (P∈S) passano infinite curve giacenti su S. Si considera dunque la generica superficie S di equazione

(I)

ed una delle sue infinite curve passanti per un suo punto semplice P di equazioni parametriche

(II)

E' possibile dimostrare che il vettore

valutato in ogni punto di S, è ortogonale ad ogni curva passante per P, quindi perpendicolare ad S.

Consideriamo il vettore ; può essere descritto in forma parametrica

derivando si ottiene

Moltiplichiamo scalarmente i vettori

Questo prodotto scalare è nullo, infatti sostituendo le (II) nella (I)

derivando membro a membro rispetto a t

Il prodotto scalare tra due vettori non nulli è nullo quando i due vettori sono perpendicolari.

Essendo tangente alla curva in P, il vettore deve essere perpendicolare a quella curva.

Se si ripete il ragionamento per tutte le curve passanti per P si deduce che è normale alle tangenti a tutte le curve passanti per il punto e per definizione è perpendicolare alla superficie nello stesso punto.

Nella notazione, che usiamo, sono i tre versori degli assi x,y,z. Si ha quindi

Vengono poi definiti i coseni direttori, cioè i coseni degli angoli formati da coi tre assi cartesiani.

dove deve essere interpretato come il versore di (cioè il vettore di modulo 1 che ha lo stesso verso e direzione di ). Formalmente definito come:

Se l'equazione che descrive la superficie S è espressa come

si ha 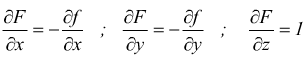dunque

è orientato in modo tale da formare sempre un angolo acuto (al più retto) con l'asse z

Nel caso in cui si abbia

si ha dunque

dall'ultima equazione si deduce che è orientato in modo tale da formare sempre un angolo ottuso (al più retto) con l'asse z

Calcolo dell'integrale di superficie

Sono chiamati integrali di superficie gli integrali doppi estesi ad una porzione di superficie curva cioè:

In questa formula S è una superficie curva mentre dS è l'elemento infinitesimo di superficie, cioè una porzione di superficie curva S tanto piccola da poter essere considerata piana.T(x,y,z) si sottintende come funzione continua.

Supponiamo che la superficie abbia equazione z=f(x,y) definita e continua in tutti i punti del dominio D proiezione di S sul piano xy. Nel dominio D prendiamo un elemento infinitesimo dσ=dxdy; se questo viene proiettato su S si ottiene l'elemento dS. Se è il versore normale a dS in un punto P ∈S la relazione tra ds e dxdy è

se l'angolo tra e il versore per l'asse z è acuto.