Scomposizione di polinomi

Scomporre un polinomio in fattori significa trasformare un polinomio, che è normalmente rappresentato da una somma algebrica di monomi, nel prodotto di altri polinomi di grado inferiore a quello del polinomio assegnato inizialmente. Tra i fattori ottenuti può esserci anche un monomio.
Questa operazione viene talvolta chiamata fattorizzazione o riduzione in fattori di un polinomio.

La scomposizione di un polinomio in fattori è una operazione del tutto analoga alla scomposizione in fattori di un numero naturale.

Scomporre in fattori un numero significa scriverlo come prodotto di altri numeri

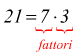
7·3 è una scomposizione in fattori di 21.

Scomporre in fattori un polinomio significa scriverlo come prodotto di altri polinomi

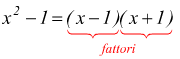
(x-1)(x+1) è una scomposizione in fattori di x²-1

Se non è possibile scomporre un polinomio in fattori, questo polinomio viene chiamato irriducibile; in caso contrario esso è detto riducibile.

Polinomi riducibili

Il binomio x²-9 è riducibile perchè, per le regole dei prodotti notevoli:

entrambi i fattori della scomposizione hanno grado 1; la somma dei gradi dei due polinomi ottenuti fa 2 che è il grado del polinomio assegnato.

Il binomio x³+x² è riducibile perchè è possibile riscriverlo come

il primo fattore della scomposizione ha grado 2, il secondo ha grado 1 la somma fa 3 che è il grado del polinomio assegnato imizialmente.

Polinomi irriducibili

Il binomio 4x+3 è irriducibile; non può essere scomposto nel prodotto di fattori di grado inferiore, ossia di grado zero anche perchè il prodotto di numeri (polinomi di grado 0) non può dar luogo ad un binomio di grado 1. (0+0≠1) .

Il binomio x²+1 è irriducibile; infatti, ammettiamo, per ipotesi che esso possa essere ottenuto come prodotto tra due binomi di primo grado

si nota, che mentre il primo membro (x²+1)>1 per ogni valore di x, il secondo membro si può annullare per $$x=-d/c$$ e questo fatto è impossibile.

Il problema di come ridurre un polinomio in fattori, dipende da quale insieme numerico si vuole che appartengano i coefficienti dei polinomi fattori.
Un matematico esperto, direbbe che x²+1 può essere scomposto in fattori con coefficienti appartenenti al campo dei numeri complessi (C).

Il binomio (x²-2) è scomponibile invece nel campo dei numeri irrazionali

Anche con queste restrizioni, è possibile osservare che c'è una certa analogia tra i polinomi ed i numeri.

Teorema fondamentale dell’aritmetica

Ogni numero naturale maggiore di 1 o è primo oppure è composto; cioè, può essere scritto come prodotto di numeri primi.

Teorema di scomponibilità dei polinomi

Ogni polinomio a coefficienti reali o è irriducibile oppure può essere scritto come prodotto di fattori irriducibili.

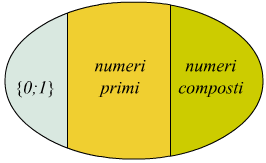
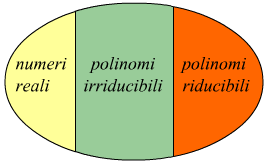
Si nota come i polinomi irriducibili nell’insieme dei polinomi,abbiano lo stesso ruolo dei numeri primi nell’insieme dei numeri naturali.

Tecniche di scomposizione di polinomi

Scomporre un polinomio non è un lavoro che può essere sottovalutato, infatti, mentre nel caso dei numeri interi la riduzione in termini primi diventa difficoltosa solo quando i numeri diventano piuttosto grandi, nel caso dei polinomi possono insorgere difficoltà ardue anche quando il grado del polinomio è basso.
In generale ci si affida a diversi metodi alternativi che risultano più o meno convenienti a secondo dei casi particolari.

Raccoglimento totale

Il modo più semplice per scomporre un polinomio in fattori, consiste nel mettere in evidenza i fattori comuni a tutti i termini del polinomio.
Questa tecnica di scomposizione è chiamata raccoglimento a fattor comune o anche raccoglimento totale, che può essere fatta quando tutti i termini del polinomio hanno in comune un monomio.
Il raccoglimento totale è basato sulla proprietà distributiva della moltiplicazione rispetto all'addizione.
Se indichiamo con A,B e C tre monomi qualsiasi nell'espressione AB+AC, notiamo come il monomio in comune sia A:

con quest'ultima scrittura si indica che il polinomio AB+AC è stato decomposto nel prodotto di due fattori: il monomio A ed il polinomio B+C. E' stato messo in evidenza, in questo caso, il monomio A, fattore comune ai termini del polinomio AB+AC. Se volessimo scomporre il polinomio 2x²+6xy scriveremmo

l'operazione eseguita è evidente

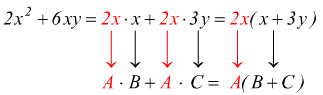
Il polinomio da scomporre può anche essere trinomio, quadrinomio, ad es.

20x⁴+30x²y³-40x³y

NOTA:si cerca sempre di mettere in evidenza quello che è l'MCD di tutti i termini che appaiono

MCD(20x⁴,30x²y³,40x³y)=10x² anche se spesso il termine da raccogliere è visibile ad occhio.

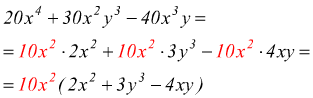
Quando il termine di grado massimo di un polinomio ha coefficiente negativo, è cosigliabile raccogliere un fattore con coefficiente negativo, come nel caso di -3x³+9x² è più utile raccogliere -3x² che 3x² ottenendo

in questo modo il fattore (x-3) di grado massimo risulta avere un coefficiente positivo.

Nei casi precedenti il fattore comune raccolto era un monomio;a volte è più utile raccogliere un polinomio senza svolgere tutte le moltiplicazioni che si sarebbe tentati di fare, come nel caso di $x(a-b)-3y(a-b)$.

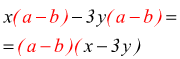
Raccoglimento parziale

Può accadere che , in prima battuta, che non sia possibile effettuare un raccoglimento totale in un polinomio, perchè ci sono dei fattori comuni solo in certi gruppi di termini; ma può accadere che dopo aver raccolto in questi gruppi i rispettivi fattori comuni sia possibile in seguito un raccoglimento totale.
In questi casi si parla di raccoglimento parziale di fattori comuni. Ad es.

si può dapprima mettere in evidenza nei primi due termini la x e nei secondi due la y.

per poi raccogliere il fattore comune (a+b).

molti polinomi possono essere scomposti come si è visto, eseguendo prima dei raccoglimenti parziali e poi dei raccoglimenti totali.
Non ci sono delle regole fisse per scegliere i termini sui quali effettuare il raccoglimento parziale ma la strategia è sempre quella: i raccoglimenti parziali vanno effettuati in modo da permettere in seconda battuta un raccoglimento totale.

Ad es. x⁴-x³-x+1 sui primi due termini si può raccogliere a fattor comune x²:

Ad es. 6a²-3ab-10a+5b

Ad es. x²y+xy²+x+y

Scomposizione mediante prodotti notevoli

La possibilità di scomporre un polinomio mediante i prodotti notevoli è totalmente legata alla capacità di riconoscere e ricondurre un'espressione ad uno specifico prodotto notevole. Ad es.

Differenza di quadrati A²-B²=(A-B)(A+B)

Quadrato di un binomio A²+2AB+B²=(A+B)²

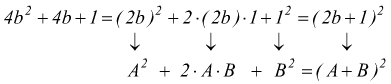
Queste regole possono essere applicate anche nel caso di tutti gli altri prodotti notevoli, cioè, cubo di un binomio, quadrato di un trinomio, somme e differenze di cubi, etc..

Scomposizione con la regola di Ruffini

Il teorema di Ruffini, può essere usato opportunamente per cercare di scomporre in fattori un generico polinomio N(x) determinando i binomi del tipo (x-a) per i quali N(x) è divisibile. In modo da rappresentare N(x)=(x-a)·Q(x).
Questo accade, come sappiamo, se risulta N(a)=0. Il problema viene quindi ricondotto alla ricerca di quei valori di a per i quali N(a)=0.
Essi vengono chiamati radici o zeri del polinomio N(x). Si tratta, quindi, di andare a tentativi .

In generale non è detto che un polinomio abbia sempre una radice e poi anche nel caso che questa esista, non sempre è facile determinarla.
Noi, comunque, ci limitiamo solo ai casi più semplici, cioè, alla ricerca di zeri interi di polinomi a coefficienti interi; affidandoci al seguente criterio.

Zeri interi di un polinomio a coefficienti interi :
Gli eventuali zeri interi (non nulli) di un polinomio a coefficienti interi, sono da ricercare tra i divisori, positivi o negativi, del termine noto del polinomio.

Ad es. dato il polinomio N(x)=x³-x-6

le eventuali radici intere si devono ricercare, per tentativi, tra i divisori, positivi e negativi, del termine noto -6, cioè tra i numeri ±1, ±2, ±3, ±6

N(1)=-6≠0	N(-1)= -6≠0
N(2)=0	N(-2)=-12≠0
N(3)=18≠0	N(-3)=-30≠0
N(6)=204≠0	N(-6)=-216≠0

Si vede come solo N(2)=0, quindi l'unica radice intera del polinomio è 2.
Per il teorema di Ruffini se N(2)=0, N(x) è divisibile per (x-2) e poi troviamo il quoziente Q(x) attraverso lo schema di Ruffini:

Ora possiamo scrivere

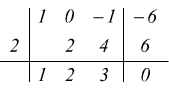
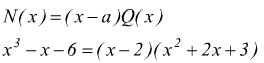
Ovviamente, si può tentare di cercare di ridurre ulteriormente il polinomio quoziente; questo può avvenire applicando il metodo appena esposto allo stesso Q(x). Se, come in questo caso, Q(x) è un polinomio di secondo grado, risulterà sempre più conveniente applicare la formula risolutiva del trinomio di secondo grado, sempre che il prof. ci permetta di usarla, altrimenti dobbiamo scomporre il trinomio di secondo grado, ancora con la regola di Ruffini.

Riassumendo

1.) cerchiamo se tra i divisori, positivi o negativi, del termine noto N(x), c'è qualche zero di N(x)

2.) non appena troviamo uno zero lo chiamiamo a, eseguiamo la divisione del polinomio dato N(x) per (x-a) secondo lo schema di Ruffini: chiameremo Q(x) il quoziente della divisione

3.) scriviamo la scomposizione del polinomio N(x)=(x-a)·Q(x) ed eventualmente procediamo a scomporre ulteriormente Q(x), ammesso che esso sia ancora riducibile.

Si può andare un poco oltre il criterio appena esposto, considerando anche la ricerca di radici razionali del polinomio assegnato, sempre ammettendo che questo abbia solo coefficienti interi:

Dato un polinomio N(x) a coefficienti interi, le eventuali radici razionali del polinomio sono da ricercarsi tra le frazioni aventi per numeratore un divisore (positivo o negativo) del termine noto e per denominatore un divisore (positivo o negativo) del coefficiente di grado massimo (primo coefficiente del polinomio dopo che esso è stato ordinato secondo le potenze decrescenti della variabile).

Ad es. vogliamo scomporre N(x)=6x²+x-1

Le eventuali radici intere potrebbero essere solo ±1 ma per questi valori il polinomio non si annulla, come si può verificare.
A questo punto tentiamo di vedere se è possibile individuare la presenza di eventuali radici razionali che sono da ricercarsi tra i valori

`+-1/6 +-1/2 +-1/3` si trova

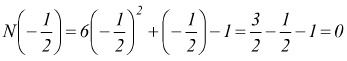
quindi il polinomio è divisibile per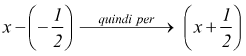

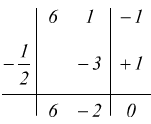
ottenendo Q(x)=6x-2 dunque la scomposizione effettuata

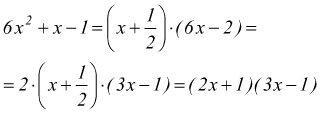
La prospettiva di eseguire la fattorizzazione di un polinomio andando per tentativi non è mai molto entusiamante; ragion per cui, un paio di regole supplementari possono essere utili.

I.) Quando la somma dei coefficienti di N(x) è uguale a zero, il numero 1 è senz'altro una radice del polinomio. Infatti N(1) risulta sempre essere uguale alla somma dei coefficienti.
Ad es. ipotizzando N(x)=8x³+17x-25 prevede che sia 8+17-25=0 dunque 1 è una radice del polinomio; infatti
8·1³+17·1-25=8+17-25=0
il polinomio assegnato è divisibile per (x-1).

II.) Quando la somma dei coefficienti di grado pari del polinomio N(x)è uguale alla somma dei coefficienti dei termini di grado dispari, allora il numero -1 èuna radice del polinomio. Infatti N(-1) risulta uguale alla somma dei coefficienti dei termini di grado pari meno la somma dei coefficienti dei termini di grado dispari.
Ad es. ipotizzando N(x)=2x⁴+8x³+4x²+3x+5 notiamo come sia 2+4+5=8+3 come detto, in questo caso -1 deve essere una radice.
N(-1)=2·(-1)⁴+8·(-1)³+4·(-1)²+3·(-1)+5= =2-8+4-3+5=0
il polinomio assegnato è divisibile per x-(-1) → (x+1).

Il seguente modulo "tenta" di scomporre un polinomio a coefficienti interi nella variabile x, inserito in input con notazione ASCIImath (+-*/^ come in Excel):