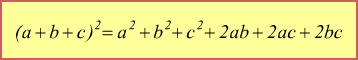Prodotti notevoli
In algebra, è ricorrente e molto frequente imbattersi in moltiplicazioni tra particolari polinomi che possono essere eseguite seguendo le normali regole del calcolo letterale con dei risultati che hanno una forma caratteristica e facilmente memorizzabile. Questi particolari prodotti vengono chiamati prodotti notevoli.
quadrato della somma di due monomi
quadrato della differenza di
due monomi
Prodotto della somma di due monomi per la loro differenza
cubo di un binomio, somma di due monomi
cubo di un binomio,
differenza di due monomi
Vi sono, inoltre, altre identità algebriche notevoli, come le seguenti
Quadrato di un binomio
Quadrato della
somma di due monomi : Assegnati due generici monomi: a
e b la loro somma è $a+b$.
Per definizione di potenza è:
si conclude che
Il quadrato di un binomio, somma di due monomi, è uguale al quadrato del primo monomio, più il doppio del primo monomio per il secondo, più il quadrato del secondo monomio.
Quadrato della differenza di due monomi : Se invece consideriamo la differenza dei due monomi, cioè : $a-b$
si conclude che
Il quadrato di un binomio, differenza di due monomi, è uguale al quadrato del primo monomio, meno il doppio del primo monomio per il secondo, più il quadrato del secondo monomio.
esempio A:
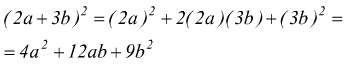
esempio B:
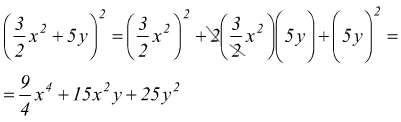
esempio C:
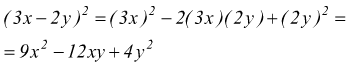
Si possono presentare casi particolari come $(-a-b)^2$ ma si risolvono facilmente applicando le regole del calcolo letterale vista finora.
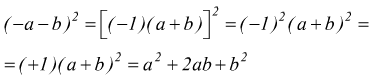
nel caso il monomio si presenti nella forma $(-a+b)^2$ si procede come prima
esempio D:
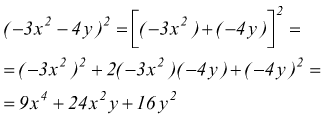
esempio E:
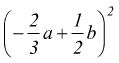può
essere riscritta come
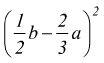poi
si applica la formula $(a-b)^2=a^2-2ab+b^2$
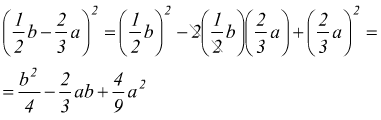
Quadrato di un trinomio
Il quadrato di un trinomio è uguale alla somma dei quadrati dei singoli termini, più i doppi prodotti di ciascun termine per quelli che seguono.
ci si può ricordare di questa formula, semplicemente eseguendo il calcolo
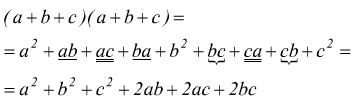
esempio F:
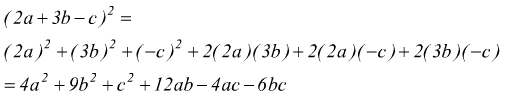
esempio G:
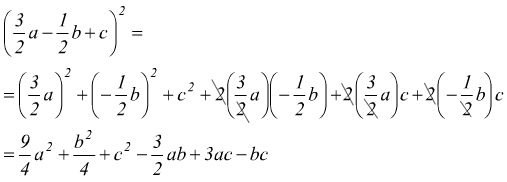
Prodotto della somma di due monomi per la loro differenza
Il prodotto della somma di due monomi per la loro differenza è uguale al quadrato del primo monomio meno il quadrato del secondo.
Eseguendo la moltiplicazione con le regole normali si ha:
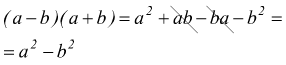
esempio H: eseguire l'operazione 
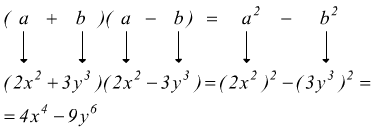
esempio I:
esempio L: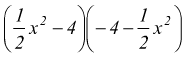 
è
possibile eseguire il raccoglimento di (-1) nel secondo binomio
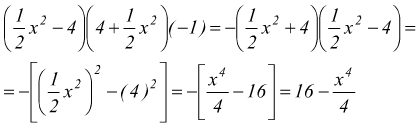
esempio M: 
poniamo
a=x+y e b=2z
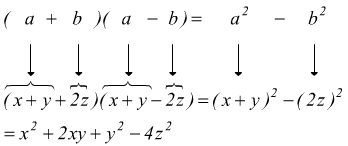
Cubo di un binomio
Il cubo di un binomio, somma di due monomi è uguale al cubo del primo termine più il triplo prodotto del quadrato del primo termine per il secondo, più il triplo prodotto del primo per il quadrato del secondo, più il cubo del secondo.
Infatti
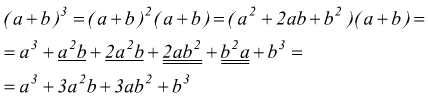
Il cubo di un binomio, differenza di due monomi, è uguale al cubo del primo termine, meno il triplo prodotto del quadrato del primo termine per il secondo, più il triplo prodotto del primo per il quadrato del secondo, meno il cubo del secondo termine.
Somma e differenza di cubi
Sempre utilizzando i due monomi a e b, prendiamo in considerazione il seguente prodotto
sviluppando
il prodotto con le solite regole si ha
in
pratica
somma
di due monomi al cubo
se in questa formula si sostituisce -b a b si ottiene
differenza
di due monomi al cubo
i due termini $(a^2±ab+b^2)$ sono chiamati falsi quadrati ; essi non sono il quadrato di $(a±b)$ e non sono ulteriormente scomponibili (sono irriducibili).
esempio N: sviluppare la seguente somma
di monomi al cubo $8x^3+27y^3$
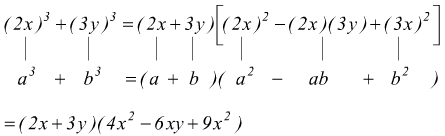
esempio O:
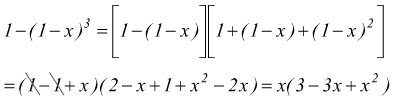
esempio P:
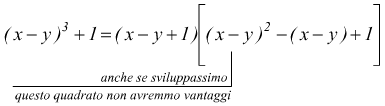
Trinomio notevole
Un trinomio del tipo $x^2+(a+b)x+ab$
cioè un trinomio di secondo grado in una variabile, in cui il primo coefficiente è uguale a 1, il secondo coefficiente è la somma di due numeri, il cui prodotto è uguale al termine noto può essere trasformato nel seguente modo
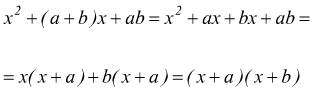
quindi si ha la scomposizione
In generale, perché un polinomio di secondo grado che abbia il coefficiente del termine di secondo grado uguale a 1, si possa trasformare in un prodotto con la regola appena vista, bisogna che il coefficiente di primo grado si possa scomporre nella somma di due numeri, il cui prodotto sia uguale sia uguale al termine noto (termine di grado zero).
Esempio P: scomporre in fattori il polinomio $x^2+5x+6$
dobbiamo vedere se esistono due numeri la cui somma sia 5 ed il prodotto
6; questi due numeri esistono e sono 2 e 3
Esempio Q: scomporre
$a^2-7a+10$
in questo caso i due numeri che danno per somma -7 e per prodotto 10 sono
-2 e -5
Esempio R: scomporre in fattori il polinomio
$x^2+2ax-15a^2$
dobbiamo trovare due numeri la cui somma è 2a ed il prodotto -15a2
questi due numeri sono 5a e -3a.
Potenze successive di un binomio
Se volessimo
trovare una formula generale per lo sviluppo del binomio $(a+b)^n$
con $n∈N$ dovremmo partire dai dati già in nostro possesso
$(a+b)^0=1$
$(a+b)^1=a+b$
$(a+b)^2=a^2+2ab+b^2$
$(a+b)^3=a^3+3a^2b+3ab^2+b^3$
potremmo anche continuare ad aumentare l'esponente del binomio
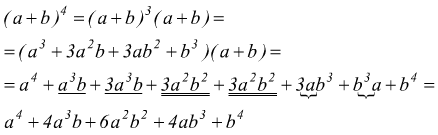
si riconosce che gli sviluppi fin qui effettuati rispettano una struttura
1.) ogni sviluppo ha un termine in più rispetto al precedente;
2.) i coefficienti dei termini estremi e di quelli equidistanti dagli estremi
sono identici;
3.) lo sviluppo di (a+b)n contiene n+1 termini, il primo è an
e l'ultimo è bn;
4.) se a e b sono monomi di primo grado, ogni sviluppo è un polinomio omogeneo
di grado n, completo sia ripetto alla lettera a che alla lettera b, ordinabile
secondo potenze decrescenti di a e potenze crescenti di b.
Proviamo a disporre i coefficienti degli sviluppi fin qui trovati, secondo una schema triangolare:
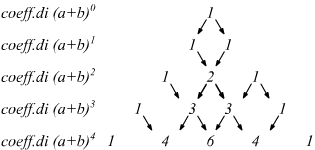
Dalle frecce si può vedere evidenziata la legge di formazione di questo triangolo: i numeri di ciascuna riga, dalla terza in poi, si ottengono (tranne il primo e l'ultimo che sono sempre uguali a 1) sommando i due della riga superiore.
Proseguendo nella costruzione di questo schema si ottiene il triangolo di Tartaglia.
Basandoci su questa struttura, si possono allora, ottenere i successivi sviluppi; ad es.
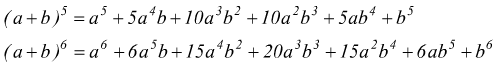
e così via.
Notiamo poi, dato che è
lo sviluppo del binomio (a-b)n si ottiene da quello di (a+b)n
sostituendo -b al posto di b ed in questo caso i
segni dei termini dello sviluppo risultano alternati ; quindi:
Come si può verificare