Calcolo percentuale
In matematica, la nozione di percentuale è strettamente legata al concetto di proporzione, ma se qualcuno ci chiedesse cosa sia una percentuale potremmo rispondere nel seguente modo:
Una percentuale è un rapporto che ha come conseguente 100 e come antecedente un numero intero o decimale.
In altri termini si potrebbe dire che una percentuale è una frazione che ha come denominatore 100 e come numeratore un numero intero o decimale.

Per rappresentare una percentuale si scrive l’antecedente del rapporto (il numeratore della frazione) seguito dal simbolo % (per cento).
Il numeratore della frazione o l’antecedente del rapporto vengono indicati col simbolo r e chiamati tasso percentuale.
Si tratta dunque di rappresentazioni equivalenti.

In pratica è possibile indicare una percentuale in diversi modi; cioè come
| Percentuale |
75%
|
| Rapporto |
75:100
|
| Frazione in centesimi |
75
100
|
| Frazione ridotta ai minimi termini |
3
4
|
| Numero decimale |
0,75
|
Di fatto le percentuali si applicano sempre rispetto a una certa grandezza cioè descrivono una quantità rispetto a un'altra, quindi tipicamente si dice che

D'ora in poi indichiamo la parte con p e il
totale con T.
Per risolvere i problemi di calcolo percentuale si può sempre applicare
la seguente proporzione:
tasso:100=parte:totale
che con i simboli si scrive
![]()
oppure in forma frazionaria

In pratica, per trovare delle percentuali, occorre risolvere proporzioni in cui uno dei termini è sempre il 100.
Esempio : calcolo della parte.
S se in una scuola con 320 alunni ne sono stati promossi l'85% è evidente
che il totale è T=320 mentre il tasso percentuale r=85. Per trovare l'effettivo
numero degli alunni promossi, cioè la parte, scriveremo:

gli alunni promossi sono 272.
Esempio : calcolo del tasso percentuale.
Calcolare la percentuale dei promossi di una classe scolastica sapendo che
dei 24 studenti iscritti solo 18 sono stati promossi.
In questo caso conosciamo il totale T=24 e la parte p=18 non ci resta che
calcolare il tasso percentuale r.

dunque la percentuale dei promossi è del 75%.
Esempio : calcolo del totale
Il 40% di un numero è 20. Qual'è il numero?
In questo caso abbiamo il tasso r=40, e la parte p=20 mentre cerchiamo
il totale T. Impostiamo la proporzione:

Possono esistere percentuali anche più grandi del 100%. In questo caso,
la parte (percentuale) è più grande del totale.
Esempio: calcolo della parte (più grande del totale)
Calcola il 120% di 15.
In questo caso r=120 e T=15, dobbiamo trovare la p.

e si dice che il 120% di 15 è 18.
Aumento e diminuzione percentuale
Se una grandezza cambia valore la variazione assoluta è la differenza tra il suo valore finale e quello iniziale. La variazione percentuale è la variazione assoluta rispetto al valore iniziale.
Se una grandezza aumenta. la sua variazione è un numero positivo mentre se diminuisce la sua variazione è un numero negativo.
In questo tipo di calcolo percentuale la parte p deve essere espressa come la differenza tra la parte finale pf e la parte iniziale pi.
p=pf-pi
mentre il totale è costituito dalla parte iniziale pi cioè T=pi.
Esempio : Aumento di statura
Andrea era alto 115cm quando aveva 6 anni mentre oggi è alto 145cm. Di quanto
è aumentata la sua statura in percentuale?

Andrea ha avuto un aumento percentuale in altezza del 26% circa.
Esempio : aumento del guadagno
Un venditore ha guadagnato il mese scorso 1500€. Questo mese ha guadagnato
il 20% in più. Quanto ha guadagnato questo mese?
Si ha un aumento percentuale dunque r=20 è positivo. Il dato iniziale è
noto come pi=1500 il dato finale è invece incognito pf=?

che coincide col calcolare il 20% del valore iniziale  e
di sommarlo al valore iniziale pi.
e
di sommarlo al valore iniziale pi.
Comunque, questo mese, il venditore ha guadagnato 1800€.
Esempio : applicazione dell'IVA
Un tipico esempio di aumento percentuale è dato dall'applicazione dell'IVA
che attualmente è del 22%.
Supponiamo di voler comprare una asciugatrice che costa 312€+IVA. Quale
sarà il prezzo finale?
In questo caso r=22 positivo, mentre pi=312 con pf=?
Come nel caso precedente:

che coincide col calcolare il 22% del valore iniziale  e
di sommarlo al valore iniziale pi.
e
di sommarlo al valore iniziale pi.
Esempio : scorporo dell'IVA
Si tratta del problema opposto dell'applicazione dell'IVA.
Supponiamo di aver comprato un forno a microonde del prezzo di 280€. Quanto
è il suo costo IVA esclusa?
In questo caso pf=280 mentre pi=?

Esempio : diminuzione del prezzo
Un telefonino è stato pagato 126€ mentre appena uscito costava 180€. Di
quanto è diminuito il suo prezzo in percentuale?
Anche in questo caso cerchiamo il tasso percentuale r. sapendo che pi=180
e pf=126.

Il prezzo è diminuito del 30% .
Ovviamente in questa tipologia di problemi l'incognita può essere il valore finale pf o il valore iniziale pi della parte.
Esempio : diminuzione del peso
Una volpe, durante il letargo, perde il 25% del suo peso se all'inizio pesava
14kg quanto pesa alla fine del letargo?
Qui avremo r=-25 perchè si ha una diminuzione del valore iniziale, poi
abbiamo pi=14 mentre pf=?

alla fine del letargo la volpe peserà 10,5 kg.
Esempio : sconto
Un tipico esempio di diminuzione percentuale è lo sconto. Un commerciante
ha abbassato il prezzo di un certo articolo del 15% determinare il prezzo
originario di quell'articolo sapendo che l'attuale prezzo di vendita è di
102€.
Qui avremo r=-15 con pf=103 mentre pi=?

Il prezzo originario dell'articolo era di 120€.
Ricarico
Il ricarico nella terminologia economica restituisce il tasso percentuale di una grandezza che aumenta il suo valore, calcolato rispetto al suo valore iniziale pi. Esso è definito come:
 Ricarico
Ricarico
il tipico esempio di ricarico è dato dall'applicazione dell'IVA dove r=22 cioè si ha un ricarico del 22%.
Ad esempio un ricarico su un bene che costa 40€ e che viene venduto a 50€.

Margine
Il margine nella terminologia finanziaria restituisce il tasso percentuale di una grandezza che aumenta il suo valore, calcolato rispetto al suo valore finale pf. Esso è definito come:
 Margine
Margine
ad esempio un margine su un bene che costa 40€ e che viene venduto a 50€.
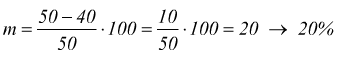
PF
 edutecnica
edutecnica