Rapporti
Si chiama rapporto tra due numeri presi in un certo ordine, il loro quoziente.
Ad esempio, se in una classe ci sono 11 maschi e 7 femmine :
il rapporto femmine/maschi è 7/11 mentre
il rapporto maschi/femmine è 11/7
Dunque, viene definito rapporto tra due grandezze omogenee, prese in un certo ordine, il quoziente tra le loro misure espresse nella stessa unità.
Ad esempio, il rapporto base-altezza (standard) per i monitor da computer è 4 a 3 e si scrive 4/3, anche se poi sappiamo che l'introduzione dei monitor per poter vedere i film in HD ha portato questo rapporto a 16/9.
rapporto b/h=16/9
questa uguaglianza può essere chiamata rapporto diretto; è possibile definire anche il rapporto inverso:
rapporto h/b=9/16



Viene definito rapporto inverso (di un dato rapporto) quello che si ottiene scambiando l'ordine delle grandezze considerate.
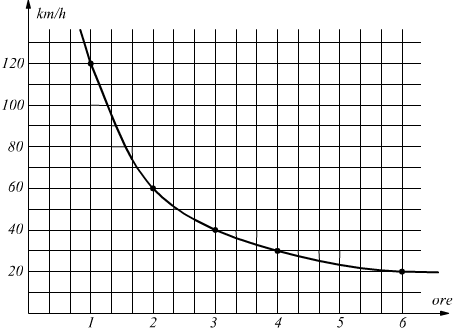
Si osserva poi, come il rapporto sia indipendente dall'unità di misura scelta

Nel disegno riportato si ha il
rapporto h/b=8/6=4/3
abbiamo, dunque, due frazioni equivalenti di cui solo 4/3 è ridotta ai minimi termini.
Un rapporto è semplificato quando è espresso da una frazione ridotta ai minimi termini:e' buona abitudine usare sempre rapporti semplificati.
b : 1
h : 1
Proporzioni
Una proporzione è un uguaglianza tra due rapporti.
Per esempio se
il bidone di vernice A ha un volume di 12 litri e costa 40€
il bidone di vernice B ha un volume di 15 litri e costa 50€
e leggeremo 12 sta a 15 come 40 sta a 50 ; questa è una proporzione . Questa scrittura può essere considerata anche in ordine inverso
15 : 12 = 50 : 40
e anche questa è una proporzione; i quattro numeri presenti in una proporzione sono chiamati termini.
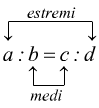
Il primo e l'ultimo termine sono chiamati estremi, il secondo ed il terzo termine sono chiamati medi.
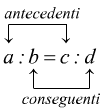
Il primo ed il terzo dermine si dicono antecedenti, mentre il secondo ed il quarto termine si dicono conseguenti.
Proprietà fondamentale delle proporzioni
In una proporzione, il prodotto dei medi è
uguale al prodotto degli estremi.
esempio:
3 : 5 = 9 : 15 → infatti è 5 · 9 = 3 · 15 in generale è:
Questa proprietà è molto importante. La nostra proporzione non è rappresentabile solo nella forma a : b = c : d ma anche in quella equivalente che prevede l'uso delle linee di frazione
le frazioni così ottenute sono uguali ed hanno lo stesso denominatore, di conseguenza devono essere uguali anche i numeratori cioè
a · d = b · c
Proprietà del permutare
• Una proporzione rimane valida se si scambiano tra loro i medi
a : b = c : d → a : c = b : d rimane invariata a · d = b · c
• Una proporzione rimane valida se si scambiano tra loro gli estremi.
a : b = c : d → d : b = c : a rimane invariata a · d = b · c
Proprietà dell'invertire
• Una proporzione rimane valida se si scambia ogni antecedente con il proprio conseguente.
a : b = c : d → b : c = d : c rimane invariata a · d = b · c
Proprietà del comporre
• In ogni proporzione la somma dei primi due termini sta al primo (o al secondo) termine, come la somma dei due restanti termini sta al terzo (o al quarto) termine. Ad es.
2 : 5 = 6 : 15
si ha (2+5) : 5=(6+15) : 15
ed anche (2+5) : 2=(6+15) : 6
Proprietà dello scomporre
• In ogni proporzione la differenza tra i primi due termini sta al primo (o al secondo) termine come la differenza tra i due restanti termini sta al terzo (o al quarto) termine.
3 :4 =9 : 12
si ha (4-3) : 4=(12-9) : 12
ed anche (4-3) : 3=(12-9) : 9
Come trovare il termine incognito in una proporzione
Se in una proporzione è incognito un termine medio, per trovare il suo valore è sufficiente dividere il prodotto dei due estremi per il medio noto; se invece è incognito un termine estremo, per trovare il suo valore è sufficiente dividere il prodotto dei due medi per l'estremo noto.
consideriamo la proporzione
3 : 6 = x : 8 come facciamo a trovare il termine incognito?
E' sufficiente applicare la proprietà fondamentale delle proporzioni
6·x = 3·8 → 6·x = 24 → x = 24/6 = 4
Questo procedimento è efficace anche se il termine incognito è uno dei due estremi
x : 25 = 3 : 15 applico la proprietà fondamentale delle proporzioni ottenendo
15·x = 3·25 → 15·x = 75 → x=75/15=5
:
=
:
 edutecnica
edutecnica