Operazioni con le frazioni

      

Con i numeri frazionari è possibile eseguire le due operazioni fondamentali dell’Aritmetica che sono l’addizione e la moltiplicazione assieme alle operazioni inverse alle due precedenti, cioè rispettivamente, la sottrazione e la divisione.
In questa pagina si considera anche il comportamento dei numeri frazionari rispetto all’operazione di elevamento a potenza assieme alle proprietà fondamentali delle operazioni aritmetiche e alle caratteristiche dell’insieme Q dei numeri razionali.

Ricordiamo la nomenclatura che riguarda i vari tipi di frazione

•   è frazione apparente se m è multiplo di n ; ad es.   è frazione apparente;

•  è frazione propria se m<n con ; ad es.   è frazione propria perchè

•   è frazione impropria se m>n con ; ad es. è frazione impropria perchè

• Si chiama reciproca della frazione  la frazione ad es. la reciproca di  è ; la reciproca di  non esiste.

• Ricordiamo poi che una frazione si dice irriducibile se m ed n sono primi tra loro :
per ridurre una frazione ai minimi termini basta dividere numeratore e denominatore per il loro M.C.D.

• Due frazioni  e si dicono frazioni equivalenti se e solo se  m·q=p·n  .

Addizione e sottrazione tra frazioni di ugual denominatore

      

Per addizionare due o più frazioni che hanno denominatore uguale, è sufficiente addizionare i numeratori e conservare il denominatore.

Esempi:

a)    

b)  

in generale:         

La sottrazione si esegue in base allo stesso principio.

Per sottrarre due frazioni che hanno denominatore uguale, è sufficiente sottrarre i numeratori e conservare il denominatore. Ad esempio:

a)   

b)   

c)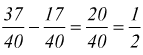   

In generale :   

Ricordiamo che quando appare una frazione, il denominatore della stessa deve sempre essere diverso da zero (0).

Addizione e sottrazione tra frazioni con diverso denominatore

      

Per addizionare e sottrarre frazioni con denominatore diverso, bisogna ridurle allo stesso denominatore riconducendosi così al caso visto prima.
Questa procedura è stata già applicata nel caso del confronto tra frazioni.
Per ridurre due o più frazioni allo stesso denominatore,è sufficiente sapere due cose:
a) il nuovo denominatore si può facilmente trovare calcolando il minimo comune multiplo (mcm) dei denominatori dati;
b) prima di cercare il nuovo denominatore bisogna ridurre tutte le frazioni assegnate ai minimi termini.

Per addizionare o sottrarre frazioni con diverso denominatore è sufficiente ridurle allo stesso denominatore e poi addizionare o sottrarre i numeratori ottenuti.

esempi:

a)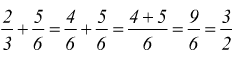    

b)          o anche    

c)       o anche   

Nel caso di somma e differenza tra frazioni si possono applicare le due formule rapide

    e    

anche se questa soluzione può portare a dei calcoli ulteriori più onerosi.

Il metodo più efficiente consiste nel calcolare mcm(n;q) minimo comune multiplo tra i due denominatori che diventerà il denominatore comune (denominatore della frazione risultante)

si divide il mcm trovato per ciascun denominatore

e si moltiplica il quoziente trovato per il rispettivo numeratore secondo la formula

lo stesso vale per la differenza:          ad es.

    mcm(3;5)=15         poi         lo stesso metodo può essere applicato per più frazioni.

Moltiplicazione tra frazioni

      

Per moltiplicare due frazioni è sufficiente moltiplicare tra loro sia i numeratori che i denominatori.

       per esempio    

questa regola può essere estesa al caso di tre o più frazioni

     per esempio      

ma potevamo ottenere lo stesso risultato semplificando prima     

Soltanto nella moltiplicazione di frazioni si può fare la semplificazione incrociata tra il numeratore di una frazione ed il denominatore di un'altra.

Per moltiplicare un numero naturale per una frazione, è sufficiente moltiplicare il numeratore per quel numero e conservare il denominatore. Ad es.

questa regola è derivata dalla precedente perchè se abbiamo un numero naturale che chiamiamo a da moltiplicare per una frazione b/c si può sempre scrivere

Divisione tra frazioni

      

Supponiamo di dover interpretare la scrittura

con dividendo 1 e divisore 2/3; cerchiamo il numero x che sia

La frazione inversa di una frazione assegnata è la frazione che si ottiene scambiando il numeratore con il denominatore.

Il quoziente tra l'unità (1) e una frazione è uguale all'inversa della frazione.

Ipotizziamo ora, di dover dividere       essendo 5/7 il dividendo e 2/3 il divisore, deve essere

   come nel caso precedente, moltiplichiamo il dividendo per l'inverso del divisore

   sostituendo questo valore alla x, si ottiene il risultato che volevamo      in generale è

Per dividere una frazione per un'altra è sufficiente moltiplicare la prima per l'inverso della seconda.

Questa regola può essere facilmente ricordata osservando che

Come si vede, ad un certo punto, moltiplichiamo l'espressione per la frazione `d/d` ma `d/d=1` che è neutro rispetto alla moltiplicazione: quindi non abbiamo fatto nulla; tuttavia questo artificio ci permette di effettuare una semplificazione che di fatto trasforma la divisione in moltiplicazione in modo conforme alla regola prima enunciata.

a)       oppure     

b)     oppure    

Una certa attenzione deve essere riservata alla forma

che deve essere risolta eseguendo le divisioni da sinistra verso destra; cioè si fa

si può procedere diversamente solo se vengono specificate delle parentesi come nel seguente caso

come si vede i risultati sono diversi

Potenza di una frazione

      

Se prendiamo ad esempio la frazione       è in generale

Per elevare una frazione ad un dato esponente, si elevano a quell'esponente il numeratore ed il denominatore.

Proprietà delle potenze

      

Nel caso delle frazioni rimangono valide anche le proprietà delle potenze

studiando le potenze, altre proprietà, verrebbero messe in evidenza, successivamente.

oltre alle regole più conosciute che rimangono:      e    

Proprietà commutativa

      

Con le frazioni (e dunque con i numeri razionali) rimangono valide tutte le proprietà definite per i numeri naturali:

    proprietà commutativa dell'addizione

In una addizione tra frazioni è possibile scambiare gli addendi

    proprietà commutativa della moltiplicazione

In una moltiplicazione tra frazioni è possibile scambiare i fattori

Proprietà associativa

      

    proprietà associativa dell'addizione

In una addizione tra frazioni è possibile sostituire a due (o più) di esse la loro somma.

     proprietà associativa della moltiplicazione

In una moltiplicazione tra frazioni è possibile sostituire a due (o più) di esse il loro prodotto.

Proprietà distributiva

      

Per moltiplicare la somma di due o più frazioni per un'altra frazione , si può moltiplicare per quest'ultima ciascun addendo e sommare i prodotti ottenuti.

La proprietà distributiva resta valida anche se all'interno delle parentesi al posto dell'addizione abbiamo una sottrazione.

queste proprietà rimangono anche se al posto della moltiplicazione abbiamo una divisione.

Numeri razionali

      

Nella teoria dei numeri, le frazioni, sono annoverate nella classe dei numeri razionali indicata con il simbolo Q i numeri razionali sono tutti i numeri frazionari dotati di segno (±) . In questo modo possiamo parlare di numeri del tipo

possono essere facilmente posizionati sulla retta numerica originata dall'insieme dei numeri interi relativi Z.

Nel seguente disegno si osserva come l'insieme dei numeri razionali incapsula l'insieme dei numeri interi relativi Z che a sua volta ingloba l'insieme dei numeri naturali N.

In sostanza per insieme dei numeri razionali, intendiamo dei numeri frazionari dotati di segno. E' molto semplice, produrre dei numeri razionali; basta dividere tra loro due interi relativi; ad es. come -3 e +4. A questo proposito, è necessario chiarire certe incertezze che si possono avere nella trattazione di un numero razionale relativo, quando il numeratore o il denominatore sono negativi; eseguendo la divisione di -3 per +4

     dovremmo scrivere      perchè    

alla stessa conclusione si arriva anche se solo il denominatore fosse negativo. La rappresentazione del numero è corretta; perchè un numero negativo diviso per un numero positivo, produce comunque un numero (3/4) che è complessivamente negativo. Inoltre la stessa operazione è formalmente reversibile (eseguibile al contrario). La maggior parte degli errori che si compiono durante lo svolgimento delle espressioni aritmetiche sono attribuibili a questi dettagli.

Riassumendo le caratteristiche dei numeri razionali, potremmo dire:
• L'insieme Q dei numeri razionali è illimitato sia superiormente che inferiormente; non esistono quindi un numero razionale più grande o più piccolo.

• Nell'insieme Q dei razionali hanno sempre senso le due operazioni fondamentali dell'aritmetica : addizione e moltiplicazione e le loro operazioni inverse di sottrazione e divisione (escludendo la divisione per 0). Si dice pertanto, che l'insieme Q dei numeri razionali è chiuso rispetto alle operazioni aritmetiche.

• Le due operazioni fondamentali di addizione e moltiplicazione, godono della proprietà commutativa ed associativa.

• Entrambe le operazioni dirette di addizione e moltiplicazione possiedono l'elemento neutro.

L'elemento neutro dell'addizione è 0 perchè

      (per ogni valore di a/b appartenente a Q)

L'elemento neutro della moltiplicazione è 1 perchè

• Dato un qualunque numero razionale esiste il suo opposto ad es.

• Dato un qualunque numero razionale diverso da zero esiste il suo inverso (o reciproco) ad es.

• L'addizione e la moltiplicazione sono legate tra loro dalla proprietà distributiva.

• L'insieme Q è ordinato, nel senso che dati due numeri razionali tra loro diversi, è è possibile stabilire quale dei due è minore dell'altro.

• L'insieme Q è denso, infatti, assegnati due numeri razionali tra loro diversi, esiste sempre un altro numero razionale compreso tra i primi due.