Frazioni

      

La classe dei numeri naturali N={0; 1; 2; 3:..} molto facile da rappresentare graficamente; basta prendere un quaderno a quadretti e tracciare una semiretta su cui segnare delle tacche equidistanti tra loro a partire dall’origine 0 (zero).

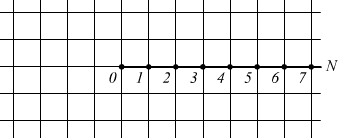
La semiretta dei numeri naturali è illimitata verso destra, visto che ogni numero ha un suo successore più grande di una unità (rispetto al precedente).
Invece, una limitazione per i numeri naturali è proprio lo zero, perchè impedisce formalmente delle sottrazioni quando il sottraendo è maggiore del minuendo

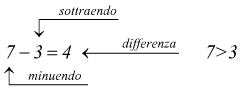
In questo caso il sottraendo è maggiore del minuendo (7>3); il risultato (4) è ancora un numero appartenente all'insieme dei numeri naturali N anche perché è chiaramente identificabile sulla semiretta di N.
Ma quest'altro caso?

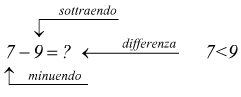
E' stato così necessario ampliare la classe dei numeri naturali, allungando la semiretta N, introducendo l'insieme dei numeri interi relativi
Z={-2; -1; 0; 1; 2; 3:..}

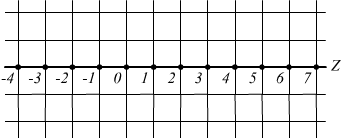
Con gli interi relativi e quindi con l'introduzione dei numeri negativi, una sottrazione come la precedente può avere una sua congrua rappresentazione anche nel caso in cui il sottraendo sia maggiore del minuendo.

        

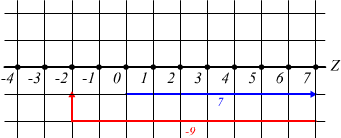
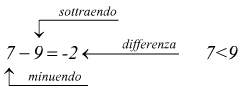
abbiamo a che fare con dei numeri relativi; sono numeri relativi quei numeri il cui valore dipende dal segno che li precede cioè il loro valore è relativo al segno.

Mentre la moltiplicazione, essendo in pratica una somma ripetuta, non pone problemi all'interno di N e di Z, la divisione, viene definita ed assume significato solo come operazione inversa della moltiplicazione.

Ad es. possiamo chiederci se abbia senso una uguaglianza come la seguente
7·x=21
cioè, esiste un numero che moltiplicato per 7 fornisce come risultato 21?
Certo che esiste: si tratta del 3 e quindi scriveremo 7·3=21 e per indicare la divisione effettuata scriviamo 21/7=3 oppure (indifferentemente) 21:7=3.

Non sempre, volendo restare all'interno dell'insieme dei numeri naturali N, la divisione è possibile; ad es. nella seguente uguaglianza x·4=15 non è possibile individuare il numero naturale x che moltiplicato per 4 restituisca 15.

Sarà necessario introdurre una nuova classe di numeri: i numeri razionali che consentono di eseguire in ogni caso l'operazione di divisione attraverso la loro espressione più comune che è la frazione.
Alcune frasi che diciamo usualmente posso essere sinteticamente rappresentate in forma matematica.

Si chiama unità frazionaria la scrittura

Basandosi poi su unità frazionarie, si può costruire qualsiasi frazione: ad esempio

Noi, chiamiamo frazione una scrittura del tipo

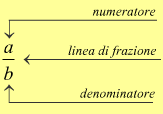
dove a e b sono numeri naturali e b≠0
a si chiama numeratore
b si chiama denominatore
• Il denominatore (de)nomina le parti, cioè dice in quante parti uguali è stata suddivisa la grandezza.
• Il numeratore, invece, numera le parti, cioè dice quante di queste parti sono state prese in considerazione.

Frazioni proprie improprie ed apparenti

      

• una frazione in cui il numeratore è minore del denominatore è una frazione propria.

• una frazione in cui il numeratore è maggiore o uguale al denominatore è una frazione impropria.

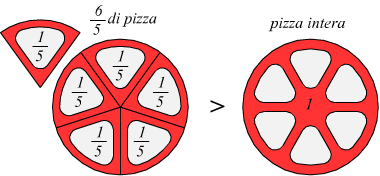
• una frazione in cui il numeratore è un multiplo del denominatore è una frazione apparente.

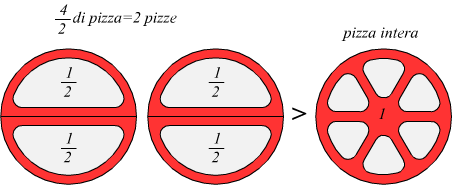
Le frazioni apparenti coincidono sempre con i numeri naturali.

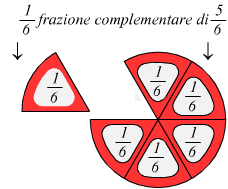
Se abbiamo una frazione propria, la sua frazione complementare quella frazione che indica la parte mancante per arrivare all'intero.

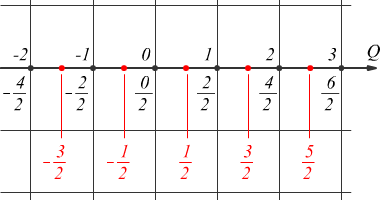
All'insieme dei numeri naturali e degli interi relativi può essere ora aggiunto l'insieme dei numeri razionali che può essere anch'esso rappresentato sulla retta numerica. Utilizzando come unità frazionaria 1/2

poi con frazione unitaria 1/3

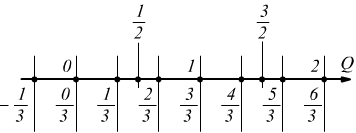
poi con frazione unitaria 1/4

Come si può immaginare continuando a suddividere la retta con unità frazionarie sempre più piccole, la densità dei punti che rappresentano le frazioni andrà ad aumentare. Inoltre si può osservare che

• una frazione rappresenta 1, solo se numeratore e denominatore sono uguali;
• una frazione rappresenta lo 0 solo se il numeratore è uguale a 0.
• una frazione rappresenta un numero intero solo se il numeratore è un multiplo del denominatore
• ad uno stesso punto sulla retta possono corrispondere più frazioni
ad es. 3/2 e 6/4 si vede nel disegno che coincidono e poi si ha semplificando

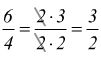    queste frazioni sono equivalenti

Sono chiamate equivalenti, le frazioni a cui corrisponde uno stesso punto sulla retta numerica.
un'altra sequenza di frazioni equivalenti è

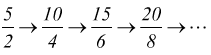
si nota che per passare da una frazione all'altra, basta moltiplicare numeratore e denominatore per lo stesso numero.

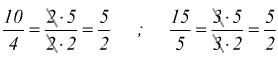
Una frazione si trasforma in una equivalente quando numeratore e denominatore vengono moltiplicati per lo stesso numero naturale (diverso da 0).

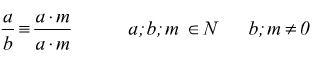
Il segno ≡ nella scrittura precedente è il simbolo di equivalenza ed in questo caso sta a significare che alle due frazioni (che sembrano formalmente diverse) corrisponde lo stesso punto sulla semiretta numerica; o alternativamente, sono due modi diversi per indicare lo stesso numero razionale.
Le frazioni equivalenti hanno lo stesso valore.

Semplificazione di una frazione

      

Il ragionamento precedente è vero anche al contrario.

Una frazione si trasforma in una equivalente quando numeratore e denominatore vengono divisi per lo stesso numero naturale
(diverso da 0).

Queste osservazioni danno luogo ad una delle più importanti regole della divisione e della matematica : la proprietà invariantiva della divisione:

  Proprietà invariantiva della divisione   
Il valore di una frazione non cambia se numeratore e denominatore vengono contemporaneamente divisi o moltiplicati per uno stesso numero diverso da zero

Dunque, formalmente 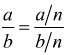        ad es.

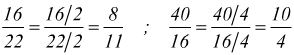
Una frazione si dice ridotta ai minimi termini quando numeratore e denominatore sono primi tra loro. Ad es.

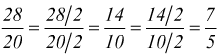  ma si poteva anche eseguire la riduzione ai minimi termini

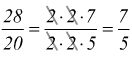   e semplificare

	: numeratore
	: denominatore

La riduzione di una frazione ai minimi termini si può eseguire mediante semplificazioni successive, fino a che numeratore e denominatore risultano primi tra loro; oppure si può calcolare il M.C.D. tra numeratore e denominatore e dividere entrambi i termini per l'MC.D. trovato.

Un numero razionale può essere indicato da tante frazioni tra loro equivalenti quante si vuole. Al contrario, ogni frazione rappresenta un ben determinato numero razionale.

Gli antichi greci, pensavano che esistessero solo numeri interi e che tutti gli altri numeri possibili potessero essere scritti in forma di frazione, di rapporti tra interi, come 22/7; ma poi i pitagorici, attorno al 600 a.C. scoprirono che esistevano dei numeri come

che non potevano essere espressi come rapporto tra numeri interi; questi numeri vennero chiamati irrazionali. La loro introduzione costituisce un ulteriore ampliamento delle precedenti classi dei numeri interi e razionali.

Confronto tra frazioni

      

A parità di numeratore, è più grande la frazione che ha il denominatore più piccolo.

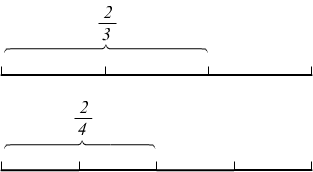
A parità di denominatore è più grande la frazione che ha numeratore maggiore.

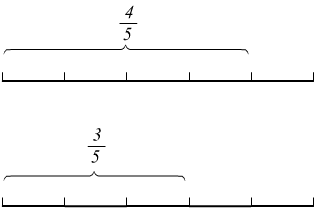
Questa seconda modalità, è certamente più intuitiva.
Se pensiamo che se abbiamo una frazione ne esistono infinite altre ad essa equivalenti ; se dobbiamo confrontare tra loro due frazioni, sarà opportuno ricondurle allo stesso denominatore per poi confrontare i numeratori.
Conviene per facilitare il calcolo che il denominatore coincida con l'mcm dei denominatori.

Numeri razionali

      

Nell'insieme dei numeri naturali non sempre, dati due numeri, è possibile trovarne un altro compreso tra questi due assegnati.
Ad esempio tra il 2 ed il 5 ci sono altri due numeri; mentre tra 8 e 9 non ce ne sono.

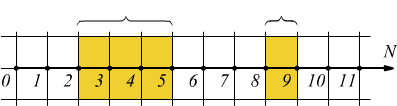
E' impossibile trovare un numero naturale tra altri due numeri naturali consecutivi.

Nel caso dei numeri razionali, le cose sono un po' diverse. Consideriamo due frazioni (due numeri razionali)

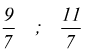
solo il numero razionale      è compreso tra questi due numeri; consideriamo ora due frazioni equivalenti alle due precedenti:

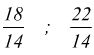      tra queste due sono compresi i numeri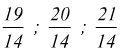    

se poi consideriamo altre due frazioni equivalenti a quelle inizialmente assegnate

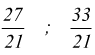   tra queste due sono compresi i numeri       

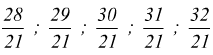
i numeri razionali compresi, sono ancora di più; eppure sulla retta numerica due frazioni equivalenti coincidono con lo stesso punto.
Inoltre si nota che più aumenta il denominatore della frazione equivalente, più aumentano i punti compresi tra i due numeri razionali inizialmente assegnati.

I matematici descrivono questa proprietà dicendo che l'insieme dei numeri razionali è denso.

Si conclude che: tra due numeri razionali qualsiasi ne esistono infiniti altri compresi tra questi due.
Ma si può esprimere la stessa cosa dicendo che nell'insieme dei numeri razionali, a differenza di quello che accade per i numeri naturali; dato un numero qualsiasi non esiste un suo successivo.

Dimostrazione dell'irrazionalità di √2

      

Se si assume che $√2$ sia un numero razionale che possa essere descritto dal rapporto $$A/B$$ dove A e B sono due numeri interi, si arriverebbe ad una contraddizione che dimostrerebbe che questa nostra asserzione è falsa.

Se sia A che B sono numeri pari, possiamo cancellare il fattore comune 2, ripetendo se necessario l'operazione, finché almeno uno dei due interi non sarà dispari; ciò significa che se possiamo scrivere

$$√2=A/B\;→$$fattorizzando per 2 fin quando possibile$$\;→√2=M/N$$

dove M e N sono due interi e almeno uno dei due è dispari (magari lo sono entrambi). Eleviamo al quadrato quest'ultima equazione e moltiplichiamo entrambi i membri per N², così, otteniamo
2N²=M²
essendo uguale ad un multiplo del 2, M² è pari.
Questo significa che M è pari, perchè il quadrato di un numero dispari è sempre dispari.
Si può mostrare che anche N è pari.

Dato che M è pari, si può scrivere M=2K dove K è un altro intero; di conseguenza M²=4K². e quindi andremo a sostituire nell'eq. precedente
2N²=4K² → N²=2K²
questo significa che N² essendo uguale ad un multiplo del due è pari e di conseguenza è pari anche N.
Abbiamo già contraddetto quello che dicevamo all'inizio; che almeno uno dei due numeri M o N doveva essere dispari.
L'unica possibile causa (noi abbiamo solo seguito le regole della matematica) è che la nostra ipotesi di partenza

$$√2=A/B\;\;\;$$ sia falsa

Abbiamo dimostrato che $√2$ non è un numero razionale, bensì irrazionale.

La sua rappresentazione decimale non risulta finita (con un numero limitato di cifre dopo la virgola) ne illimitata periodica, come può accadere nel caso dei numeri razionali.
La sua rappresentazione decimale risulta illimitata e non periodica.