Integrale indefinito
Si considera una funzione f(x), definita nell'intervallo [a,b]; se per questa funzione ne esiste un'altra F(x) tale che:
![]()
F(x) viene chiamata funzione primitiva di f(x).
Se due funzioni F(x) e G(x) hanno in [a,b] la stessa derivata, la loro differenza è costante. Infatti.
![]()
ne consegue che
![]() costante
quindi
costante
quindi
![]()
Se una f(x) possiede in [a,b] una primitiva F(x) , ogni altra funzione ottenuta aggiungendo ad F(x) una costante arbitraria c, è anch'essa primitiva di f(x).
All'insieme di tutte le infinite primitive di f(x) si da il nome di integrale indefinito di f(x) indicandolo col simbolo:
![]()
Questo insieme è pienamente determinato quando è nota anche una sua sola primitiva
![]() con,
ovviamente F'(x)=f(x).
con,
ovviamente F'(x)=f(x).
Come si intuisce l'integrazione è l'operazione inversa della derivazione.
Ricordando la formula per la derivazione di una funzione composta:
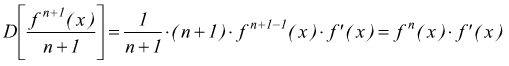
si deduce 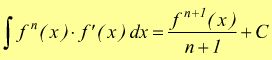
oppure 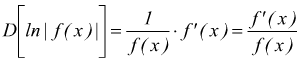 da
cui si ottiene
da
cui si ottiene
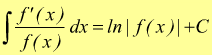
altri integrali indefiniti riconducibili ad integrali immediati sono riportati in in questa pagina .
Integrazione per sostituzione
Se nell'integrale indefinito:
![]() si
pone
si
pone ![]()
differenziando si ottiene:
![]() sostituendo
sostituendo ![]()
Accade a volte che la determinazione di quest'ultimo integrale sia più facile di quello precedente. Esempi:
I ) 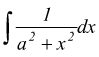 ponendo
ponendo
![]()
sostituendo
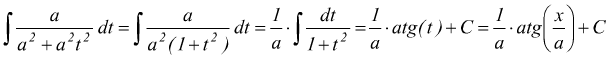
II ) ![]() ponendo
ponendo
![]()
si avrebbe ![]() e differenziando
e differenziando  quindi
quindi
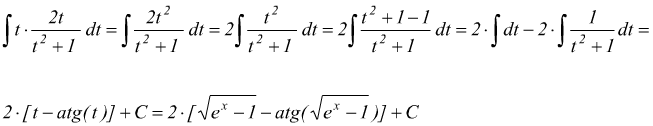
III ) ![]() ponendo
ponendo
![]()
![]()
essendo 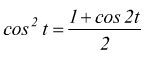 si
ha
si
ha

avendo posto 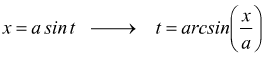 e
inoltre
e
inoltre
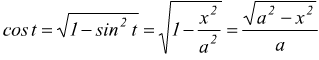 in
definitiva
in
definitiva
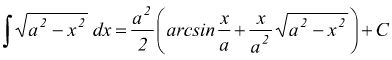
IV ) 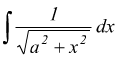
![]()
si ha  differenziando
differenziando
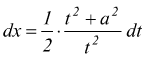 sostituendo
sostituendo
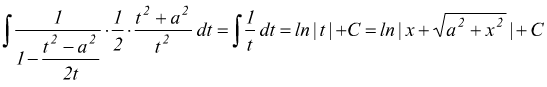
Integrazione per parti
Dalla regola della derivazione del prodotto
![]()
si ricava
![]()
integrando entrambi i membri
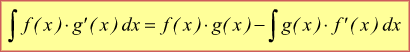 essendo
essendo

si può riscrivere
![]()
dg(x) si chiama fattore
differenziale
f(x) si chiama fattore
finito
La regola dell'integrazione per parti, può allora essere enunciata nel modo seguente:
L'integrale del prodotto di due funzioni , di cui una sia presa come fattore finito, è uguale al prodotto del fattore finito per l'integrale del fattore differenziale, diminuito dell'integrale del prodotto della derivata del fattore finito per l'integrale del fattore differenziale. Esempi:
I ) ![]() se
poniamo lnx come fattore finito e dx come fattore differenziale
se
poniamo lnx come fattore finito e dx come fattore differenziale
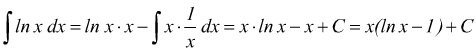
II ) ![]() se
poniamo atgx come fattore finito e dx come fattore differenziale
se
poniamo atgx come fattore finito e dx come fattore differenziale

III ) ![]() se
poniamo x come fattore finito e exdx come fattore
differenziale
se
poniamo x come fattore finito e exdx come fattore
differenziale
![]()
IV ) ![]() se
poniamo x2 come fattore finito e exdx
come fattore differenziale
se
poniamo x2 come fattore finito e exdx
come fattore differenziale
![]() per
l'esempio precedente
per
l'esempio precedente
![]()
V ) ![]() se
poniamo x come fattore finito e cosx dx come fattore differenziale
se
poniamo x come fattore finito e cosx dx come fattore differenziale
![]()
Integrazione di funzioni razionali
Una funzione razionale è il rapporto ![]() di
due polinomi f(x) e g(x).
di
due polinomi f(x) e g(x).
Se il grado della f(x) non è minore del grado della g(x), eseguendo la divisione:
![]()
essendo P(x) il quoziente ed r(x) il resto di grado inferiore
a g(x).
Dividendo per g(x) si ottiene:
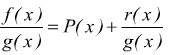
una funzione razionale è la somma di un polinomio e di una funzione razionale fratta il cui numeratore è un polinomio di grado inferiore al grado del polinomio denominatore.
Si dimostra che questa funzione si può scomporre nella somma di funzioni razionali elementari del tipo
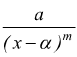
con le quantità a ed sono costanti reali o complesse e gli esponenti m sono numeri interi. Possono esserci i seguenti casi:
I ) Si sanno determinare tutte le radici reali del polinomio denominatore
ed esse sono radici semplici.
Cioè se n è il grado di g(x), si ha:
![]() con
con
![]()
In questo caso si possono determinare n costanti reali A1,A2,…,An tali che:
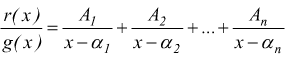 quindi
quindi
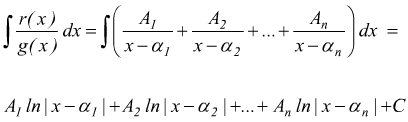
Ad esempio
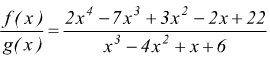 eseguendo
la divisione
eseguendo
la divisione
![]()
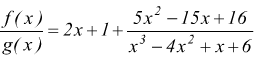
polinomio ![]() si
annulla per
si
annulla per ![]() per
cui
per
cui
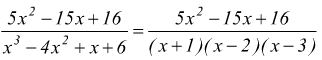
basta determinare le tre costanti A, B, C tali che:
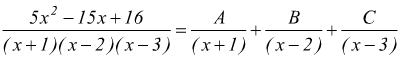
Riconducendo a forma intera
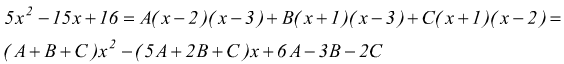
dovrà essere
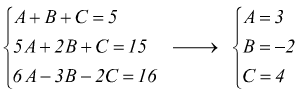 in
definitiva
in
definitiva
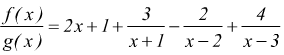 quindi
quindi
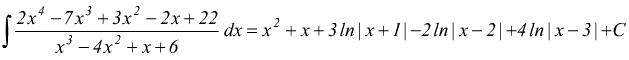
II ) Può accadere che una delle radici del denominatore abbia molteplicità maggiore di 1.
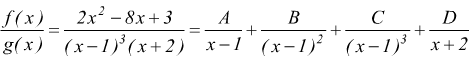 cioè
cioè
![]()
ne segue ![]()
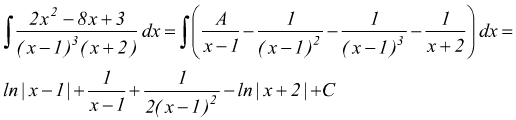
III ) Da ultimo facciamo l'ipotesi in cui al denominatore vi sia un trinomio di secondo grado col Δ<0 e quindi avente radici complesse.
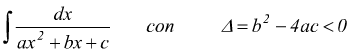
essendo 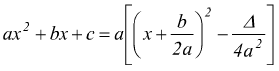 poniamo
poniamo
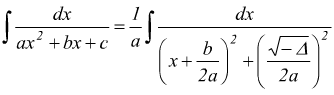 integriamo
per sostituzione
integriamo
per sostituzione
ponendo  differenziando
differenziando 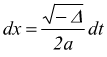 sostituendo
sostituendo
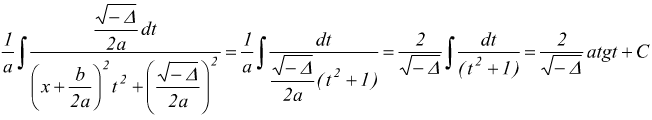
quindi
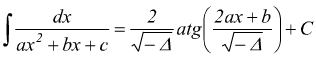
Integrale definito
Se F(x) è una primitiva di f(x):
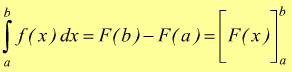
L'integrale definito di una funzione esteso all'intervallo [a,b] è dato dalla differenza tra i valori che una sua primitiva assume per x=b e x=a. Ad esempio
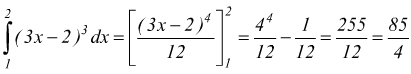
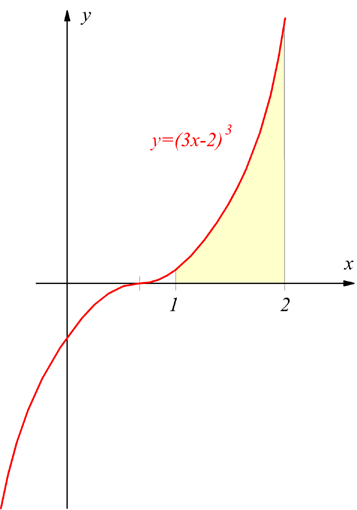
E' utile ricordare che l'integrale di una funzione y=f(x)
esteso all'intervallo [a,b] rappresenta l'area sottesa (con segno)
fra la linea di funzione y=f(x) e l'asse delle ascisse.
Nel nostro caso,integrando la funzione
y=(3x-2)3 nell'intervallo[2,1]
.
Il valore dell'integrale ottenuto, coincide con l'area evidenziata
in giallo.
 edutecnica
edutecnica