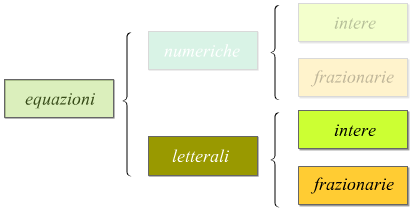
Equazioni numeriche frazionarie

Rispetto alle equazioni numeriche intere questo tipo di equazione può avere dei termini che hanno al denominatore l'incognita x.
Per esse, bisogna sempre verificare le condizioni di esistenza (C.E.) e ricavare il dominio di esistenza .

Il dominio di un’equazione è l’insieme dei numeri reali che sostituiti al posto dell'incognita trasformano l’equazione in una uguaglianza dotata di significato, e che dunque, può essere vera o falsa.

Le soluzioni di un’equazione devono appartenere al suo dominio.
Se non si dice nulla è sottinteso che il dominio di un’equazione è l’insieme R dei numeri reali.

Le equazioni intere ad una incognita hanno tutte come dominio l’insieme R dei numeri reali.

Nel caso delle equazioni frazionarie il dominio è costituito da R con l'esclusione di valori che annullano i denominatori.

Le condizioni di esistenza impongono che i denominatori presenti nell’equazione non debbano annullarsi.
Ad es. per

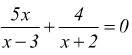deve essere

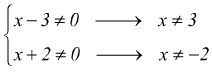
i valori di x=3 e di x=-2 annullano i denominatori rendendo l'equazione priva di significato: questi numeri devono essere esclusi dal dominio di esistenza quindi le condizioni di esistenza (o di accettabilità) sono:

C.E. x≠3 ∧ x≠-2 mentre il dominio di esistenza si scrive D≡R-{3;-2}

Quando siamo in presenza di un'equazione frazionaria bisogna sempre far attenzione ai denominatori.

Una volta individuate le condizioni di esistenza (C.E.) partendo dal presupposto che i denominatori non siano nulli si può cercare di ricondurre l'equazione alla forma `ax=b` per risolverla con lo stesso schema delle equazioni numeriche intere:

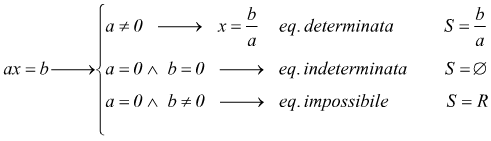
Soluzione di un'equazione frazionaria

Per risolvere le equazioni frazionarie si procede allo stesso modo visto per le equazioni intere, ma si deve tener conto di una condizione ulteriormente restrittiva: le eventuali soluzioni che non soddisfano le condizioni di esistenza (C.E.) devono essere scartate.
Nelle equazioni fratte almeno un denominatore è un polinomio nella variabile incognita x.
Visto che il denominatore di una frazione non può mai essere zero e che i denominatori di un'equazione fratta dipendono dalla x, vanno esclusi tutti i valori di x che annullano i polinomi nei vari denominatori.

E' infatti, possibile dimostrare il seguente criterio:

Moltiplicando o dividendo entrambi i membri di un'equazione per la stessa espressione contenente l'incognita x che, per qualsiasi valore di x soddisfi le condizioni di esistenza (C.E.), si ottiene un'equazione equivalente a quella iniziale le cui soluzioni soddisfano le C.E. iniziali.

Con questo presupposto possiamo definire il procedimento per la risoluzione di un'equazione frazionaria:

• Se è possibile si scompongono in fattori i denominatori dell'equazione .
• Si valutano le condizioni di esistenza e si trova il dominio dell'equazione.
• Si riducono entrambi i membri allo stesso denominatore.
• Si eliminano i denominatori moltiplicando entrambi i membri per il denominatore comune.
• Si risolve l'equazione intera così ottenuta.
• Si confrontano le soluzioni trovate con le condizioni di esistenza e si scartano le eventuali soluzioni che non soddisfano tali condizioni.

Ad esempio, risolviamo l'equazione

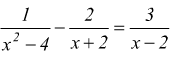scompongo i denominatori dove possibile

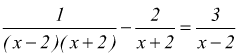
poniamo le condizioni di esistenza C.E. x≠2 ∧ x≠-2
il mcm dei denominatori è `(x-2)(x+2)`

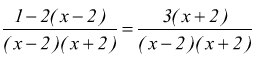
eliminiamo i denominatori moltiplicando entrambi i membri per il denominatore comune
(possiamo farlo perchè abbiamo fatto l'ipotesi x≠2 ∧ x≠-2).

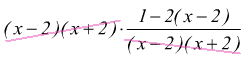
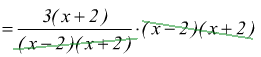
ricaviamo

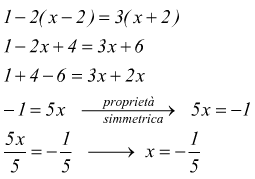
La soluzione trovata `x=-1/5` soddisfa le condizioni di esistenza, quindi è accettabile.

Per quanto visto, il procedimento non è molto differente dalla soluzione di un'equazione numerica intera; ma bisogna sempre controllare che il risultato non interferisca con le condizioni di esistenza, come si vede dal seguente esempio.

scomponiamo i denominatori

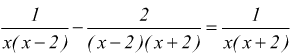
troviamo le condizioni di esistenza C.E. x≠0 ∧ x≠2 ∧ x≠-2
il denominatore comune è `x(x-2)(x+2)`; facciamo il denominatore comune

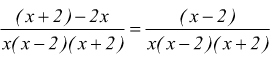
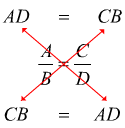
possiamo notare che a questo punto del procedimento, l'equazione si trova sempre nella forma `A/B=C/D`
quindi possiamo anche fare il prodotto in croce.

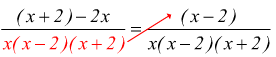
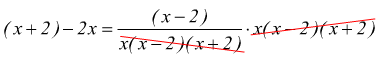
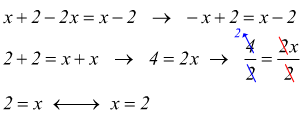
la soluzione trovata : x=2 rappresenta una violazione di una delle condizioni di esistenza precedentemente ricavate quindi l'equazione assegnata è impossibile; l'insieme delle sue soluzioni è vuoto S=∅.

Equazioni letterali

Un'equazione letterale è un'equazione in cui, oltre all'incognita compaiono altre lettere (chiamate parametri).
Praticamente tutte le formule fisiche sono equazioni letterali, si tratta, dunque, di un modello algebrico particolarmente importante proprio perchè permette di rappresentare moltissimi problemi reali.
Questa maggior generalità implica però che il numero di soluzioni e la loro esistenza dipende dai valori assunti dai parametri.

Equazioni letterali intere

Dato che i parametri che compaiono in un'equazione letterale rappresentano dei numeri, la risoluzione di un'equazione letterale intera non differisce sostanzialmente da un'equazione numerica intera.
Restano quindi validi i primi due principi di equivalenza; in particolare il secondo: moltiplicando o dividendo entrambi i membri di un'equazione per uno stesso numero diverso da zero si ottiene un'equazione equivalente a quella data.
Perciò tutte le volte che occorre moltiplicare o dividere entrambi i membri di un'equazione per una stessa espressione letterale è necessario tener presente che tale espressione potrebbe annullarsi in corrispondenza di alcuni valori dei parametri.

Le equazioni letterali intere ad una incognita sono equazioni in cui oltre all'incognita x, compaiono uno o più parametri, cioè lettere che rappresentano numeri noti anche se non specificati; come ad esempio.

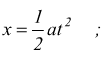
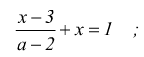
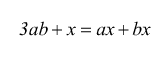
pur potendo esserci delle frazioni, l'incognita x NON appare mai al denominatore.

Soluzione di un'equazione letterale intera

Anche per questo tipo di equazione la strategia risolutiva consiste nel semplificare progressivamente l'equazione iniziale, attraverso una serie di equazioni equivalenti, fino a ricondurre l'equazione data alla forma

con A e B che possono essere numeri, monomi o polinomi contenenti esclusivamente parametri .

• Se A è un numero diverso da zero la soluzione è `x=B/A` .

• Se A=0 l'equazione diventa `0*x=B` quindi è indeterminata in corrispondenza dei valori degli eventuali parametri per cui `B=0` ed è impossibile per i valori per cui `B!=0`.

• Se A è un'espressione letterale , si cercano gli eventuali valori dei parametri per cui `A=0`. Se tali valori non esistono l'equazione è determinata e la sua soluzione è `x=B/A` altrimenti si devono determinare per quali valori dei parametri il valore di A si annulla e si fanno delle valutazioni che consistono nel determinare i valori delle lettere per i quali l'equazione `Ax=B` è determinata,indeterminata o impossibile. ad esempio

applicando il secondo principio otterremo immediatamente

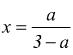ma deve essere rispettata la condizione `a!=0` si conclude che

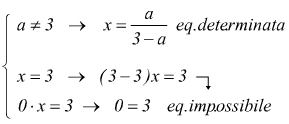
sono previste diverse soluzioni a secondo del valore assunto dal parametro ad esempio

può essere riscritta come

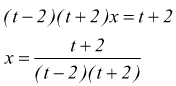
Equazioni letterali frazionarie

Nel caso delle equazioni letterarie frazionali l'incognita deve apparire al denominatore di qualche frazione. alcuni esempi di equazioni frazionarie sono:

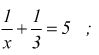
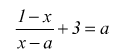
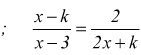
In linea generale, per risolvere un'equazione letterale frazionaria basta seguire gli stessi procedimenti effettuati per le equazioni intere numeriche e frazionarie, visto che i parametri possono essere considerati dei valori costanti.
Si impone una certa cautela nella valutazione del risultato che come detto non può interferire con le condizioni di esistenza dell'equazione assegnata. Ad esempio

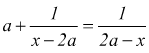con `C.E. x!=0`

moltiplico i membri per `2a-x`

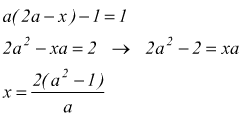
dove deve essere `x!=a`

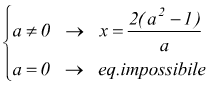
infatti nel secondo caso l'equazione diventa

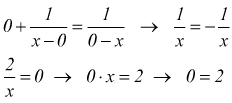
che è impossibile.