Multipli
Assegnato un numero naturale n appartenente all’insieme dei numeri naturali n∈N=1,2,3,... chiamiamo multiplo di n, il prodotto tra n ed un altro qualsiasi numero naturale.
• I multipli di un numero diverso da 0 sono infiniti.
• Ogni numero naturale maggiore di 1 è multiplo almeno di due numeri:
uno di essi è uguale al numero dato, l'altro è 1. Ad es. 5×1=5.
• E' possibile considerare 0 come multiplo di qualsiasi altro numero (dato
che n×0=0) .
• I multipli del 2 sono i numeri pari, tuuti gli altri sono i numeri dispari.
Divisori
Un numero naturale d è un divisore di
un numero naturale n se n è un multiplo di d. ad es. se n=12 i numeri
1,2,3,4,6,12 sono divisori di 12.
• I divisori di un numero n diverso da 0 sono in numero finito.
• Ogni numero naturale diverso da 0 è divisore di infiniti numeri (tutti
i suoi multipli).
• Il numero 0 non è divisore di alcun numero tranne che di se stesso.
Questo perché se n≠0 non esiste nessun numero d per cui si possa scrivere
0×d=n .
• i numeri pari hanno come divisore 2 i numeri dispari no.
Due importanti regole valide nella divisione tra numeri naturali sono le seguenti :
Supponiamo di avere due numeri naturali: n ed m allora
(I) Se entrambi i numeri n ed m sono divisibili per un terzo numero d, saranno divisibil per d anche n+m ed n-m.
(II) Se un numero d è divisore di un numero m che a sua volta è divisore di un numero n allora si può dire che d è divisore anche di n.
Criteri di divisibilità
Un criterio di divisibilità, è un modo per riconoscere partendo dalla scrittura di un numero e senza eseguire divisioni, se un numero è divisibile per un altro.
• Se è possibile scrivere un numero come somma di diversi addendi tutti divisibili per uno stesso divisore d, allora anche il numero inizialmente assegnato è divisibile per d.
• un numero è divisibile per 2 quando
l'ultima cifra a destra è pari. Ad es.
96 l'ultima cifra a
destra è pari, dunque 96 è divisibile per 2
333 l'ultima cifra a destra
non è pari, dunque 333 non è divisibile per 2
• un numero è divisibile per 5 quando
l'ultima cifra a destra è 0 o 5. Ad es.
695 l'ultima cifra adestra è 5,
dunque 695 è divisibile per 5
220 l'ultima cifra a destra è 0, dunque
220 è divisibile per 5
• un numero è divisibile per 10
quando l'ultima cifra a destra è 0. Ad es.
3460 l'ultima cifra a destra è 0,
dunque 3460 è divisibile per 10
• un numero è divisibile per 4 quando
è divisibile per 4 il numero formato dalle sue ultime due cifre a destra.
Ad es.
1732 le ultime
due cifre a destra sono 32 (divisibile per 4)
18142 le ultime due cifre a destra
sono 42 (divisibile per 4)
• Un numero è divisibile per 25
quando è divisibile per 25 il numero formato dalle sue due ultime cifre
a destra (che possono essere, dunque, solo 00 25 50 75). Ad es.
14740 il numero che costituisce le due
ultime cifre a destra non è divisibile per 25, quindi, 14740 non è divisibile
per 25.
2650 il numero che costituisce
le due ultime cifre a destra è divisibile per 25, dunque, 2650 è divisibile
per 25 .
• un numero è divisibile per 3 o
è divisibile per 9 quando la somma
delle sue cifre è un numero divisibile per 3 o per 9. Ad es.
2724 → 2+7+2+4=15 divisibile per
3
749 → 7+4+9=20 non è divisibile per
3
1809 → 1+8+0+9=18 divisibile per
9 (ed anche per 3)
Numeri primi
Ogni numero naturale che ammetta soltanto due divisori, se stesso e l'unità, si chiama numero primo.
Sono ad es. numeri primi: 2, 3, 5, 7, 11,..17..
• Il numero 1 che ammette un solo divisore non è considerato un numero
primo.
• Il numero 0 che ammette infiniti divisori, non è un numero primo.
• Il più piccolo numero primo è il 2 che è anche l'unico numero primo
pari.
• Il numero dei numeri primi è infinito.
Come si può immaginare l'unico criterio per stabilire se un numero è primo,
consiste nell'andare per tentativi.
Si divide il numero assegnato per i successivi
numeri primi 2, 3, 5, 7... se si arriva a trovare un quoziente esatto (senza
la virgola) il numero non è primo; altrimenti si continuano le divisioni
fino a quando si trova un quoziente minore od uguale al divisore. Se anche
questo quoziente non è esatto, si può affermare che il numero assegnato
è primo.
Numeri composti
I numeri naturali maggiori di 2 che non sono
primi si chiamano numeri composti.
I numeri composti sono quelli che si possono scrivere come il prodotto di
due fattori maggiori di 1.
Da questa definizione si deduce che l'insieme dei numeri naturali può essere scomposto in tre sottoinsiemi:
• l'insieme contenente 0 ed 1 ( che come detto non sono numeri primi);
• l'insieme dei numeri primi;
• l'insieme dei numeri composti;

Esempi di numeri composti sono
4=2×2
8=2×4
12=3×4
15=3×5
talvolta è possibile scomporre ulteriormente i fattori di un numero composto; ad es. 12=3×2×2
Quando tutti i fattori sono diventati numeri primi e non è più possibile nessuna ulteriore scomposizione si dice che il numero è stato scomposto in fattori primi.
Scomposizione in fattori primi
E' possibile dimostrare che :
assegnato un qualsiasi numero naturale composto,
esiste una ed una sola scomposizione in fattori primi che lo rappresenta.
anche se le strade per arrivare a questa (unica) rappresentazione possono
essere più di una.
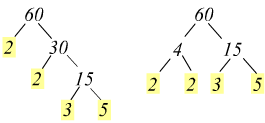
cioè 60=2×2×3×5.
Per eseguire la scomposizione in fattori primi di un numero conviene cominciare
ad eseguire la divisione del numero assegnato per 2 (se è possibile) e poi
dividere il quoziente ottenuto ancora per 2 e così via, fino a raggiungere
un quoziente non divisibile per 2.
A partire da questo quoziente (che potrebbe anche essere il numero di partenza
se questo è dispari) si passa a dividere per 3; cioè per il numero primo
immediatamente più grande di 2; successivamente si passa a 5 e a 7 e così
ricordandosi sempre che bisogna dividere per numeri primi progressivamente
crescenti.
Massimo Comune Divisore M.C.D.
Dati due numeri viene chiamato Massimo Comune Divisore il più grande tra i loro divisori comuni.
I numeri 12 e 18 hanno in comune quattro divisori : 1, 2, 3, 6 il pù grande
tra di loro è il Massimo Comune Divisore e così si può scrivere
MCD(12;18)=6
Il Massimo Comune Divisore di due o più numeri che non hanno alcun divisore
in comune al di fuori dell'unità, è 1 stesso. Ad es.
MCD(17;36;57)=1
in questo caso i numeri si dicono primi tra di loro.
Due o più numeri composti (che non sono per definizione numeri primi) possono
essere primi tra di loro come ad esempio
MCD(8;9)=1.
Se uno dei numeri assegnati è divisore degli altri, questo è il Massimo
Comune Divisore. ad es.
MCD(15,30,75)=15
Per i numeri piccoli l'MCD si può trovare anche senza particolari calcoli.
Per i numeri un po' più elevati è necessario ricorrere alla scomposizione
in fattori primi secondo la seguente procedura:
(I) scomporre i numeri in fattori primi evidenziando le potenze
(II) cercare i fattori primi che appaiono in tutte le scomposizioni
(III) moltiplicare tra loro questi fattori scelti con l'esponente più basso.
Ad es.


Per calcolare il Massimo Comune Denominatore tra due o più numeri, si esegue la scomposizione in fattori primi dei numeri assegnati poi si calcola il prodotto dei fattori comuni, ciascuno ciascuno elevato all'esponente più basso.
minimo comune multiplo m.c.m.
Il minimo comune multiplo tra due o più numeri è il più piccolo dei i loro multipli comuni.
Alcune regole si possono riconoscere immediatamente
• l'm.c.m. tra due numeri primi tra di loro è il prodotto dei numeri
stessi ad es.
mcm(5;6)=30
• assegnati due o più numeri, se uno di essi è multiplo degli altri,
quel numero è l'm.c.m. ad es.
mcm(3;4;12)=12
• assegnati tre o più numeri, l'm.c.m. può essere cercato trascurando
i numeri che sono divisori di altri numeri assegnati
mcm(3;6;8)=mcm(6,8)=24
per i numeri piccoli l'm.c.m. può essere constatato direttamente per i
numeri più grandi bisogna applicare la seguente procedura:
(I) scomporre i numeri dati in fattori primi, evidenziando le potenze;
(II) individuare tutti i fattori primi, comuni e non comuni alle diverse
scomposizioni;
(III) moltiplicare tra loro questi fattori, elevati alle potenze di esponente
più alto. Ad es.

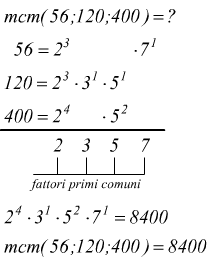
Il minimo comune multiplo tra due o più numeri si ottiene eseguendo la scomposizione in fattori primi dei numeri assegnati e si calcola il prodotto dei fattori primi comuni e non comuni, ciascuno elevato all'esponente più alto.
Se già si conosce il M.C.D. tra due numeri a e b è facile calcolare l'm.c.m.;
basta usare la formula 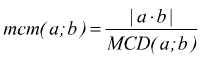
Metodo di Euclide per il calcolo dell' M.C.D.
Per trovare l'M.C.D. di due numeri si divide il maggiore per il minore; se il resto della divisione è zero, se cioè il primo numero è divisibile per il secondo, questo è l'M.C.D. dei due numeri assegnati. Se invece il resto non è nullo, si divide il numero minore per tale resto, e così via fino ad arrivare al resto uguale a zero.. L'ultimo resto non nullo è l'M.C.D. cercato.
Ad es. MCD(143;52)
Iniziamo dividendo il maggiore dei due numeri per l'altro
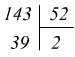
visto che il resto non è nullo si divide il divisore 52 per il resto 39
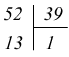
notiamo che il resto è ancora diverso da zero; dividiamo il divisore 39 per il resto 13
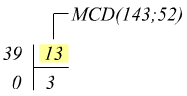
ora che si è ottenuto un resto nullo, possiamo dire che 13 (l'ultimo resto non nullo) è l'MCD cercato.
Il metodo di Euclide può essere facilmente automatizzato attraverso il seguente algoritmo
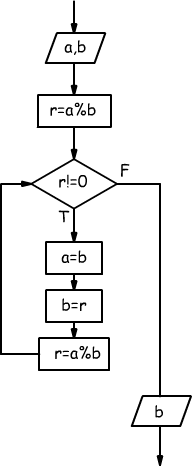
MCD(int a,int b){
//r=resto della divisione a/b
int r=a%b;
//continua a dividere
// finchè il resto non è nullo
while(r!=0){
a=b;
b=r;
r=a%b;
}
//risultato
return b;
}
su questa pagina, è possibile effetuare il calcolo dell'Massimo Comune Divisore anche con più numeri.
 edutecnica
edutecnica