Disequazioni frazionarie
Le disequazioni in cui l'incognita appare in almeno un denominatore dei
termini che la compongono vengono chiamate disequazioni frazionarie o anche
disequazioni razionali.
In generale una disequazione frazionaria può sempre essere ridotta ad una
disequazione dove al primo membro si ha una frazione algebrica e al secondo
membro zero.
Ad esempio
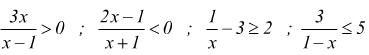
sono tutte disequazioni frazionarie che possono essere ricondotte alle seguenti
quattro forme: (considerando il simbolo ∨ cioè "oppure")
Da notare come la prima nostra preoccupazione sia quella di non far rientrare
nell'insieme delle soluzioni dei valori che possano violare le condizioni
di esistenza (C.E.) della frazione; cioè valori che portino il denominatore
alla condizione D(x)=0.
Per rendere più rapida ed agevole la risoluzione di una disequazione frazionaria
si può ricorrere alla rappresentazione grafica.
Segnati su una retta, su cui viene fissato un sistema di ascisse i punti
in cui si annullano numeratore N(x) e denominatore D(x) della frazione algebrica,
in corrispondenza dei singoli intervalli si indica il segno che in ciascuno
di essi compete al numeratore e al denominatore.
Dall'esame del grafico si rileva quali sono gli intervalli in cui i termini
della frazione algebrica hanno segni tali da soddisfare la disequazione.
Normalmente si conviene di segnare con un tratto continuo gli intervalli
in cui i termini della frazione sono positivi, e con una linea tratteggiata
quelli in cui i termini sono negativi.
Si devono escludere (come è ovvio) i valori di x che annullano il denominatore.
Il procedimento si può così riassumere:
1 Si studiano il segno del numeratore ed il
segno del denominatore della frazione algebrica al primo membro della disequazione.
2 Si disegna un grafico riassuntivo del segno
del numeratore e del denominatore e si deduce in base alla regola dei segni
della divisione il segno del loro rapporto.
3 Dallo schema del segno della frazione algebrica
si deducono le soluzioni della disequazione.
Un esempio di applicazione del procedimento risolutivo è il seguente:
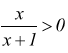
passo 1
Il numeratore N(x) è positivo quando x > 0.
Il denominatore D(x) è positivo quando x+1 > 0 cioè per x > -1.
passo 2
Adesso disegnamo lo schema riassuntivo del numeratore N e del denominatore
D.
● per x < -1 il numeratore (x) e il denominatore
(x+1) sono concordi negativi (-) quindi il loro rapporto è positivo (+).
● per -1 < x < 0 il numeratore e il
denominatore sono di segno discorde quindi il loro rapporto è negativo (-).
● per x > 0 il numeratore e il denominatore
sono di segno concorde positivo (+) quindi il loro rapporto è positivo (+).
passo 3
La disequazione 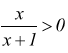è
verificata quando la frazione algebrica 
è
positiva cioè per
e si legge x minore di -1 oppure x maggiore di 0.
La condizione di esistenza della frazione x ≠ -1 è rispettata perchè
tale valore non appartiene all'insieme delle soluzioni.
Maggiore attenzione richiedono le disequazioni dove appare il segno di maggiore o uguale (≥) o minore o uguale (≤) in tal caso non ci devono essere ambiguità nel rispettare le condizioni di esistenza della frazione algebrica. Ad es.
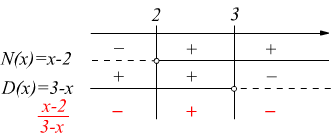
● per x < 2 il numeratore e il denominatore
sono di segno discorde quindi il loro rapporto è negativo (-).
● per 2 < x < 3 il numeratore e il
denominatore sono di segno concorde positivo (+) quindi il loro rapporto
è positivo (+).
● per x > 3 il numeratore e il denominatore
sono di segno discorde quindi il loro rapporto è negativo (-).
La disequazione è
verificata quando la frazione algebrica 
è positiva o nulla, cioè per
La soluzione x=2 può essere accettata perchè annulla il numeratore e dunque l'intera frazione algebrica, la soluzione x=3 deve essere esclusa perchè x ≠ 3 è condizione di esistenza della frazione algebrica stessa, perchè annulla il suo denominatore.
Disequazioni frazionarie di secondo grado
Le disequazioni frazionarie che presentano al numeratore e/o al denominatore
polinomi di secondo grado si possono risolvere con un procedimento analogo
a quello appena visto per le disequazioni frazionarie di primo grado.
Considerando che un polinomio di secondo grado può spesso essere ricondotto
al prodotto di due binomi possiamo avvalerci dello studio
del segno del prodotto e dello studio
grafico del segno del trinomio di secondo grado che avevamo precedentemente
visto. Ad es.
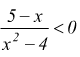
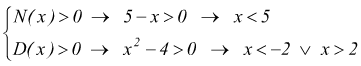
infatti y=x2-4 rappresenta una parabola con la concavità rivolta verso l'alto che risulta maggiore di zero per valori esterni all'intervallo -2 < x < 2.
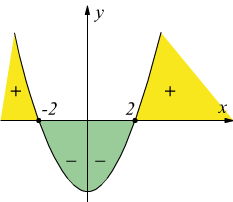facciamo
lo schema 
da cui si vede come la frazione sia negativa e quindi soddisfatta negli insiemi di valori
