Disequazione di secondo grado
Una disequazione di secondo grado è una disequazione riconducibile ad una delle seguenti forme canoniche:

come si vede, al primo membro appare sempre un polinomio di secondo grado
nella variabile incognita x; generalmente questa espressione viene chiamata
trinomio di secondo grado e prevede l'eventuale presenza delle due radici
(o zeri) x1 ed x2 che annullano il trinomio stesso.
Queste radici (se esistono) possono essere ottenute rapidamente con la nota
formula risolutiva del trinomio di secondo grado

l'espressione iniziale del trinomio assegnato può dunque essere rimaneggiata nel seguente modo:
![]()
arrivati a questo punto si può procedere per via algebrica studiando il segno del prodotto $a(x-x_1)(x-x_2)$ oppure analizzando l'espressione dal punto di vista grafico, dato che la scrittura $y=ax^2+bx+c$ , in geometria analitica, risulta essere rappresentativa di una parabola che sul piano cartesiano xy ha intersezione con l'asse delle x proprio in corrispondenza delle due radici x1 ed x2.
Studio del segno del prodotto
Supponiamo che venga assegnata la disequazione
![]()
ci si chiede per quali valori della variabile x la disequazione risulta soddisfatta. Ricaviamo le radici del trinomio di secondo grado presente al primo membro
 otteniamo
otteniamo
 da
cui
da
cui

possiamo ora riformulare la disequazione nel seguente modo

Il fatto che la disequazione venga soddisfatta o meno dipende dai valori assunti dai due operandi A e B al variare di x : il coefficiente 2 non interviene in questa discussione perchè esso è sempre positivo. Ci chiediamo semplicemente allora quando $A=x-3$ è maggiore di zero e quando $$B=x+5/2$$ è maggiore di zero.

ora, rappresentiamo i valori 3 e $$-5/2$$ su una retta orizzontale orientata e per indicare i segni di $(x-3)$ e di $$(x-5/2)$$ disegniamo con linea a tratto continuo gli intervalli con segno positivo (segno +) e con linea tratteggiata quelli con segno negativo (segno -)

tenendo poi conto delle regole del segno della moltiplicazione 
sarà possibile individuare gli intervalli in cui viene verificato il prodotto A·B.

come si vede dal disegno il prodotto $$(x-3)(x+5/2)$$ è positivo solo per x<-5/2 oppure per x>3, l'insieme delle soluzioni può essere indicato come

Studio grafico
Le disequazioni di secondo grado possono anche essere risolte per via
grafica, studiando il segno del trinomio di secondo grado nella forma $ax^2+bx+c$.
Questa forma canonica, può essere infatti associata alla funzione $y=ax^2+bx+c$
che descrive una parabola
sul piano cartesiano.
Nella disequazione assegnata, possiamo sempre riportarci al caso in cui
il coefficiente a di $x^2$ sia positivo, moltiplicando per $-1$ e
cambiando verso al segno della disequazione.
Se ipotizziamo a>0 la parabola associata alla disequazione avrà la concavità
rivolta verso l'alto e potranno presentarsi soltanto tre casi: in cui il
valore del discriminante $Δ=b^2-4ac$ svolge un ruolo cruciale:

Se Δ > 0 il trinomio risulta
positivo negli intervalli esterni ad x1 ed x2 cioè quando x<x1 ∨ x>x2
nullo per x=x1 ∨ x=x2
negativo nell'intervallo interno tra x1 ed x2 cioè per x1<x<x2 .

Se Δ = 0 il trinomio risulta
positivo per ogni valore reale di x diverso da x1 (con x1=x2)
nullo per x=x1 (con x1=x2) .

Se Δ < 0 il trinomio risulta sempre positivo .
esempio 1 Δ>0 a>0
![]()

il trinomio ammette le due radici x1=2 ed x2=3 e può essere associato ad una parabola con la concavità rivolta verso l'alto (a=1>0) che interseca l'asse delle ascisse in corrispondenza delle due radici trovate.
Dal disegno si vede che y>0 solo per x<2 oppure x>3, noi allora scriveremo che l'insieme delle soluzioni è x<2 ∨ x>3.
esempio 2 Δ>0 a<0
![]()
moltiplicando entrambi i membri per -1 può essere invertito il segno di disuguaglianza
![]()

le soluzioni del trinomio (a cui manca il termine noto) sono evidentemente x1=0 ed x2=5
la soluzione della disequazione è evidentemente 0 ≤ x ≤ 5 perchè soltanto in questi casi la curva di equazione y=x2-5x è minore o uguale a 0.
esempio 3 Δ=0 a<0
![]()
moltiplicando entrambi i membri per -1 può essere riportata alla forma in cui a>0:
![]()

che ammette le due radici reali coincidenti x1=x2=3
dal disegno si vede come la x2-6x+9 non è mai minore di 0, ma è uguale a 0 solo per x=3, la soluzione, è dunque quest'unico valore.
esempio 4 Δ=0 a>0
![]()
il trinomio ammette le due radici reali coincidenti x1=x2=3 il coefficiente a>0 la curva ha concavità rivolta verso l'alto.
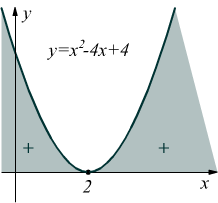
ma la disequazione chiede per quali valori di x il trinomio è strettamente maggiore di 0. Questo è vero per ogni valore di x eccetto che per x=2 dove il valore del trinomio è 0. la soluzione sarà dunque ℜ-[2] dove con ℜ indichiamo l'insieme dei numeri reali.
esempio 5 Δ<0 a>0
![]()

in tal caso a=1>0 ma Δ=-3 la parabola che descrive il trinomio non tocca l'asse delle ascisse x ed il trinomio assume sempre valori positivi ∀x (per ogni valore di x).
Se la domanda posta dalla disequazione è per quali valori di x il trinomio diventa negativo, la risposta è necessariamente: impossibile. Cioè l'insieme delle soluzioni è vuoto (∅).
 edutecnica
edutecnica