Integrali Curvilinei
Integrale curvilineo del tipo
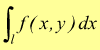

La funzione a due variabili
![]() [I]
[I]
rappresenta geometricamente , una superficie S i cui punti hanno coordinate x,y,z che la soddisfano.
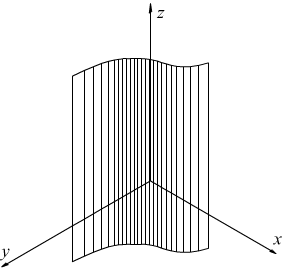
La funzione
y=ϕ(x) [II]
interpretata geometricamente, nel piano rappresenta una linea l, interpretata
nello spazio, rappresenta una superficie cilindrica.
Dato che nella [II] si intende z qualunque, l'intersezione tra la superficie
S [I] ed il cilindro [II] genera la linea spaziale γ.

Se x ed y non sono indipendenti ma sussiste la [II] allora si può dire
che la funzione z=f(x,y) rappresenta in generale una linea sghemba γ.
La forma [I] grazie alla [II] diventa, allora, una funzione ad una sola
variabile.
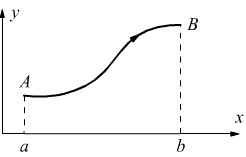
![]()
Nella y=ϕ(x); ammettiamo a≤x≤b.
Se F(x) integrabile, esiste l'integrale definito
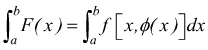 [III]
[III]
Questo integrale pu anche essere scritto nella forma
![]() [IV]
[IV]
chiamato integrale curvilineo.
Bisogna sottolineare che nella forma [IV]
x ed y non sono variabili indipendenti, ma legate dalla relazione y=ϕ(x)
che l'equazione della linea l che unisce i due punti A e B.
In base a queste osservazioni l'integrale curvilineo risulta una generalizzazione
dell'integrale definito ordinario; esso va quindi calcolato ponendo:
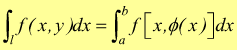 [V]
[V]
Questa definizione vale anche in senso inverso, dunque per l'integrale definito
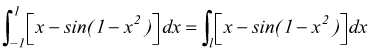
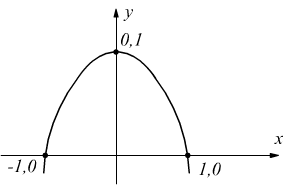
avendo posto y=1-x2 che l'equazione della parabola che
interseca l'asse x in -1 ed 1.

Viceversa, l'integrale curvilineo
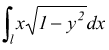
dove l l'arco di circonferenza ![]() che
unisce i punti A(1,0) e B(0,1) si può risolvere per la [V]
che
unisce i punti A(1,0) e B(0,1) si può risolvere per la [V]
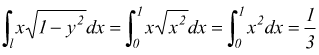
Esempio:
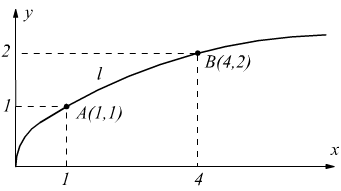
A(1,1) e B(4,2) sono due punti del piano xy che possono essere uniti
da infinite linee. Fra le tante, scegliamo l'arco di parabola x=y2
e calcoliamo l'integrale curvilineo:
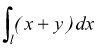
per la [V] essendo x=y2 → ![]() si
ha:
si
ha:
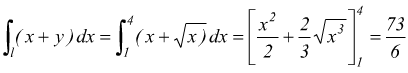
Notiamo come allo stesso risultato ci si può arrivare esprimendo la funzione integrando in y invece che in x usando per il differenziale dx il seguente accorgimento:
 quindi
quindi
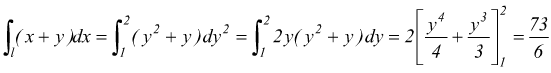
altro esempio:
Calcolare l'integrale curvilineo 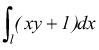 con
y=ex inoltre con 0≤x≤1 per la [V] si ha
con
y=ex inoltre con 0≤x≤1 per la [V] si ha
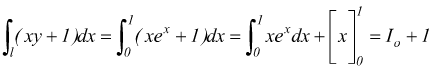
 quindi
quindi
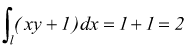
Dagli esempi si conclude che per la soluzione possono essere usate le due opzioni
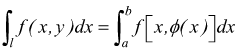 [VI]
oppure
[VI]
oppure
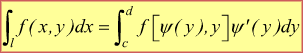 [VII]
[VII]
Integrale curvilineo del tipo
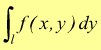
Anche l'espressione ![]() [VIII]
[VIII]
è una generalizzazione dell'integrale definito ordinario. Per
risolverla, occorre l'equazione della linea l ed i limiti entro cui
varia la variabile indipendente. Quindi:
a) se l'equazione di l del tipo x=ψ(y) con c≤y≤d si ha
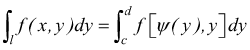 [IX]
[IX]
b) se l'equazione della linea l y=ϕ(x) con a≤x≤b si ha
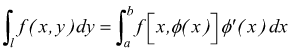 [X]
[X]
Esempio:
Consideriamo i punti A(1,1) e B(4,2) uniti dall'arco di parabola di
equazione x=y2. Calcolare l'integrale curvilineo
![]()
Per la [IX] avremo 
Integrale curvilineo del tipo
![]()
Sulla stessa linea l del piano xy di equazione
y=ϕ(x) con a≤x≤b
x=ψ(y) con c≤y≤d
definiamo due funzioni z=A(x,y) e z=B(x,y) entrambe continue. Per la prima funzione deve essere valida la [V] e per la seconda la [IX] cio deve sussistere
 e
e 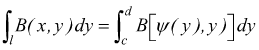
sommando membro a membro

dato che la linea di integrazione la stessa per entrambi gli integrali curvilinei

in modo analogo si può scrivere

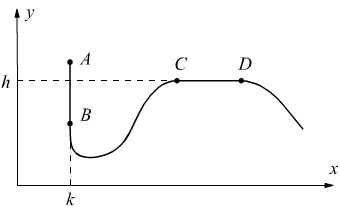
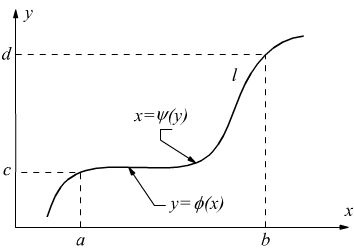
Esiste l'eventualit che la linea l, o alcuni suoi tratti siano paralleli
all'asse x o all'asse y. Ad es. in figura rappresentata una linea
parallela nel tratto AB all'asse y e nel tratto CD parallela all'asse
x. Dato che gli integrali curvilinei hanno tutte le propriet degli
integrali definiti ordinari (si riducono ad essi) allora possiamo scrivere

ma nel tratto AB x=cost. → dx=0
e nel tratto CD y=cost. → dy=0; dunque
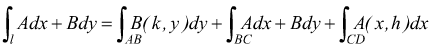
Circuitazione
Un integrale curvilineo, cambia segno ma non cambia valore assoluto, se la linea di integrazione viene percorsa nei due sensi opposti:questa una propriet degli integrali definiti ordinari ai quali si riducono gli integrali curvilinei.

 questo
perch per l'integrale definito
questo
perch per l'integrale definito
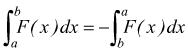
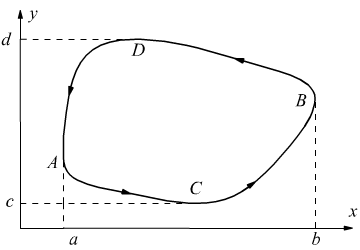
Un discorso a parte merita un cammino di integrazione costituito da una linea chiusa
Se si vuole indicare un senso di percorrenza si dovrebbe dire
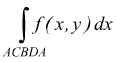 se
il senso di percorrenza quello indicato dalla freccia
se
il senso di percorrenza quello indicato dalla freccia
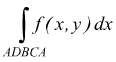 se
il senso di percorrenza quello opposto a quello della freccia
se
il senso di percorrenza quello opposto a quello della freccia
Di solito un integrale curvilineo esteso ad una linea chiusa viene
indicato col simbolo ![]() e
si legge "integrale esteso alla linea chiusa
l" oppure "circuitazione" con
questo simbolismo non si privilegia nessun senso di percorrenza della
linea l.
e
si legge "integrale esteso alla linea chiusa
l" oppure "circuitazione" con
questo simbolismo non si privilegia nessun senso di percorrenza della
linea l.
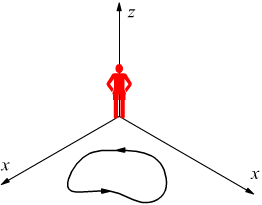
Normalmente si assume come convenzionalmente positivo, quello giudicato antiorario da un osservatore al quale l'asse z entri dai piedi ed esca dalla testa quando esso e posto in piedi sul piano xy e si intende che gli assi xy siano orientati (come al solito) in modo tale che si assista ad una rotazione antioraria dell'asse x per farlo sovrapporre all'asse y.
Quando allora viene assegnato il calcolo di un integrale curvilineo esteso ad una linea chiusa bisogna operare in modo che la linea venga percorsa in senso positivo.
Ad es.:
Calcola  lungo
la circonferenza di equazione x2+y2=4.
lungo
la circonferenza di equazione x2+y2=4.
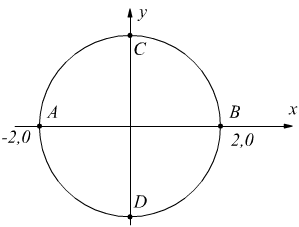
Dall'equazione della linea y2=4-x2 si ha:
![]() eq.
arco ADB
eq.
arco ADB
![]() eq.
arco ACB
eq.
arco ACB
Lungo l'arco ADB 
Lungo l'arco ACB  Partendo
da A e percorrendo la circonferenza in senso positivo deve essere
Partendo
da A e percorrendo la circonferenza in senso positivo deve essere

procedendo per sostituzione x=2sin(t) → dx=2cos(t)dt

Se avessi percorso la circonferenza in questione in senso contrario avremmo , invece, trovato -4π.
Linea di integrazione in coordinate parametriche
Se la linea di integrazione viene assegnata in coordinate parametriche
x=x(t) ; y=y(t) con t1≤t≤t2 .
eliminando la t fra le relazioni soprascritte si ottiene l'equazione della linea. Inoltre sappiamo che ad ogni valore di t, compreso tra t1 e t2; in particolare se per t=t1 e t=t2 si ottengono rispettivamente i punti A e B e se in tutto l'intervallo (t1,t2) le equazioni precedenti sono derivabili, allora :

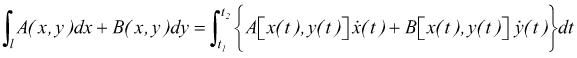
Esempio: Calcola l'integrale
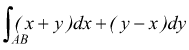
lungo la linea che unisce A(1,1) e B(4,2) di equazioni parametriche
x=2t2+t+1
y=t2+1
Determiniamo i valori di t che individuano A(1,1) e B(4,2). Nel caso
di A(1,1) occorre individuare il valore di t per il quale contemporaneamente
2t2+t+1=1 e t2+1=1 → la soluzione comune
t=0. Nel caso di B(4,2)
2t2+t+1=4 e t2+1=2 → t=1 la soluzione che
verifica entrambe le equazioni e pertanto individua il punto B.
Dalle equazioni parametriche si deduce: dx=(4t+1)dt e dy=2tdt

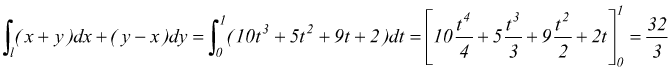
Interpretazione fisica dell'integrale curvilineo
Sul piano xy ipotizziamo una linea l di equazioni parametriche
x=x(t) ; y=y(t) con t1≤t≤t2
Preso un punto P su l, si può definire il vettore ![]() di
posizione che ha punto di applicazione in O ed estremo in P quindi
di
posizione che ha punto di applicazione in O ed estremo in P quindi
![]()

dove ![]() il
versore (vettore unitario) indicativo l'asse x e
il
versore (vettore unitario) indicativo l'asse x e ![]() il
versore per l'asse y;incrementando t di Δt si ha
il
versore per l'asse y;incrementando t di Δt si ha
![]()
Il vettore :
![]()
la direzione di ![]() secante alla linea l. Al tendere di Δt a zero il punto Q tende
a P e la secante tende alla tangente in P; ne segue
secante alla linea l. Al tendere di Δt a zero il punto Q tende
a P e la secante tende alla tangente in P; ne segue
 poi
poi
![]() cio
cio
![]()
se la linea l viene assegnata in coordinate parametriche x=x(t) ed y=y(t). Ipotizzando che la linea l possa essere descritta dalla funzione y=y(x):

Ritornando alla forma differenziale:
A(x,y)dx+B(x,y)dy [XI]
ipotizziamo A(x,y) e B(x,y) definite in ogni punto della linea l. Allora, queste due funzioni si possono interpretare come le componenti di un vettore
![]()
allora la [XI] viene generata dal prodotto scalare dei vettori

se il vettore v fosse una forza il prodotto scalare visto darebbe luogo al lavoro elementare dL compiuto dalla forza spostando il suo punto di applicazione dr lungo l.
![]() integrando
quest'ultima su tutta la linea abbiamo
integrando
quest'ultima su tutta la linea abbiamo

che rappresenta il lavoro compiuto dalla forza ![]() spostando
il suo punto di applicazione lungo tutta la linea l. In particolare,
se
spostando
il suo punto di applicazione lungo tutta la linea l. In particolare,
se ![]() fosse la forza
che agisce sull'unit di massa, l'integrale:
fosse la forza
che agisce sull'unit di massa, l'integrale:
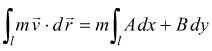
Se ![]() fosse la forza
che agisce sull'unit di carica elettrica, l'integrale
fosse la forza
che agisce sull'unit di carica elettrica, l'integrale
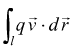
Sarebbe il lavoro compiuto dalla forza ![]() sulla
carica q per spostarla lungo tutta la linea l.
sulla
carica q per spostarla lungo tutta la linea l.
Interpretazione geometrica dell'integrale curvilineo
L'integrale curvilineo ha anche un significato geometrico Facendo i soliti presupposti, cio che esista un legame y=ϕ(x) oppure x=ψ(y) e la linea γ di equazione z=f(x,y)=f[x,ϕ(x)] inoltre ipotizziamo a≤x≤b e c≤y≤d.
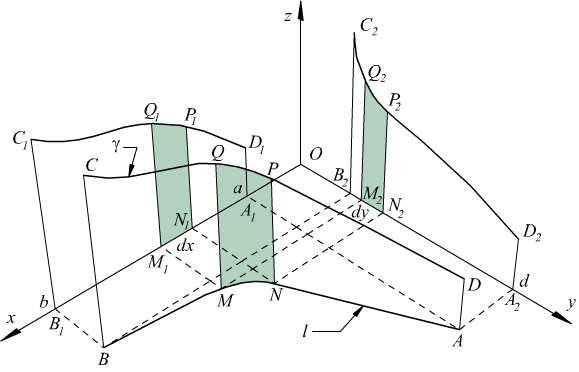
La superficie delimitata da l, γ ed i segmenti BC ed AD, si proietta
nel trapezoide A1B1C1D1
del piano zx e nel trapezoide A2B2C2D2
del piano yz; l'elemento dl ha per proiezioni sui due assi x ed y rispettivamente
gli elementi dx e dy.
La striscia MNPQ si proietta nelle due proiezioni M1N1P1Q1
ed M2N2P2Q2 dei piani xz
ed yz. Queste ultime due proiezioni hanno la caratteristica che : per
qualsiasi coppia x,y di dl la quota z=f(x,y) la stessa per la striscia
MNPQ e per le sue due proiezioni. Si verifica che per un certo x,y di
dl.
f(x,y)dx l'area della proiezione M1N1P1Q1.
f(x,y)dy l'area della proiezione M2N2P2Q2.
f(x,y)dl l'area della striscia MNPQ.
Se suddividiamo la linea l in infiniti elementi dl, sommando le infinite aree che si ottengono
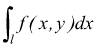 l'area del trapezoide A1B1C1D1.
l'area del trapezoide A1B1C1D1.
 l'area del trapezoide A2B2C2D2.
l'area del trapezoide A2B2C2D2.
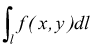 l'area della superficie ABCD.
l'area della superficie ABCD.
In quest'ultimo caso bisogna ricordarsi che
![]() se
l ha equazione y=ϕ(x) con a≤x≤b
se
l ha equazione y=ϕ(x) con a≤x≤b
![]() se
l ha equazione x=ψ(x) con c≤y≤d
se
l ha equazione x=ψ(x) con c≤y≤d
![]() se
l ha equazione parametrica x=x(t) ; y=y(t).
se
l ha equazione parametrica x=x(t) ; y=y(t).
Ne consegue che se l viene assegnata in forma cartesiana
 [XII]
[XII]
mentre se viene assegnata in forma parametrica
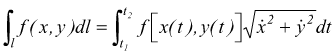 [XIII]
[XIII]
Esempio:
Calcola 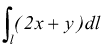 lungo
il percorso pi corto che unisce i punti A(3,4) e B(4,3) della linea
l di equazione x2+y2=25.
lungo
il percorso pi corto che unisce i punti A(3,4) e B(4,3) della linea
l di equazione x2+y2=25.

Possiamo trattare la circonferenza x2+y2=25 con
le sue equazioni parametriche
x=5cosθ → dx=-5sinθ·dθ
y=5sinθ → dy=5cosθ ·dθ
Troviamo I valori di θ che individuano I punti A e B . Per individuare A(3,4) deve essere simultaneamente:

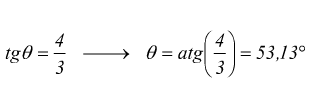
In modo analogo per individuare B(4,3)

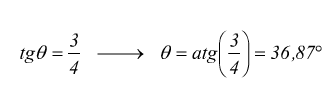
La strada pi corta quella che partendo da A(θ1=53,13 ) conduce a B(θ2=36,87 ) quindi l'integrale diventa:
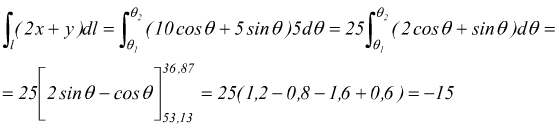
NB:dl viene in questo caso ottenuto osservando che
![]()
Lunghezza di una linea curva piana
La [XII] e la [XII] diventano per f(x,y)=1

se l'equazione assegnata in forma parametrica y=ϕ(x) o x=ψ(x) si ha
 [XIV]
[XIV]
se l'equazione assegnata con le sue equazioni parametriche x=x(t) ed y=y(t)
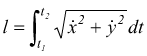 [XV]
[XV]
Esempio: trovare la lunghezza della linea curva piana le cui equazioni parametriche sono:
 tra
i punti corrispondenti
tra
i punti corrispondenti 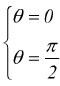
Applicando la [XV] 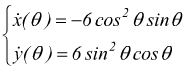 ottenendo
ottenendo
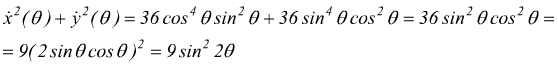
avremo

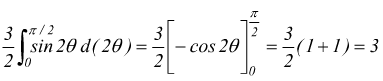
Integrali curvilinei indipendenti dal percorso di integrazione

Consideriamo due punti: P e Q sul piano xy uniti dal cammino di integrazione l1 e l'integrale di linea

poi consideriamo l'integrale
 calcolato
sul cammino l2 sempre congiungete P a Q.
calcolato
sul cammino l2 sempre congiungete P a Q.
Si possono considerare anche altri percorsi l3, l4,.. , ln che congiungono P a Q; se risulta:
I1=I2=I3= =In
Pu essere ragionevole pensare che l'integrale non dipenda dal percorso di integrazione.Si può dimostrare che se
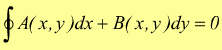
cio se la circuitazione della forma differenziale A(x,y)dx+B(x,y)dy nulla allora l'integrale
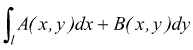
dove l una qualsiasi linea che unisce i due punti P e Q non dipende
da l, ma solo dagli estremi Pe Q.
Infatti basta pensare di percorrere l1 in senso positivo
(da P a Q) ed l2 in senso negativo (da Q a P) e si ha:
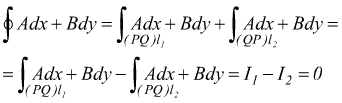
Questo vale per gli integrali curvilinei la cui funzione integranda
A(x,y)dx+B(x,y)dy un differenziale esatto.
Affinch l'espressione A(x,y)dx+B(x,y)dy sia un differenziale esatto,deve
esistere una funzione z=f(x,y) tale che
 se
queste sono valide, si può osservare che
se
queste sono valide, si può osservare che
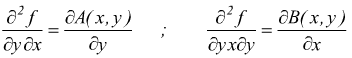
Per cui, la forma A(x,y)dx+B(x,y)dy un differenziale esatto se si verifica:
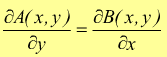
L'integrale curvilineo di un differenziale esatto non dipende dal percorso di integrazione ma dagli estremi di tale percorso.

Integrale curvilineo nello spazio - lunghezza di una linea sghemba
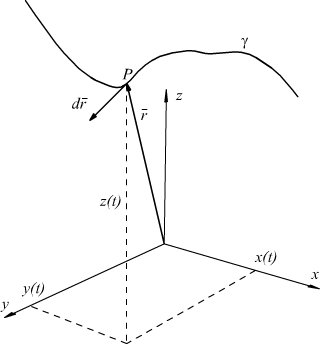
Le
equazioni parametriche di una linea γ nello spazio tridimensionale
sono:
x=x(t)
y=y(t) z=z(t)
con t1 ≤ t ≤ t2. Nei punti di questa linea
supponiamo siano definite tre funzioni continue
A(x,y,z); B(x,y,z); C(x,y,z) [XVI]
Un qualsiasi punto P di γ ha coordinate x(t), y(t), z(t). Queste
coodinate possono essere interpretate come le componenti del vettore
posizione ![]() quindi
risulta essere
quindi
risulta essere
![]() [XVII]
[XVII]
le tre funzioni [XVI] a loro volta possono interpretarsi come le componenti di un vettore definito come
![]()
differenziando entrambi i membri della [XVII] otteniamo
![]()
tangente in P alla linea γ e avente modulo
![]()
il prodotto scalare tra ![]() e
e
![]() ci
permette di ottenere la seguente forma differenziale lineare:
ci
permette di ottenere la seguente forma differenziale lineare:
![]() [XVIII]
[XVIII]
Questo prodotto scalare, fornisce il lavoro compiuto dal vettore ![]() per
lo spostamento infinitesimo
per
lo spostamento infinitesimo ![]() lungo
la linea γ del punto di applicazione di
lungo
la linea γ del punto di applicazione di ![]() ;
cio :
;
cio :
![]()
Per ottenere il lavoro compiuto lungo tutta la linea γ dobbiamo fare l'integrale:
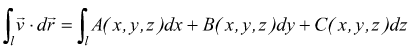
Il modo meno faticoso per calcolare quest'ultimo integrale quello di renderlo funzione del parametro t.
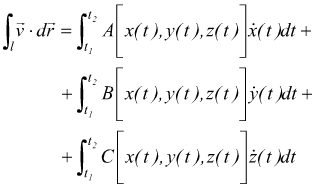
Il prodotto scalare tra due vettori, si sa che dato dal prodotto dei moduli dei due vettori per il coseno dell'angolo compreso tra loro.
![]()
quindi se per ipotesi ![]() ed
tangente a γ in P (α=0) si ha
ed
tangente a γ in P (α=0) si ha
 fornisce
la lunghezza della linea γ
fornisce
la lunghezza della linea γ
Se γ viene data in forma parametrica
![]() quindi
quindi
![]()
Se invece γ viene assegnata in forma cartesiana con y=ϕ(x) e z=ψ(x) a≤x≤b si ha:
 con
con 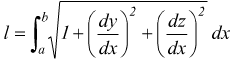
 edutecnica
edutecnica