Trasmissione del calore
Il trasferimento del calore è un fenomeno molto diffuso che avviene sempre quando due corpi si trovano a temperature diverse.
Lo studio del trasferimento del calore, ha come obiettivo la descrizione delle grandezze che influenzano lo scambio di calore ed in che modo lo influenzano. In generale, oltre alla differenza di temperatura, senza la quale non ci sarebbe lo scambio termico, anche le caratteristiche fisiche e geometriche del sistema influenzano notevolmente la modalità e la quantità di calore scambiato. Il trasferimento di calore tra due corpi può avvenire attraverso tre meccanismi fondamentali: la conduzione, la convezione e l'irraggiamento. In molti casi si possono avere contemporaneamente due o tre meccanismi di scambio simultaneamente.
Conduzione
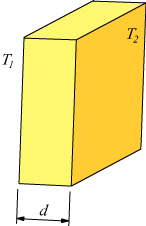
Consideriamo una parete solida
piana di spessore `d` in cui le due facce opposte si trovano
a temperature diverse.
Come detto, la differenza di temperatura è una condizione sufficiente affinché
si manifesti un trasferimento di calore.
Essendo la parete solida non si potranno verificare spostamenti di gruppi molecolari o di singole molecole.
Di conseguenza il calore viene trasmesso grazie ai moti vibrazionali delle molecole.
Nei metalli, caratterizzati dal fatto che gli elettroni dello strato di valenza possono muoversi
liberamente, sono proprio questi a determinare il trasferimento del calore.
Questo meccanismo di trasferimento del calore è chiamato conduzione.
La conduzione, non è comunque una esclusiva dei corpi solidi, ma si può verificare anche nei fluidi, a patto che non vi sia un flusso netto di materia, cioè, a patto che il fluido sia completamente fermo. Diversamente, insieme alla conduzione si verificheranno altri meccanismi di trasporto decisamente più significativi.
Equazione di Fourier per le pareti piane
L'equazione di trasferimento associata alla conduzione è l’equazione di Fourier, sviluppata nei primi decenni dell’800; nel caso di una parete piana semplice, essa si esprime come
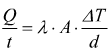
Q = quantità di calore trasferita [ J ]
t = tempo in secondi [s ]
ΔT = differenza di temperatura tra le due pareti [ °K ]
d = spessore della parete [ m ]
λ = conducibilità termica [ W/m°K ]
A = superficie della parete [ m2 ]
In fondo alla pagina viene riportata una tabella contenente il valore della conducibiltà termica di alcuni materiali.
Notiamo come il rapporto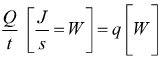 
sia
una energia specifica nell'unità di tempo che coincide dimensionalmente
con la potenza misurabile in watt. Da questo momento in poi troviamo comodo
indicare questo flusso di energia con la lettera `q`. Dunque
scriviamo
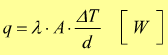Il
rapporto 
viene
definito gradiente termico.
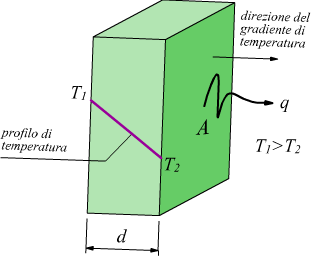
In generale, il gradiente di una grandezza è dato dal rapporto tra la differenza dei valori che la grandezza assume in due punti e la distanza tra i due punti. Il gradiente è una condizione sufficiente affinché si manifesti un trasferimento della grandezza in analisi, che avverrà nella stessa direzione del gradiente. Nel nostro caso, il gradiente termico è tale da trasferire il calore dalla faccia più calda a quella più fredda, mentre non c'è flusso termico in altre direzioni.
Il gradiente rappresenta anche l'inclinazione del cosidetto profilo di temperatura. ovvero la variazione di temperatura tra le due facce. Materiali che possiedono una elevata conducibilità presentano un piccolo gradiente termico, cioè la temperatura non varia di molto. Al contrario, i materiali isolanti a parità di calore trasportato e spessore della parete presentano elevate differenze di temperatura tra le facce opposte .
Equazione di Fourier per superfici piane composte
Consideriamo il sistema qui disegnato , costituito da una parete piana composta da tre materiali a conducibilità diversa. Le pareti estreme si trovano alla temperatura T1 e T2 , le singole pareti hanno
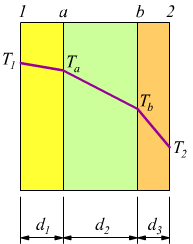
parete 1 : conducibilità λ1 spessore d1
parete 2 : conducibilità λ2 spessore d2
parete 3 : conducibilità λ 3 spessore d3
Non possiamo applicare l'equazione di Fourier per l'intera parete composta
perché le conducibilità dei tre materiali sono differenti.
Possiamo però applicare l'equazione di Fourier alle singole pareti ottenendo:
parete 1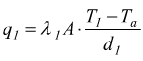 
parete 2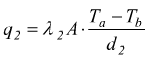 
parete 3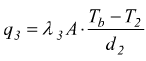 
in assenza di flussi di calore trasversali, possiamo affermare che 
riscriviamo le equazioni precedenti esplicitando le differenze di temperatura:
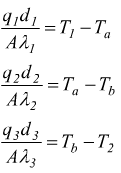
Sommando le tre equazioni membro a membro e sapendo che il calore trasferito attraverso le pareti è sempre uguale.
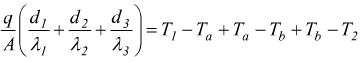
si conclude che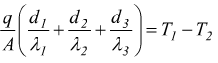 
da
qui, esplicitando il flusso di calore trasmesso si ha
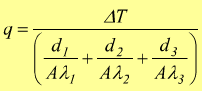
In questo modo può essere rimaneggiata l'equazione di Fourier per le pareti composte. In modo analogo al caso della parete semplice, il calore complessivamente trasferito dipende da una causa forzante, data dalla differenza tra le due temperature estreme (ΔT=T1-T2) divisa per una resistenza al trasferimento, in questo caso costituita da una resistenza complessiva, data dalla somma delle singole resistenze opposte da ogni parete.
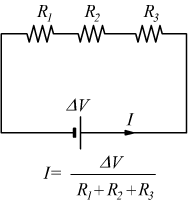
L'ultima formula mostra la stretta analogia tra i fenomeni elettrici ed il trasferimento di calore.
Come si vede anche dal disegno dove appare un circuito elettrico con tre resistenze in serie . La corrente che percorre il circuito è data dal rapporto tra la causa forzante che in questo caso è costituita dalla differenza di potenziale ΔV del generatore e la somma delle resistenze elettriche. Questa analogia, può già costituire una buona base per la definizione di una resistenza termica.
Equazione di Fourier per una superfice cilindrica
Un altro caso interessante di conduzione è quello che può avvenire attraverso una parete cilindrica come si vede dal disegno seguente
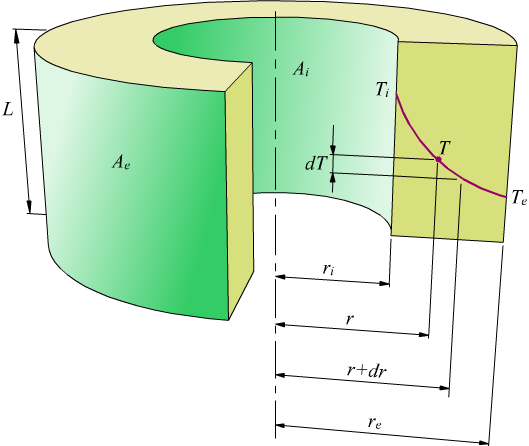
Tra la parete esterna e quella interna vi è una differenza di temperatura
che determina un trasferimento del calore.
Quello che distingue questo tipo di geometria da quella a parete piana è
il fatto che la superficie della parete cilindrica interna è diversa dalla
superficie cilindrica esterna. Infatti si ha
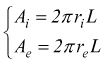
con L = lunghezza del cilindro
Ai = area della superficie interna
Ae = area della superficie esterna
ri = raggio interno
re = raggio esterno
Questo fatto impedisce l'applicazione della legge di Fourier così come
era stato fatto per la geometria piana. Possiamo superare il problema considerando
un elemento della parete cilindrica di spessore estremamente piccolo.
Nel disegno abbiamo indicato con dr questo spessore e con dT la relativa
variazione di temperatura. Se conosciamo qualche elemento di analisi matematica
sappiamo già che ci stiamo riferendo ad un differenziale, cioè ad una variazione
infinitesima della grandezza considerata, in alternativa al simbolo Δ
(delta) che indica invece una differenza finita. Per esempio, dr indica
una variazione infinitesima del rggio r.
Una variazione infinitesima, è una variazione estremamente piccola se confrontata
con i valori di re o ri o con la loro differenza Δr.
In modo analogo, dT indica una variazione di temperatura estremamente piccola
se confrontata alla variazione totale.
Tornando alla nostra parete cilindrica elementare, essendo la differenza
tra raggio interno e raggio esterno infinitesima sull'elemento considerato,
sarà trascurabile anche la differenza tra la superficie della parete esterna
e quella interna.
per cui essendo dr molto piccolo se paragonato ad r si ha 
per ricavare l'espressione relativa all'intero spessore della parete è necessario effettuare l'integrale definito tra le condizioni estreme ottenendo
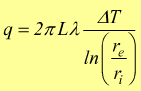
| Materiale | λ [W/m°K] | ρ [kg/m3] |
| diamante | 1600 | 3500÷3600 |
| argento | 460 | 10490 |
| rame | 390 | 8930 |
| oro | 320 | 19250 |
| alluminio laminato | 290 | 2750 |
| ottone | 111 | 8500 |
| platino | 70 | 21400 |
| acciaio | 52 | 7850 |
| piombo | 35 | 11300 |
| acciaio inox | 17 | 7480÷8000 |
| quarzo | 8 | 2500÷2800 |
| ghiaccio | 2,20÷2,50 | 917 |
| vetro pyrex | 1,4 | 2,22 |
| vetro laminato | 1 | 2500 |
| laterizi (mattoni) | 0,90÷0,72 | 2000÷1800 |
| vetro da finestra | 0,721 | 2500 |
| asfalto | 0,70 | 2100 |
| cartone ondulato | 0,65 | 100 |
| acqua distillata | 0,60 | 1000 |
| cartone catramato | 0,5 | 1600 |
| mattoni di kaolino | 0,35 | 950 |
| polietilene | 0,387 | 27 |
| glicole etilenico | 0,25 | 1110 |
| cartone bitumato | 0,23 | 1100 |
| laterizi (forati) | 0,25 | 600 |
| polipropilene | 0,22 | 920 |
| cartongesso | 0,21 | 900 |
| plexiglas | 0,19 | 1180 |
| carta e cartone | 0,14÷0,22 | 700÷1150 |
| legno (quercia) | 0,18 | 750 |
| idrogeno | 0,172 | |
| bitume | 0,17 | 1200 |
| polistirene | 0,17 | 1100 |
| legno asciutto | 0,15÷0,27 | 400÷750 |
| olio minerale | 0,15 | 900÷930 |
| neve | 0,12 | |
| legno (conifere) | 0,10 - 0,12 | 400 |
| pietra pomice | 0,08 | |
| vermiculite espansa | 0,07 | 90 |
| cartone ondulato | 0,065 | 100 |
| neve | 0,060 | |
| canna palustre | 0,055 | 190 |
| trucioli di legno | 0,050 | 100 |
| lana di roccia | 0,052 | |
| sughero | 0,052 | 200 |
| granuli di sughero | 0,050 | 100 |
| vetro cellulare (120) | 0,041 | 120 |
| lana di pecora | 0,040 | 25 |
| polistirolo estruso (XPS) | 0,040 | 20÷30 |
| polistirolo espanso (EPS) | 0,035 | 20÷30 |
| poliuretano espanso | 0,034÷0,032 | 25÷50 |
| aria secca | 0,026 | 1,2 |