Vettori e matrici in Economia

I vettori, già introdotti nelle pagine di fisica e matematica sono stati definiti come delle entità geometriche, descrivibili come segmenti orientati caratterizzati da una lunghezza (modulo o intensità), una direzione ed un verso. Questa definizione descrive bene alcune grandezze fisiche che si manifestano nello spazio bidimensionale o tridimensionale (forza, velocità, etc..).

Nel disegno seguente il vettore OP può essere rappresentato dal segmento orientato di estremo iniziale O(0,0) ed estremo finale P(x₁,y₁).

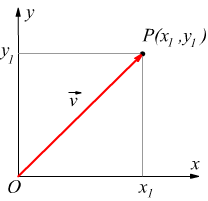
Se x₁ ed y₁ sono le coordinate di P, per indicare il vettore

useremo il simbolo

I numeri reali x₁ ed y₁ prendono il nome di coordinate scalari del vettore .

Scalare è un termine derivato dalla fisica.
E' noto che alcune grandezze fisiche, come il tempo o la temperature possono essere rappresentate da un numero reale che indica la misura della grandezza in questione rispetto ad una certa unità di misura, mentre altre , come le forze, possono essere rappresentate da vettori; da qui la distinzione tra grandezze scalari e vettoriali. Le coordinate scalari di un vettore sono anche dette componenti del vettore.
Se consideriamo a e b due numeri reali, valgono le seguenti proprietà:

1
2
3
4
5

Detto questo, niente farebbe pensare che i vettori siano entità che possono tranquillamente descrivere delle realtà economiche. Consideriamo la seguente tabella:

	gennaio	Febbraio	Totale
Prodotto A	10	11	21
Prodotto B	20	19	39

restituisce le vendite in kg di due prodotti in un negozio nei primi due mesi dell'anno. Supponiamo che entrambi i prezzi p₁ e p₂ del prodotto A e del prodotto B praticati nel mese di gennaio vengano aumentati in febbraio del 5%.
Rappresentiamo con i vettori:
1 le vendite di gennaio;
2 le vendite di febbraio;
3 la vendita totale;
4 i prezzi di gennaio;
5 i prezzi di febbraio.

I vettori richiesti sono

                        vettore delle vendite di gennaio
                       vettore delle vendite di febbraio
    vettore delle vendite totali
                      vettore dei prezzi a gennaio

I prezzi di febbraio sono incrementati del 5% rispetto ad i prezzi di gennaio; dunque essi valgono

dunque

vettore dei prezzi a febbraio.

Un altro esempio può essere il seguente.
Un'azienda che opera in due mercati distinti, distribuisce i prodotti 1 e 2.
Le quantità vendute in quintali di ciascun prodotto in una settimana sul mercato A e sul mercato B sono date nella seguente tabella.

	A	B
1	100	160
2	120	180

A seguito di una campagna pubblicitaria si ritiene possibile incrementare le vendite nel mercato A del 10% e nel mercato B del 20%. Trova
a i vettori relativi alle quantità vendute nei due mercati prima della campagna pubblicitaria;
b il vettore che indica le vendite complessive prima della campagna pubblicitaria;
c i vettori richiesti nei due punti precedenti dopo la campagna pubblicitaria.

Per il punto a avremo

Per il punto b avremo

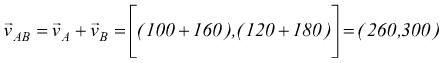
per trovare il punto c dobbiamo incrementare il vettore del mercato 1 per un fattore di scala pari a 0,1 (10%) ed incrementare il vettore di un fattore di scala pari a 0,2 (20%).

la nuova tabella delle vendite appare come segue:

	A	B
1	110	192
2	132	216

Il motore di calcolo di Excel può automatizzare in modo opportuno le operazioni effettuate. Nel file matrici.xls foglio 1 la matrice delle vendite viene indicata nella barra dei nomi con identificatore inserito nella barra dei nomi mat1.

Per incrementare il mercato A del 10% (0,1) e il mercato B del 20% (0,2) può essere usata una matrice diagonale che ha identificatore nella barra dei nomi mat2.

ci posizioniamo in cella A4 ed introduciamo la formula
=MATR.PRODOTTO(mat1;mat2)

poi selezioniamo l'intervallo A4:B5, facciamo clic nella barra della formula assicurandoci che il cursore lampeggiante sia in essa e battiamo CTRL+MAIUSC+INVIO. Il risultato ci permette di ottenere la matrice degli incrementi:

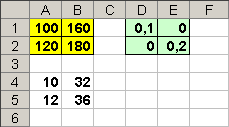
successivamente, in cella A7 inseriamo la formula
=A1+A4

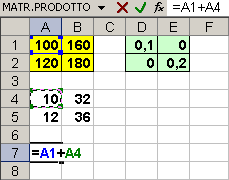
trasciniamo oppure facciamo il copia/incolla da A7 a B8, ottenendo il seguente risultato che ci restituisce la situazione delle vendite dopo un incremento del 10% del mercato A e del 20% del mercato B.

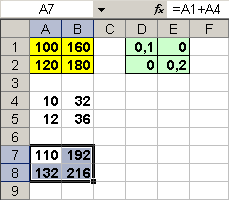
Come si vede è facile e dilettevole eseguire delle operazioni sulle matrici con Excel.

Per semplicità, predisponiamo sul Foglio2 una coppia di matrici 3x3. La prima matrice viene identificata nella barra dei nomi con la lettera A.

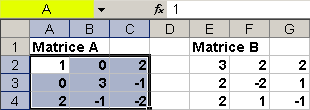
La seconda matrice ha identificatore B nella barra dei nomi.

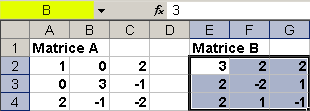
In cella A7 introduciamo la formula
=MATR.INVERSA(A)

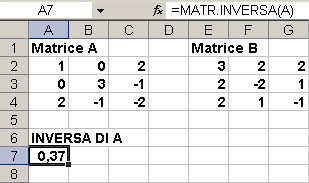
dopo aver selezionato l'intervallo A7:C9 facciamo clic per entrare nella barra della formula e poi battiamo CTRL+MAIUSC+INVIO.

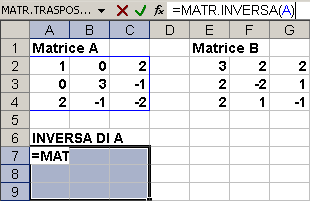
Il risultato ottenuto sarà, appunto, la rappresentazione della matrice inversa della matrice A.

La somma delle due matrici può essere eseguito come nel caso precedente. In cella E7 viene introdotta la formula: =A2+E2 .

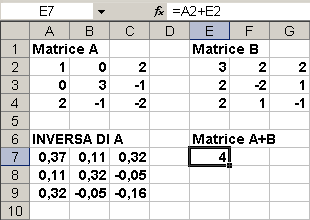
poi trasciniamo o eseguiamo il copia/incolla sull'intervallo E7:G9. Otteniamo la somma delle due matrici A e B.

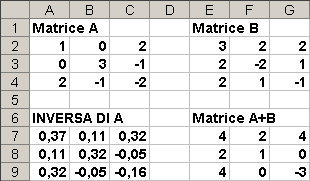
Anche il prodotto tra le due matrici A e B può essere ottenuto col metodo precedentemente visto. In cella A12 introduciamo la formula
=MATR.PRODOTTO(A;B)

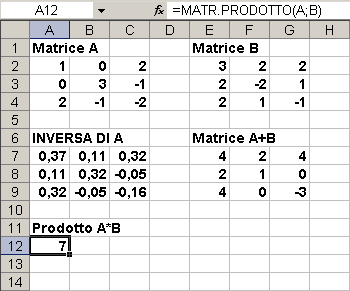
poi come già visto in precedenza è sufficiente selezionare l'intervallo A12:C14, fare clic nella barra dei nomi e battere CTRL+MAIUSC+INVIO. Nell'immagine seguente si nota il risultato del prodotto tra le due matrici A e B come una ulteriore matrice 3x3.

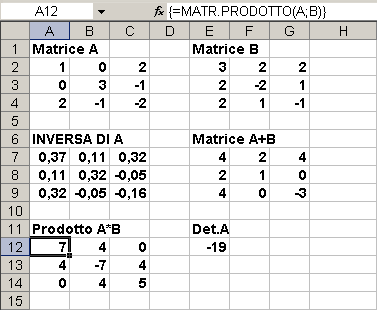
Si vede, inoltre, come in cella E12 sia stato calcolato il determinante della matrice A, introducendo in quella cella la formula:
=MATR.DETERM(A)

Sono numerose le funzioni che possono operare sulle matrici, qui di seguito un breve elenco con descizione.

Funzione	Descrizione
CERCA.X()	Cerca un valore in una matrice in base a una modalità di confronto e restituisce la matrice trovata.
DATI.ORDINA()	Ordina una matrice per righe o colonne in base a un indice definito da una colonna o una matrice.
DATI.ORDINA.PER()	Ordina una matrice in base ai valori di un'altra matrice.
FILTRO()	Filtra un intervallo di dati in base a criteri molteplici.
INDICE()	Restituisce un valore o una matrice selezionata in base a indici di riga e colonna.
MATR.CASUALE()	Crea una matrice di qualsiasi numero di righe e colonne composta da numeri casuali compresi in un intervallo fissato.
MATR.INVERSA()	Restituisce la matrice inversa della matrice di partenza.
MATR.PRODOTTO()	Restituisce il prodotto di due matrici.
MATR.SOMMA. PRODOTTO()	Moltiplica elemento per elemento due matrici e ne somma i risultati.
MATR.TRASPOSTA()	Calcola la trasposta di una matrice, ovvero la matrice ottenuta invertendo le righe con le colonne (da una matrice 2 × 3 si passa a una 3 × 2).
MATR.UNIT()	Restituisce una matrice unitaria di qualsiasi dimensione (tutti gli elementi pari a 0 tranne quelli sulla diagonale principale pari a 1).
MATRICE.A.TESTO()	Restituisce il contenuto della matrice, qualunque esso sia, come testo.
SCARTO()	Restituisce una matrice estratta da una precedente, in una posizione definita.
SEQUENZA()	Crea una sequenza di numeri secondo i parametri impostati.
UNICI()	Estrae tutti gli elementi unici da una matrice data.
VALORE.A.TESTO()	Restituisce il contenuto di un'area come testo.

Come si vede alcune di loro non iniziano nemmeno coi prefisssi MATR. o MATRICE.