Resistore
I resistori sono dispositivi che hanno la proprietà di opporsi alla circolazione della corrente elettrica e di degradare in calore l'energia elettrica assorbita. Un resistore si presenta come un dispositivo provvisto di due morsetti; il suo comportamento elettrico, in corrente continua, soddisfa la legge di Ohm:
I resistori chiamati anche, in gergo tecnico, resistenze sono sono componenti elettrici il cui funzionamento è strettamente legato alla nozione di corrente elettrica.
Corrente elettrica
La corrente elettrica che percorre un conduttore viene spesso descritta come un flusso di cariche elettriche che percorre il conduttore stesso. Questa interpretazione è piuttosto generica, nel senso che, in un qualsiasi conduttore elettrico, a temperatura ambiente, sono sempre presenti degli elettroni liberi che si muovono, in maniera casuale, in molteplici sensi, alla velocità dell'ordine di 106 m/s senza dare luogo ad alcun effettivo trasferimento organizzato di cariche elettriche in una data direzione.
Se dovessimo intersecare il conduttore con un piano immaginario, il trasporto di netto carica elettrica attraverso tale sezione sarebbe nullo.
Ma se si connettono gli estremi del conduttore, come ad es. un filo di rame ad una batteria elettrica, avremo un trasporto netto di carica non nullo, tale da dar luogo ad una corrente elettrica.
Per avere una corrente elettrica è necessario, dunque, disporre di un campo elettrico applicato ad un conduttore. Infatti, se avessimo una spira chiusa, ad esempio di rame, essa si troverebbe in equilibrio elettrostatico e in essa non sarebbe possibile rilevare alcun passaggio di corrente elettrica.
Aggiungendo un generatore elettrico (o batteria) si impone una differenza di potenziale tra i capi della spira connessa, questa differenza di potenziale permette l'instaurarsi di un campo elettrico all'interno della spira ed il campo provoca il moto di cariche lungo la spira stessa.
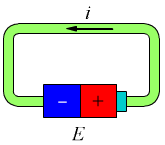
Questo movimento di cariche viene indicato col simbolo i ed esprime la quantità di carica elettrica che passa attraverso una qualsiasi sezione della spira nell'unità di tempo. In termini incrementali avremo:
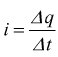che
in termini differenziali si scrive
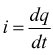
da cui è possibile ottenere la quantità di carica transitante riferita ad un generico intervallo di tempo:
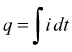
dove dq è la quantità di carica (positiva) che passa in un tempo dt attraverso un piano immaginario che taglia trasversalmente il conduttore. Il verso della corrente elettrica è quello nel quale si muovono i portatori di carica positivi. L'unità del sistema SI per la corrente elettrica è l'ampere (A): 1 A = 1 C/s.
Densità di corrente
La densità di corrente è una quantità vettoriale orientata nella stessa
direzione in cui viaggiano le cariche positive in moto. Per ciascun elemento
di area della sezione l'intensità J è pari alla corrente che lo attraversa
per unità di area Si può indicare la corrente attraverso l'elemento di superficie
come 
dove dS è il vettore relativo
a quell'elemento di area ed è perpendicolare ad esso.
La corrente totale attraverso la superficie è allora
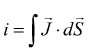
Se la corrente e uniforme su tutta la superficie e parallela a dS, allora
è costante e parallela al
vettore 
e l'equazione precedente
diventa
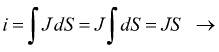
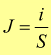
dalle due eq. precedenti si deduce che l'unita di misura SI per la densita di corrente è l'ampere sul metro quadrato (A/m2). Il disegno seguente suggerisce come possa variare la densità di corrente lungo uno stesso conduttore.
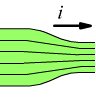
Le linee di flusso rappresentano la densità di corrente attraverso il conduttore. La corrente, diretta verso destra, subisce un passaggio da una sezione più larga a sinistra ad una più stretta a destra. In questo passaggio la carica si conserva, nel trasferimento la quantità di carica, e quindi l'intensità di corrente, non possono variare. La densità di corrente però cambia, ed e maggiore nel conduttore più stretto. La spaziatura tra le linee flusso suggerisce qualitativamente questo incremento della densità di corrente: a più linee assiepate corrisponde una maggiore densità di corrente.
Resistenza e resistività elettrica
Se si applica la stessa differenza di potenziale tra le estremità di un filo di rame e di ottone geometricamente simili, ne risultano correnti assai diverse. La caratteristica del conduttore che entra in gioco in questo caso è la sua resistenza elettrica.
Per definizione, la resistenza elettrica esprime la difficoltà che incontra la corrente elettrica a fluire all'interno di un conduttore.
La resistenza di un conduttore tra due punti si determina applicando una differenza di potenziale V tra quei punti e misurando la corrente i che si stabilisce. La resistenza R è data da
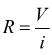
L'unita del sistema SI per la resistenza, come definita nell'ultima equazione , è il volt su ampere. Quest'unita di misura è denominata, ohm (simbolo Ω ). Cioe 1Ω=1V/A. Negli schemi elettrici una resistenza è rappresentata dal seguente simbolo
se riscriviamo l'eq. precedente come 
notiamo come per una data differenza di potenziale, più è grande la resistenza
che si oppone al fluire delle cariche, più risulta piccola la corrente.
La resistenza di un conduttore dipende dalle caratteristiche geometriche
e dal materiale da cui è costituito quest'ultimo.
Si verifica sperimentalmente che
● La resistenza elettrica di un conduttore
è direttamente proporzionale alla lunghezza quest'ultimo.
● La resistenza elettrica di un conduttore
è inversamente proporzionale alla sezione di quest'ultimo.
Un parametro che tiene conto di tutte queste circostanze è la resistività ρ del materiale, definita come il rapporto tra il campo elettrico e la densità di corrente.
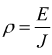
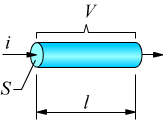
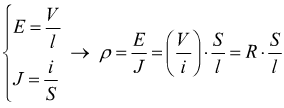quindi
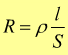
Da quest'ultima formula si deduce che la resistività coincide con la resistenza
elettrica che un campione di materiale di 1cm di lunghezza e di 1cm2
di sezione oppone al passaggio di corrente elettrica la sua unità di misura
è l'Ω·m.
La seguente tabella mostra come la resistività sia un parametro strettamente
legato alla natura fisico-chimica del materiale; i dati sono riferiti ad
una temperatura ambiente di 293 K.
| Materiale | Resistività ρ (Ω·m) | Coefficiente termico α(K-1) |
| Argento | 1,62×10-8 | 4,1×10-3 |
| Rame | 1,69×10-8 | 4,3×10-3 |
| Oro | 2,35×10-8 | 4,0×10-3 |
| Alluminio | 2,75×10-8 | 4,4×10-3 |
| Manganina | 4,82×10-8 | 0,002×10-3 |
| Tungsteno | 5,25×10-8 | 4,5×10-3 |
| Ferro | 9,68×10-8 | 6,5×10-3 |
| Platino | 10,6×10-8 | 3,9×10-3 |
| Silicio | 2,5×10-8 | -70×10-3 |
| Nichel | 7×10-8 | 5,9×10-3 |
| Ottone | 3,9×10-8 | 2×10-3 |
| Acciaio | 11×10-8 | 5×10-3 |
| Costantana | 49×10-8 | 0,01×10-3 |
| Acciaio inox | 70×10-8 | 1×10-3 |
| Tantalio | 13×10-8 | 3,1×10-3 |
| Piombo | 22×10-8 | 3,9×10-3 |
| Vetro | 1010÷1014 | |
| Gomma | ∼1013 |
Spesso si parla di conducibilità elettrica σ di un materiale; essa è semplicemente il reciproco della resistività:
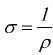
che nel SI viene quantificata dimensionalmente in siemens su metro [S/m]. Ricordiamo che 1S=1/Ω.
I valori delle principali proprietà fisiche variano al modificarsi della temperatura: la resistivita non fa eccezione. La relazione tra la temperatura e la resistività per la maggior parte dei metalli, è sostanzialmente, tanto che per la maggior parte degli scopi tecnici si assume:
Dove To è una temperatura di riferimento opportunamente scelta e ρo a la resistività a quella temperatura. Spesso si assegna To = 293 K (temperatura ambiente), per la quale ρo = 1,69 10-8 Ω·m per il rame.
Poiché la temperatura compare nell'equazione precedente solo come differenza, non importa se si usa la scala Celsius o la scala Kelvin in tale equazione, in quanto l'unita di intervallo di temperatura di queste scale è identica. La quantità α è chiamata coefficiente termico di resistività.
La formula precedente può essere riscritta come
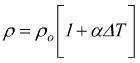
moltiplicando entambi i membri per l/S :
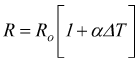
che equivale a scrivere
