Premessa
Sappiamo che in un circuito costituito da un' unica maglia contenente una resistenza R ed un condensatore C la tensione la tensione ai capi del condensatore non raggiunge immediatamente il valore finale di equilibrio Vc=E (pos.1)ma vi tende con andamento esponenziale crescente con legge:
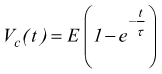
la rapidità con cui Vc tende ad al valore del generatore E viene determinato dalla costante di tempo τ=R·C.
Se nello stesso circuito la batteria E viene rimossa (cortocircuitata: pos.2) improvvisamente, la tensione (e quindi la carica ricordando che Q=C·V) non si annulla all'istante ma tende a zero in modo esponenziale.
con Vo il valore a cui era inizialmente carico C.
Carica dell'induttore
Un fenomeno analogo (duale) avviene se si introduce o si rimuove improvvisamente una forza elettromotrice (f.e.m.) continua E in un circuito costituito da una sola maglia contenente un'induttanza L ed una resistenza R.
Quando l'interruttore T chiude il circuito passando dalla pos.0 alla pos.1 la corrente attraversa la resistenza e se non ci fosse l'induttanza la corrente raggiungerebbe istantaneamente il valore E/R.
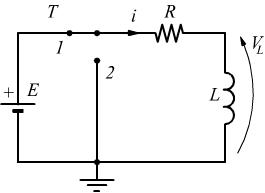
A causa dell'induttanza, nel circuito compare una f.e.m. indotta VL.
Per la legge di Lenz, questa f.e.m. si
oppone alla crescita della corrente (VL ha polarità opposta rispetto
la batteria E).
La resistenza, dunque, risponde alla differenza delle due f.e.m. : una costante
E della batteria e l'altra variabile VL. Sappiamo che
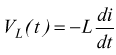dovuta
all'autoinduzione.
Finché è presente questa seconda f.e.m. la corrente circolante è minore di E/R.
Inizialmente l'induttanza si comporta in modo da contrastare la variazione di corrente. Dopo un certo tempo l'induttanza si comporta come un normale filo conduttore. Facendo l'equazione alla maglia si ha
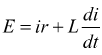
questa è un'equazione differenziale nella variabile i(t) e nella sua derivata prima di/dt. Bisogna,allora, trovare la funzione i(t) che soddisfa questa equazione con la condizione iniziale i(0)=0. La soluzione di questa risulta essere
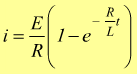ponendo
[
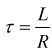s ] avremo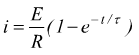 
La corrente nel circuito avrà andamento esponenzialmente crescente tendente al valore di equilibrio E/R.
Scarica dell'induttore
Se l'interruttore T viene portato in pos.2 l'effetto è quello che di staccare (cortocircuitare) la batteria dal circuito.
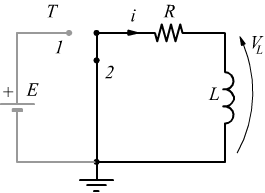
In assenza della batteria, la corrente nel circuito deve diminuire, essa, però, non può cadere istantaneamente a zero, deve giungervi gradualmente in un certo tempo. L'equazione differenziale che regola questa diminuzione è
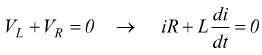
La soluzione di questa equazione differenziale con la condizione iniziale i(0)=E/R è
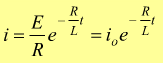
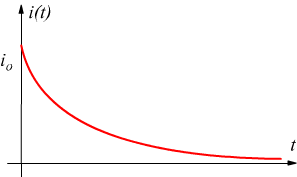
Sia la corrente in aumento che quella in diminuzione in un circuito RL sono regolate dalla stessa costante di tempo induttiva τ=L/R.
Più in generale per i circuiti RL può essere usata la seguente formula
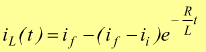
ii : corrente iniziale nell'induttanza
ic : corrente finale nell'induttanza se la consideriamo un corto
circuito come accadrebbe per t → ∞.
Dalle formule si intuisce come l'induttore, durante un transitorio di accensione, possa essere considerato un circuito aperto per t=0 ed un corto circuito per t → ∞.