Accoppiamenti dei circuiti

      

Due circuiti si dicono accoppiati quando l'energia elettrica può passare da un circuito all'altro.
Nel disegno seguente è riportato lo schema a blocchi di un accoppiamento tra un circuito generatore ed uno utilizzatore.

1. Diretto: il circuito di accoppiamento contiene esclusivamente elementi resistivi.
2. Capacitivo: il circuito di accoppiamento contiene delle capacità. Tale tecnica è utilizzata nel collegamento in cascata di più amplificatori.
3. Induttivo: l'Accoppiamento è realizzato mediante induttanze o sfruttando il fenomeno della mutua induzione magnetica.

In alcuni casi, il requisito fondamentale dell'accoppiamento è quello di realizzare il massimo trasferimento di energia tra generatore e carico.
Il circuito seguente rappresenta il più semplice accoppiamento tra generatore e utilizzatore.

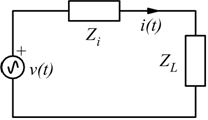
Valutando le condizioni per il massimo trasferimento di energia.
Supponendo che le impedenze Z_i e Z_L siano del tipo:

La potenza attiva assorbita dal carico Z_L vale:   La corrente i è, per la legge di Ohm:

Dove v ed i sono i valori efficaci della tensione e della corrente. Sostituendo la precedente relazione, si ha:

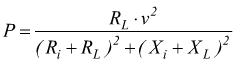
Le condizioni di massimo trasferimento di energia si ricava ponendo uguale a zero la derivata rispetto a R_L della formula precedente si ottiene:

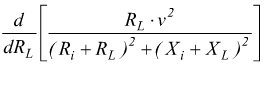
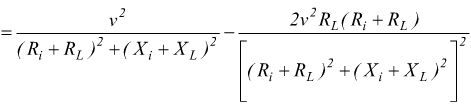
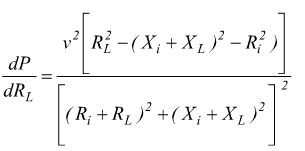
essa si annulla per         

Le precedenti uguaglianze rappresentano le condizioni per il massimo trasferimento di energia.

Come si nota, si ha il massimo trasferimento di potenza quando la Z_L è impedenza immagine della Z_i (uguale parte reale e parte immaginaria opposta).

Se queste condizioni non sono soddisfatte è necessario interporre tra generatore ed utilizzatore un apposito circuito denominato adattatore di impedenza.
Nella seguente figura si mostra uno dei più semplici circuiti adattatori di impedenza noto come partitore resistivo.

Affinché si realizzi l'adattamento di impedenza devono verificarsi contemporaneamente le seguenti condizioni:

Risolvendo il precedente sistema si ricavano i valori della resistenza del partitore:

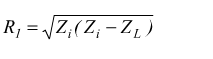
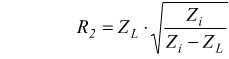
Accoppiamento per mutua induzione

    

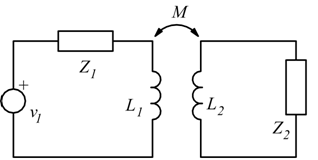
Nel disegno seguente è riportato il sistema elettrico di un accoppiamento realizzato per mutua induzione tra due circuiti denominati primario e secondario. Questo accoppiamento è usato in radioelettronica per la realizzazione di circuiti trasmettitori e ricevitori radio.

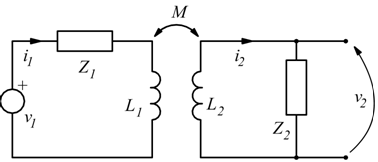
Le impedenze Z₁ e Z₂ sono quelle complessive del primario e del secondario ed in esse si intende conglobato il valore delle induttanze L₁ ed L₂.
Per la legge dell'induzione elettromagnetica se nel primario circola una corrente sinusoidale,nel secondario nasce una forza elettromotrice (f.e.m.) indotta.
Se il secondario è chiuso su un carico Z₂ in esso si manifesta una corrente i₂ che a sua volta agisce per mutua induzione sul primario facendo nascere una nuova f.e.m. che si combina con quella del generatore.
Queste mutue interazioni sono regolate dalle seguenti equazioni:

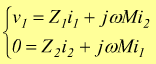
Nella prima formula    tiene conto dell'effetto del secondario sul primario, viceversa per il termine  nella seconda equazione. Il coefficiente di mutua induzione M è legato alle induttanze L₁ ed L₂ dalla relazione:

Il parametro k è il coefficiente di accoppiamento compreso tra 0 e 1. Per k=1 si ha il massimo accoppiamento che si ottiene quando tutte le linee di flusso magnetico dell'avvolgimento primario si concatenano con quello secondario.
Per facilitare lo studio dei circuiti accoppiati si effettua un riporto del secondario al primario oppure un riporto del primario al secondario.
Se si ricava i₂ dalla seconda equazione e si sostituisce nella prima si ottiene

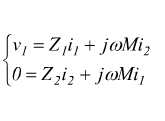
quindi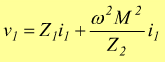        

La precedente relazione mostra che per ciò che riguarda il primario è come se il secondario non esistesse purché nel primario si riporti una impedenza:

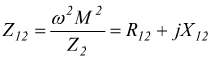
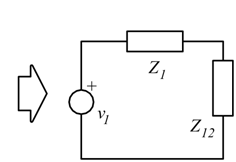
Supponendo     si ha:

Analogamente se dalla formula  si ricava i₁ e si sostituisce nella   si ha:

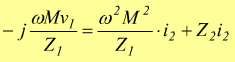
La precedente relazione mostra che il primario si può trasferire al secondario riportando una f.e.m. v₂₁ e una impedenza Z₂₁ pari:

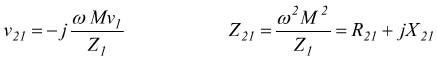
Supponendo   si ha:

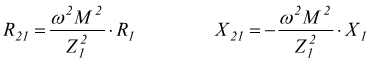
Di seguito è illustrato il circuito equivalente con riporto al secondario.

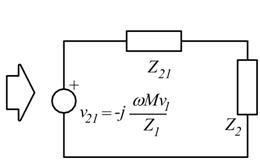
Questo schema è del tutto equivalente al precedente e pertanto le condizioni per il massimo trasferimento di energia tra primario e secondario, sono:

La precedente relazione si può verificare se le reattanze del primario e del secondario sono dello stesso tipo oppure se i due circuiti sono in risonanza per cui la parte reattiva X₁ e X₁₂ è nulla.

Si ha dunque, il massimo trasferimento di potenza dal primario al secondario quando la Z₁₂ è impedenza immagine della Z₁ (uguale parte reale e parte immaginaria opposta). In tal caso anche la Z₂₁ risulterà essere impedenza immagine di Z₂.

Un caso particolare è quello in cui le bobine sono accoppiate tramite un nucleo di materiale ferromagnetico (in bassa frequenza) in tali condizioni si può ritenere k=1 come nel caso del trasformatore di adattamento in figura, dove m è il rapporto fra le spire.

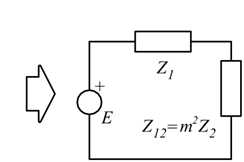
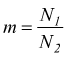
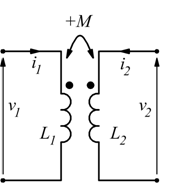
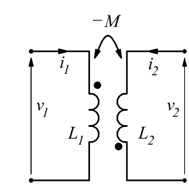
Per questi tipi di circuiti è utile ricordare la regola dei punti: M è positivo se i due punti sono affiancati, al contrario è negativo se non sono affiancati.

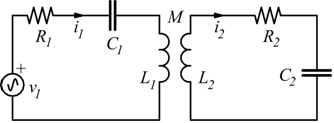
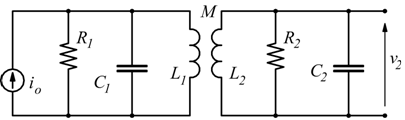
Circuiti risonanti accoppiati (Filtri di banda)

    

Di seguito si mostrano gli schemi elettrici di due circuiti risonanti accoppiati per mutua induzione. Questo è il  circuito risonante serie .

Il seguente è il  circuito risonante parallelo  .

Si suppone che entrambi i circuiti siano accordati sulla stessa frequenza di risonanza:

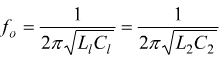
L'analisi dei due circuiti è fra loro formalmente identica solo che nel tipo serie si fa riferimento alle correnti del primario e secondario, nel tipo parallelo si fa riferimento alle tensioni.
La risposta in frequenza delle correnti o delle tensioni dipende fortemente dal grado di accoppiamento tra i due circuiti come mostrato in figura seguente.

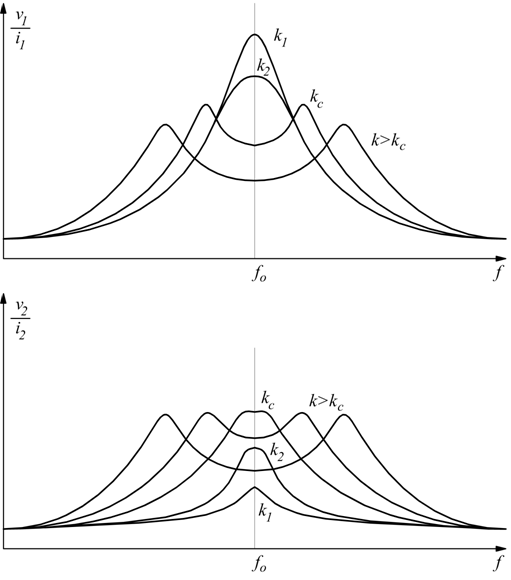
Se il coefficiente di accoppiamento k è piccolo (accopiamento lasco) le curve di risposta del primario e del secondario sono come quelle di due circuiti risonanti indipendenti.
All'aumentare del grado di accoppiamento la risposta del primario e del secondario diviene più ampia e il picco più smussato.
Quando si raggiunge il cosiddetto accoppiamento critico k_c la corrente e la tensione al secondario raggiungono il massimo valore e la curva di risposta è molto appiattita.
Per questo motivo il circuito è detto filtro di banda. In tali condizioni si ha il massimo trasferimento di energia e si può dimostrare che valgono le seguenti relazioni:

Circuito serie:

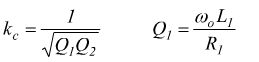
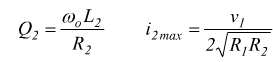
Circuito parallelo:

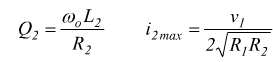
Con Q₁ e Q₂ coefficienti di risonanza del primario e del secondario considerati separatamente.

Il circuito è utilizzato in alta frequenza come filtro passa-banda poiché per k=k_c la risposta è piatta entro la banda B:

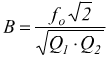
Per frequenze esterne a tale banda il segnale di uscita è fortemente attenuato grazie alla elevata selettività del circuito.