Condensatore
Il condensatore è un componente elettrico, in grado di accumulare e conservare energia elettrica, costituito da due conduttori disposti in modo tale che quando su uno di essi si trova una carica elettrica +Q l’altro acquisisca per induzione la carica –Q.
In virtù del teorema di Gauss sul campo elettrico è’ possibile dimostrare che il campo elettrico di una distribuzione piana di cariche è
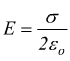
dove σ è la densità di carica sull’unità di superficie ed εo
è la costante dielettrica del vuoto di valore εo=8,85·10-12
F/m (oppure, indifferentemente misurabile in C2/Nm2).
Il vettore campo elettrico per una carica positiva piana, deve essere disegnato
come uscente dalla superficie.
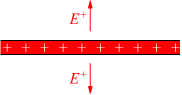
Se la carica fosse negativa, per convenzione, il vettore campo avrebbe avuto la direzione diretta verso la superficie. Se si avvicinano in modo parallelo, due lamine piane, cariche di segno opposto della stessa densità di carica, si ottiene una la seguente configurazione:
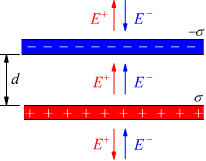
Come si vede rappresentato, i due vettori campo E+ ed E- sono uguali ed opposti: essi si elidono nello spazio esterno alle lamine metalliche e si sommano nello spazio tra i due piani di carica, dando luogo ad un campo risultante.
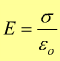
Il sistema descritto è un condensatore e le lamine utilizzate vengono denominate armature.
Capacità di un condensatore piano
La capacità elettrostatica di un conduttore viene definita come
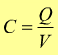 [
F ] Farad
[
F ] Farad
esso è il rapporto tra la carica che si trova sul conduttore e il suo potenziale.
Nel caso del condensatore piano appena descritto, la differenza di potenziale ai suoi capi è
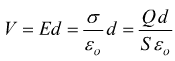
dove Q è la carica accumulata su una delle due superfici di valore S mentre d è la distanza tra le armature, cioè tra le due pareti del condensatore.
La capacità di un condensatore risulta così essere:
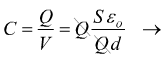
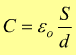
Si vede come quest'ultima possa essere utilizzata per aumentare la capacità del condensatore, essa è infatti, correlata col materiale che si trova tra le armature.
Come si è visto, l'unità di misura della capacità di un condensatore è il Farad [F]. In base alla definizione data questa unità di misura corrisponde ad 1 coulomb su volt:
1 farad=1 F=1 coulomb/volt= 1 C/V
Il farad è una unità di misura molto grande per la maggior parte degli
impieghi pratici. I sottomultipli del farad come il microfarad, il nanofarad
ed il picofarad sono unità più adatte :
1 microfarad= 1 μF=10-6 F
1 nanofarad= 1 nF=10-9 F
1 picofarad= 1 pF=10-12 F
La presenza della superficie S nella formula della capacità di un condensatore suggerisce come questa grandezza sia strettamente correlata con la geometria del conduttore considerato.
Dielettrico
Se riempiamo lo spazio tra le armature di un condensatore con un dielettrico,
che è un materiale isolante come olio minerale o plastica, le proprietà
fisiche del sistema cambiano. Questo vale in generale quando siamo in presenza
di due conduttori con carica opposta separati da una distanza r. Ripetendo
in tal caso l'esperienza di Coulomb si ottiene la stessa legge che si ha
nel vuoto, salvo un diverso valore della costante di proporzionalità. più
precisamente si trova che la forza ![]() che
si esercita tra le due cariche q e q' poste alla distanza r tra loro vale
:
che
si esercita tra le due cariche q e q' poste alla distanza r tra loro vale
:
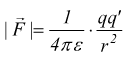
La costante ε è detta costante dielettrica del materiale isolante
considerato e vale:
ε=εo·εr
εo=costante dielettrica del vuoto
εr è invece un numero puro sempre maggiore di 1 chiamato
costante dielettrica relativa.
Nel caso del condensatore si possono avere solo due casi
1 lo spazio tra le armature è vuoto;
2 lo spazio è riempito uniformemente con un
dielettrico omogeneo.
In questo secondo caso, il campo elettrico ![]() ed il corrispondente potenziale elettrostatico V sono in ogni punto εr
volte più piccoli delle corrispondenti grandezze nel vuoto.
ed il corrispondente potenziale elettrostatico V sono in ogni punto εr
volte più piccoli delle corrispondenti grandezze nel vuoto.

L'introduzione di un dielettrico ha come effetto quello di limitare il
potenziale differenza che può essere applicata tra le piastre ad un certo
valore Vmax, chiamato potenziale di rottura.
Se questo valore viene sostanzialmente superato, il dielettrico il materiale
si romperà e formerà un percorso conduttivo tra le piastre.
Ogni materiale dielettrico ha una rigidità dielettrica
caratteristica, che è il massimo valore del campo elettrico sopportabile.
Nella seguente tabella sono riportati i valori della costante dielettrica
relativa per alcuni significativi materiali.
| Materiale | Costante dielettrica relativa er | rigidità dielettrica (kV/mm) |
| Aria (1bar) | 1,00054 | 3 |
| Teflon | 2,1 | 20 |
| Polistirene | 2,6 | 24 |
| Legno (oak) | 3,3 | 4 |
| Carta | 3,5 | 16 |
| Olio industriale | 4,5 | 35 |
| Vetro (pyrex) | 4,7 | 14 |
| Mica | 5,4 | 118 |
| Porcellana | 6,5 | 14 |
| Marmo | 8,3 | 9 |
| Silicio | 12 | 4 |
| Germanio | 16 | 12 |
| Etanolo | 25 | 13 |
| Acqua (25°C) | 78,5 | 81 |
| Acqua (20°C) | 80,4 |
Come si vede a parità di cariche elettriche la presenza del dielettrico determina un abbassamento del valore sia del campo elettrico che del potenziale nel rapporto costante 1/εr ma in tal caso cambia anche il valore della capacità precedentemente trovato in:
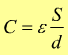
Cioè il valore della capacità può essere vantaggiosamente aumentato del fattore costante εr cioè: C=εr·Co.
Calcolo della carica e del potenziale
La quantità di carica Q accumulata su ciascuna delle armature del condensatore può essere calcolata tramite la legge di Gauss.
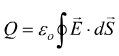
Se consideriamo i casi in cui il flusso che attraversa la superficie E
ha modulo costante con i vettori ![]() e
e ![]() paralleli
tra loro, si otterrebbe come caso particolare
paralleli
tra loro, si otterrebbe come caso particolare
![]()
La differenza di potenziale V tra le due armature è legata al campo elettrico E dall'equazione:
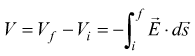
dove ds è il differenziale di un qualunque percorso che va da un'armatura
all'altra. Si sceglierà sempre un cammino che va dal piatto negativo a quello
positivo, in tale cammino i vettori ![]() e
e ![]() hanno la stessa
direzione e verso opposto in tal modo il prodotto scalare
hanno la stessa
direzione e verso opposto in tal modo il prodotto scalare ![]() sarà
uguale a
sarà
uguale a ![]() ed il
secondo membro dell'equazione sarà sempre positivo.
ed il
secondo membro dell'equazione sarà sempre positivo.
Condensatore piano
Se prendiamo in considerazione un condensatore piano come rappresentato nel seguente schema
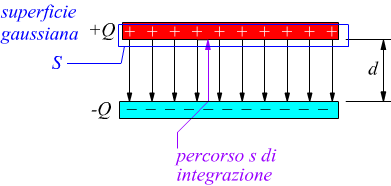
ipotizzando una superficie gaussiana che racchiuda tutta la carica Q del piatto positivo avremo:
![]()
come già visto prima; inoltre per la differenza di potenziale il secondo integrale avrà valore
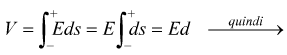
![]()
essendo Q=CV, sostituendo si avrebbe
![]()
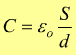
dove si riconosce come la capacità dipende esclusivamente da fattori geometrici.
Condensatore cilindrico
Il seguente schema mostra un condensatore cilindrico di lunghezza L visto
in sezione costituito da due cilindri coassiali di raggi a e b.
Ogni armatura contiene una carica Q.
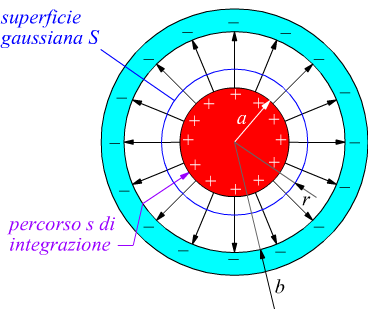
Come superficie gaussiana scegliamo un cilindro di raggio r e lunghezza L coassiale alle due armature collocato come nel disegno. Per la carica immagazzinata avremo:
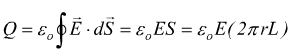 per
cui
per
cui
![]()
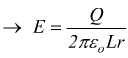
per la differenza di potenziale tra le due armature sostituendo con ds= – dr:
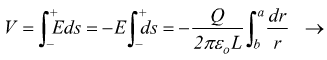
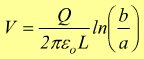
dalla relazione Q=CV otteniamo poi
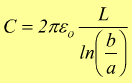
Condensatore sferico
Lo schema precedente può anche rappresentare la sezione longitudinale (o
indifferentemente trasversale) di un condensatore sferico, costituito da
due gusci sferici concentrici di raggi a e b.
La superficie gaussiana può essere ccostituita in questo caso da una sfera
di raggio r, concentrica ai due elementi precedenti.
Per la carica elettrica, otteniamo anche in questo caso:
![]()
![]()
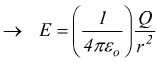
eseguendo il calcolo per la differenza di potenziale, sostituendo sempre con ds= - dr:
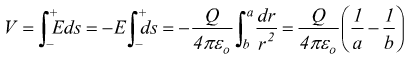
ottenendo
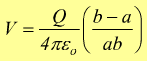
ricordandoci della relazione Q=CV, la capacità di un condensatore sferico può esprimersi come:
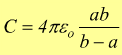
Energia immagazzinata in un condensatore
Dallo studio sul campo elettrico sappiamo che la relazione che lega tra
loro energia potenziale del campo con la carica elettrica e la differenza
di potenziale è U=qV.
Ipotizziamo che una carica q venga trasferita tra le due armature scariche.
La differenza di potenziale V tra i due piatti diventerà q/C, se poi si
trasporta una ulteriore carica dq l'incremento di lavoro richiesto sarà
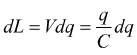
Notiamo come questa scrittura sia coerente con la definizione di energia
potenziale associata ad un campo elettrico U=qV.
Il lavoro necessario per portare la carica totale del condensatore al valore
finale Q sarà :
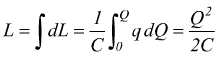
questo lavoro viene immagazzinato come energia potenziale elettrica. Dunque:
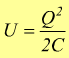 essendo
Q=CV
essendo
Q=CV
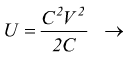
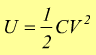
Forza esercitata tra le armature di un condensatore
Per il principio di conservazione dell'energia in un campo conservativo avremo
![]()
per un moto unidimensionale
![]()
in termini differenziali
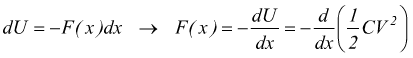
quindi
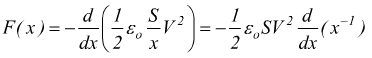
si ottiene
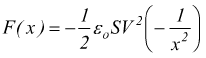
per x=d distanza tra i piatti del condensatore
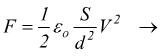
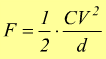
essendo Q=CV
 edutecnica
edutecnica