Principio di conservazione dell’energia
L'energia meccanica Emec di un sistema viene definita come la somma dell'energia potenziale U e dell'energia cinetica K relativa ai corpi che lo compongono
![]()
la conservazione dell'energia meccanica riveste particolare importanza quando entro il sistema agiscono solo forze conservative.
Dobbiamo partire dall'ipotesi che il sistema sia isolato dall'ambiente esterno; vale a dire che non vi sia possibilità che le forze esterne al sistema modifichino l'energia interna del sistema, cioè che non possano esserci dei trasferimenti di energia tra il sistema e l'esterno.
Quando una forza conservativa compie il lavoro L su un corpo all'interno di un sistema isolato, essa, trasferisce energia tra l'energia cinetica K del corpo e l'energia potenziale U del sistema. Variazione di energia cinetica ΔK vale:
![]()
Mentre la variazione dell'energia potenziale ΔU su un corpo può essere definita come l'opposto del lavoro svolto sul corpo stesso dalla forza conservativa del sistema agente sul corpo
![]()
il caso tipico a cui abbiamo fatto riferimento più volte e quello del lancio in verticale di una massa rispetto ad un piano di riferimento in presenza del campo gravitazionale.
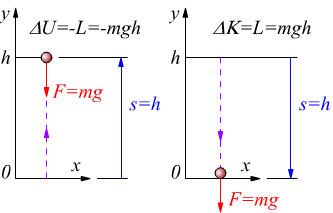
Dagli schemi, si vede che il lavoro compiuto dal campo durante la fase di sollevamento del grave è negativo mentre quando questo percorre la traiettoria opposta è positivo.
Basandoci su queste considerazioni, indicando con (1) e (2) due differenti istanti del moto di un corpo
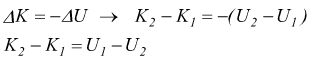
Il principio di conservazione dell'energia, consiste nella formula:
![]()
La somma dell'energia cinetica e potenziale in qualunque stato di un sistema è uguale alla somma di energia cinetica e potenziale per un qualsiasi altro stato del sistema.
Questo sotto l'ipotesi che il sistema sia isolato e che sui corpi agiscano solo forze conservative.
Quando in un sistema isolato agiscono solo forze conservative, l'energia cinetica e l'energia potenziale prese singolarmente possono variare, ma la loro somma costituita dall'energia meccanica Emec del sistema non cambia.
Infatti dalla precedente relazione si deduce che
![]()
cioè si conserva l'energia meccanica.
Energia meccanica e attrito
Nello schema si vede un blocco di massa m e velocità iniziale vo che scivola su un piano.
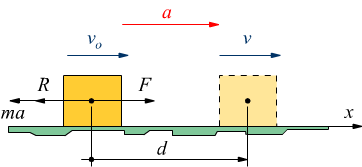
Una forza costante F lo tira in direzione dell'asse x aumentandone la velocità fino a raggiungere una velocità v per una distanza d. Una forza di attrito dinamico R che agisce sul pavimento si oppone allo spostamento del blocco; si avrà
![]()
dato che le forze sono costanti lo è anche l'accelerazione , possiamo allora usare l'equazione cinematica del moto rettilineo accelerato
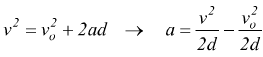
sostituendo
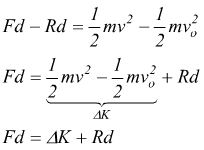
![]() incremento
di energia termica per attrito
incremento
di energia termica per attrito
Una forza applicata trasferisce energia. La forza di attrito ne converte una parte in energia termica; quindi il lavoro svolto dalla forza finisce in parte in energia meccanica e in parte in energia termica.
Per definizione l'energia meccanica di un sistema è la somma della sua energia cinetica e della sua energia potenziale.
![]()
L'energia totale di un sistema isolato, in un determinato istante, è considerata come la somma dell'energia meccanica Em, dell'energia termica Et e della sua energia interna Ei.
![]()
Ricordiamo che l'energia interna (Ei) di un sistema è la somma delle energie cinetiche e di interazione delle diverse particelle appartenenti a quel sistema. Generalizzando le considerazioni precedenti se eseguiamo un lavoro L sul sistema, il principio di conservazione dell'energia può essere riformulato nel seguente modo:
![]()
in genere, per i sistemi meccanici macroscopici la variazione di energia interna può essere trascurate e si pone ΔEi≅0 come possiamo notare nella seguente simulazione eseguita su un piano inclinato.
 edutecnica
edutecnica