Grandezze elettriche alternate sinusoidali
In un conduttore rettilineo di lunghezza l immerso in un campo magnetico con vettore induzione costante B che si muova con velocità v nel piano perpendicolare alle linee di induzione e con direzione perpendicolare al conduttore stesso, si induce una forza elettromotrice e(t) (variabile nel tempo) data dalla:
![]()
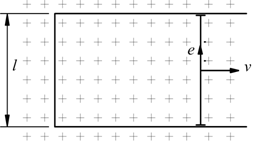

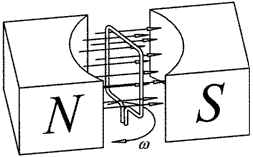
Allo stesso tipo di fenomeno andremmo incontro se facessimo ruotare una spira chiusa all'interno di un campo magnetico costante. La legge di Faraday afferma che la forza elettromotrice indotta in tal caso nella spira è proporzionale alla variazione del flusso ϕ magnetico del campo 'abbracciato' dalla spira nell'unità di tempo.
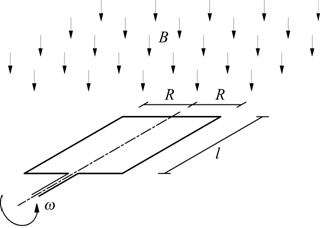
La spira ruota in un campo magnetico uniforme, con velocità angolare ω con
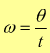
Il conduttore che taglia le linee del campo magnetico ha lunghezza l.
Ma come possiamo valutare la velocità di attraversamento delle linee del
campo in questo caso?
Prima di tutto calcoliamo la velocità periferica del tratto l della spira,
rispetto al campo magnetico B:
![]()
ovviamente vp è un vettore di modulo (intensità) costante, ma la sua direzione e verso dipendono dalla posizione del tratto l della spira rispetto al campo B.
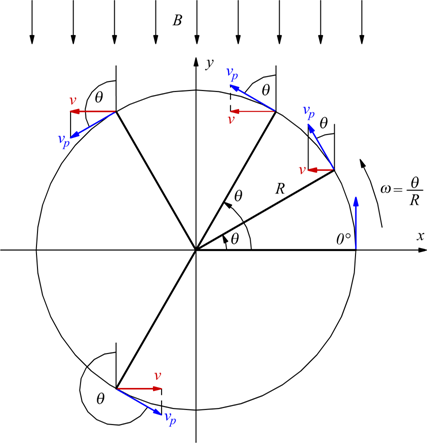
Osservando l'immagine è facile dedurre che $v=v_psinθ=ω⋅Rsinθ$
La f.e.m. indotta sarà dunque $e=Blv=B⋅l⋅ω⋅Rsinθ$
essa dipende dal tempo dato che $θ=ωt$
![]()
abbiamo posto per comodità $V=Blω$ ovviamente V=cost. dato che ω=cost. e in ragione di ciò, e dipende esclusivamente da t. La rappresentazione di e(t) in funzione di θ=ωt e:
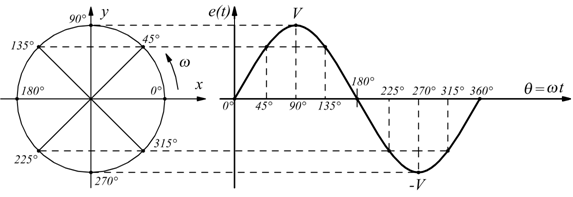
essa è riconducibile alla posizione del punto terminale
di un segmento di lunghezza costante V che mantiene un estremo, fisso
nell'origine delle coordinate e ruota lungo il perimetro di una circonferenza,
con velocità angolare ω .
Da notare come il valore massimo del segnale elettrico e(t) sia
V in corrispondenza di 90° mentre il minimo è -V in corrispondenza
di 270°.
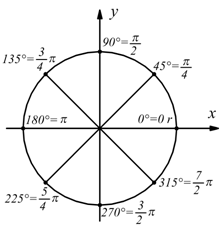
ovviamente essendo ω misurata in rad/sec occorre abituarsi
a valutare gli angoli indifferentemente in radianti o in gradi sessagesimali.
In figura è riportata la corrispondenza fra gradi e radianti per
alcuni angoli principali.
In ogni caso per effettuare le conversioni si usi il rapporto:
$$π/180={rad}/{gradi}$$
$${rad}=π/180⋅{gradi}$$ per trovare i radianti partendo dai gradi
$${gradi}=180/π⋅{rad}$$ per
trovare i gradi partendo dai radianti
Fase
La fase è una misura angolare che caratterizza la posizione del segmento V ad ogni istante della sua rotazione, Particolare importanza assume il valore della fase iniziale ϕ :la fase che caratterizza il vettore all'istante t=0.
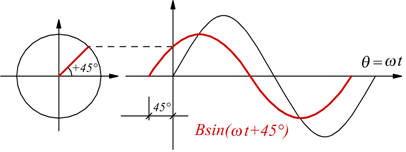
esempio di sinusoide in anticipo di fase di 45° rispetto alla sinusoide originaria di fase 0: Vsin(ω t).
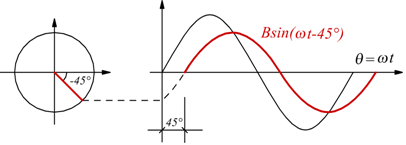
esempio di sinusoide in ritardo di fase di 45° rispetto alla sinusoide originaria di fase 0: Vsin(ω t).
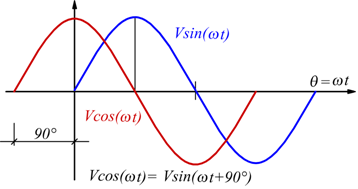
E' importante notare come sia indifferente usare la funzione seno o quella coseno per descrivere grandezze di questo tipo, data l'esistenza della relazione:
![]()
e di altre.
Periodo e frequenza
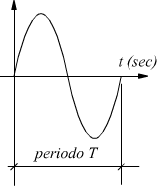
Il periodo di un'onda sinusoidale è il tempo impiegato dall'onda per compiere
un intero ciclo, l'onda è caratterizzata dal fatto che compie lo stesso
ciclo in modo ripetuto. Il ciclo di un'onda alternata si misura in secondi.
Un altro importante parametro è la frequenza che è il numero di cicli compiuti
nell'unità di tempo (in 1 secondo).
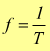 [Hertz] [Hz]
[Hertz] [Hz]
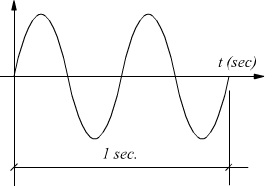
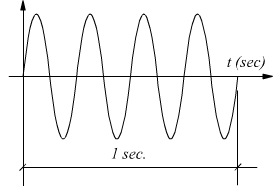
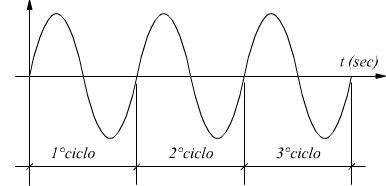
in figura la sinusoide di destra compie un numero di cicli
doppio rispetto alla sinusoide di sinistra: essa ha un periodo che è la
metà della sinusoide di sinistra.
Importante è la relazione fra frequenza, periodo e pulsazione:
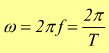
Valore efficace
Nelle grandezze elettriche in regime alternato sinusoidale molta importanza riveste la nozione di valore efficace.
Si definisce valore efficace di una grandezza alternata sinusoidale il corrispondente valore costante che produce gli stessi effetti termici prodotti dalla grandezza alternata sinusoidale.
Infatti, la potenza dissipata su una resistenza R, in corrente continua vale $P=RI^2$.
In un periodo T si sviluppa una energia termica pari a $W_c=RI^2T$.
Se valutiamo l'energia prodotta nello stesso periodo da una corrente alternata sinusoidale i=i(t) , in termini incrementali avremo:
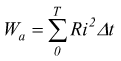 in
termini infinitesimali sarà
in
termini infinitesimali sarà 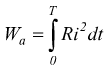 ; deve
essere:
; deve
essere:
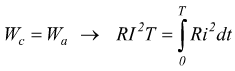 quindi
quindi
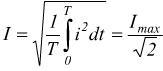 infatti
infatti
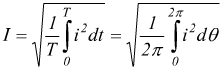 essendo
essendo
![]() si
ha
si
ha
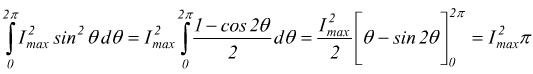
per cui 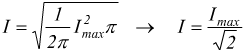 di
conseguenza,
di
conseguenza,
il valore efficace di una corrente alternata sinusoidale
vale 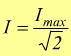 .
.
Il valore efficace di una tensione alternata sinusoidale
vale 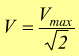 .
.
Si ricorda che il valore delle grandezze elettriche viene fornito sempre sotto forma di valore efficace.
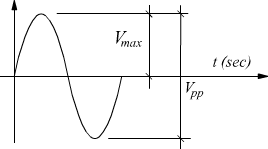
Valore picco a picco
Più intuitiva è la nozione di valore 'picco a picco' di una sinusoide.
![]()
L'elaborazione delle grandezze alternate sinusoidali è facilitata dalla teoria matematica dei numeri complessi.
Forma simbolica
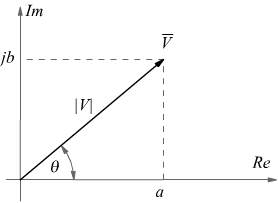
La grandezza elettrica, viene in questo caso rappresentata sul
piano dei numeri complessi tramite un vettore V che ha il suo punto
di applicazione nell'origine degli assi.
Il vettore V può essere definito con le sue due proiezioni sugli
assi cartesiani, scrivendo:
![]()
dove j è l'operatore immaginario $j=√{-1}$ a viene chiamata la parte reale di V, mentre b è la parte immaginaria di V. Questa, viene detta forma binomiale del vettore V.
Dobbiamo immaginare questa, come la posizione iniziale del vettore rotante, all'istante t=0.
Una forma alternativa a quella binomiale, è la forma polare:
![]()
dove |V| è il modulo del vettore, cioè la sua lunghezza,θ
è la fase iniziale del vettore ed e=2.718.. è il numero di Neper.
La forma binomiale e quella polare sono legate dalle relazioni:
![]()
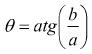
mentre (per la trigonometria)
![]()
Da queste considerazioni si deduce che possiamo definire una grandezza alternata sinusoidale, attraverso almeno tre forme:
forma sinusoidale: ![]()
forma vettoriale binomiale: ![]()
forma vettoriale polare: ![]()
La forma binomiale risulta opportuna per la somma o la differenza fra vettori, la forma polare risulta opportuna per la divisione e la moltiplicazione fra vettori.
Resistenza
Se si applica una tensione sinusoidale ai capi di una resistenza, la corrente prodotta è sinusoidale ed è in fase con la tensione:
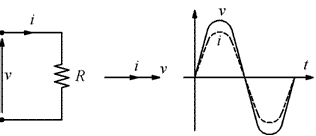
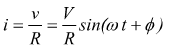
Reattanza induttiva
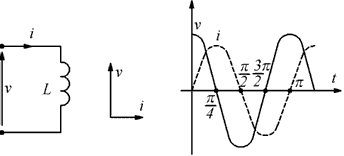
Se si applica una tensione sinusoidale ai capi di una induttanza L, la
corrente ottenuta è sinusoidale in ritardo di 90° ![]() rispetto
alla tensione e la reattanza offerta dall'induttanza vale:
rispetto
alla tensione e la reattanza offerta dall'induttanza vale:
![]() [Ω]
[Ω]
se la tensione applicata è ![]()
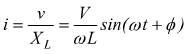
usando i numeri complessi si scriverebbe:
![]() quindi:
quindi:
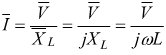
Reattanza capacitiva
Se si applica una tensione sinusoidale ai capi di un condensatore C la
corrente impressa è sinusoidale, in anticipo di 90° ![]() rispetto
alla tensione e la reattanza del condensatore è:
rispetto
alla tensione e la reattanza del condensatore è:
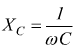
se la tensione applicata è ![]()
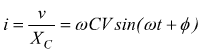
usando i numeri complessi si avrebbe:
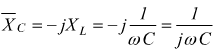 quindi:
quindi:

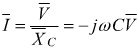
Impedenza
Una volta acquisito che la reattanza offerta da un'induttanza e da un condensatore valgono
![]() [Ω]
[Ω]
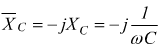 [Ω]
[Ω]
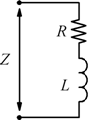
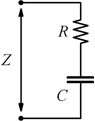
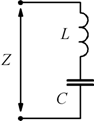
Si può risalire all'impedenza Z offerta da circuiti anche complessi.
Alcuni esempi immediati sono i seguenti:
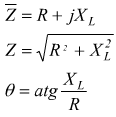
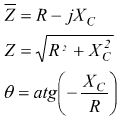
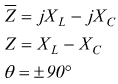
 edutecnica
edutecnica