Varianza

              

Il   valor medio di una variabile statistica x=M(X)=μ fornisce una previsione del valore più probabile che si ottiene in un gran numero di prove, ma non da indicazioni di quanto un generico valore della variabile può differire dal suo valor medio.
Data una variabile casuale X, si definisce   scarto  la differenza fra un qualsiasi valore x_i della variabile e il valor medio μ.

( x_i - μ ) =x'≡ scarto

in una distribuzione statistica, il valor medio della variabile scarto è sempre uguale a zero.
La dispersione dei valori attorno alla media (speranza matematica) sarà tanto minore quanto più piccole sono queste quantità. Dato che queste quantità sono in parte negative, viene preso in considerazione il quadrato per ottenere un valore indipendente dal segno.

La varianza σ² viene definita come

La varianza identifica la dispersione dei valori della variabile X attorno al valor medio.
Tanto più piccola è la varianza, tanto più i valori della variabile sono concentrati attorno al valor medio.

Se i valori x_i hanno frequanze diverse, cioè appaiono più volte nelle osservazioni con x₁ che ha frequenza f₁ con x₂ che ha frequenza f₂ e così via le probabilità pi sono ottenute come:

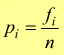   quindi la formula della varianza può anche essere espressa come:

Poichè la varianza è una quantità di secondo grado, si preferisce spesso usare la deviazione standard o scarto quadratico medio denominato semplicemente σ.

  Riassumendo   :

● La varianza è uguale a zero quando tutti i valori della variabile sono uguali e quindi non c'è variabilità nella distribuzione; in ogni caso è positiva e misura il grado di variabilità di una distribuzione.
● Tanto maggiore è la varianza tanto più i valori sono dispersi.
● Tanto minore è la varianza tanto più i valori di X sono concentrati attorno al valor medio.
● La varianza viene usata nella teoria delle decisioni come misura della rischiosità di una distribuzione.
● Se due distribuzioni hanno la stessa media e varianza diversa, la distribuzione con varianza maggiore è la più rischiosa (lo scarto è maggiore).

   Esempio   : calcolare valor medio μ e varianza σ² per la seguente distribuzione:

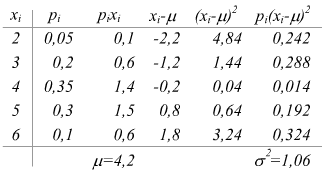
Teorema di Bienayme-Cebicev

              

Come si vede dall'esempio se abbiamo la distribuzione di probabilità di una variabile casuale è possibile calcolare i due valori che interessano μ e σ. Talvolta, può accadere di essere nelle circostanze opposte: si è in possesso del valor medio e della varianza ma non si conosce la distribuzione di probabilità. Quest'ultima eventualità non è risolvibile, anche se è possibile, tramite la disuguaglianza di Cebicev  avere una relazione tra la varianza e gli scarti della variabile X e il valor medio μ ,ottenendo alcune indicazioni sulla distribuzione di probabilità.

Teorema di Bienayme-Cebicev    : se ε è un numero positivo preso arbitrariamente, la probabilità che la variabile casuale X assuma valori che differiscano in valore assoluto dal suo valor medio più di ε non supera la varianza divisa ε².

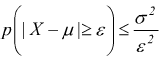    A

che si può anche scrivere anche in base alla probabilità contraria come :

    B

questo teorema (che qui non dimostriamo) è valido sia che la variabile aleatoria sia discreta che continua.

Esempio    : calcolare la minima probabilità che una variabile aleatoria X differisca dal suo valor medio μ per meno di 3σ

Se poniamo nella B ε=3σ

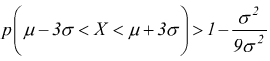
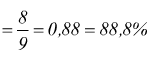
si può quindi dire che la probabilità che i valori della X differiscano da μ per meno di 3σ è maggiore dell'88,8%.