Misure di tendenza centrale

      

Le misure di tendenza centrale mirano a sintetizzare la "posizione del centro ideale" sul quale tendono a gravitare gli elementi della distribuzione di una variabile casuale e devono fornire, in relazione al fenomeno che si conosce, una visione d'insieme di tutti gli elementi.



le misure del primo gruppo tengono conto di tutti i valori della distribuzione.
Le misure appartenenti al secondo gruppo si ottengono scegliendo particolari elementi della distribuzione.

Le misure di tendenza centrale vengono anche indicate con il termine medie o valori medi in quanto soddisfano sempre alla seguente definizione alla definizione di media data dal matematico Cauchy:
Si chiama media tra più quantità date una quantità compresa tra la maggiore e la minore delle quantità considerate.

Media aritmetica

              

Si definisce media aritmetica di più numeri, quel valore che sostituito ai dati lascia invariata la loro somma.

Il significato della media aritmetica è di equipartizione della somma indicando con x₁, x₂,… x_n i numeri dati si deve avere:

per cui:

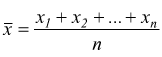             media aritmetica semplice     

una proprietà importante della media aritmetica è che la somma degli scarti è uguale a zero:

un'altra proprietà è che la somma dei quadrati degli scarti è minima rispetto a qualsiasi altro numero.

Se i valori x_i hanno frequenze diverse, cioè appaiono più volte nelle osservazioni, con x₁ che ha frequenza f₁ e x₂ con frequenza f₂ e così via, la condizione di invarianza della somma diventa:

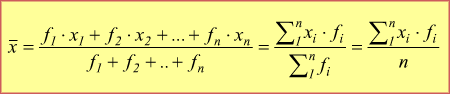      media aritmetica ponderata    

Si chiama media aritmetica ponderata, perchè le varie frequenze f_i sono dette anche "pesi".
Si riconosce come la media aritmetica semplice, non sia altro che un caso particolare di media aritmetica ponderata con valori di f_i=1 , per ciascuna ricorrenza dei valori x_i della variabile statistica studiata.

Si nota che cioè il rapporto tra la frequenza con cui si manifesta una ricorrenza x_i ed il numero totale degli eventi n, non è altro che la probabilità che ha il valore x_i di manifestarsi, di conseguenza si può anche dire

Il valor medio ( anche chiamato valore atteso o valore vero) può essere indicato a secondo delle circostanze col simbolo μ o con M(X).

Media geometrica

              

Serve per riassumere distribuzioni di dati i cui valori variano con progressione geometrica.
E' usata ad esempio per misurare il tasso di incremento o di decremento di un fenomeno.
Deriva dall'equipartizione del prodotto: se i valori sono tutti positivi e non nulli si può calcolare la media geometrica.

Si definisce media geometrica dei valori x₁, x₂,..x_n quel numero G che sostituito ai valori di x_i
lascia invariato il loro prodotto.

     da cui si ricava:

            media geometrica semplice   

se i vari x_i hanno frequenze o pesi f_i:

                media geometrica ponderata   

con      

G viene usata per rappresentare valori riferiti a dati moltiplicativi, caratterizza distribuzioni in in cui dati variano in progressione geometrica.

Media armonica

              

E' usata quando i dati sono inversamente proporzionali al fenomeno che si sta osservando
Media armonica semplice:

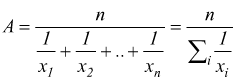
in presenza di frequenze f₁,f₂,..,f_n avremo la media armonica ponderata :

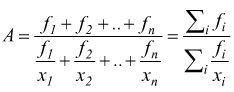
Media quadratica

              

Viene usata quando i dati si presentano con segni positivi e negativi, ed è quindi necessaria una media indipendente dal segno.
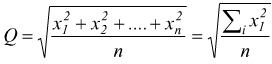      media quadratica semplice  
in presenza di frequenze avremo la media quadratica ponderata
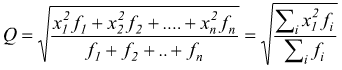     media quadratica ponderata