Teoria degli errori

Fra i tanti campi di applicazione che si avvalgono del calcolo statistico vi è la teoria degli errori; strettamente legata alla sperimentazione scientifica e alla produzione industriale.

La teoria degli errori riguarda la misurazione di grandezze fisiche, quindi lunghezze, masse, tempi etc.
Queste operazioni di misurazione di una grandezza fisica, sono in generale affette e soggette ad errori.
Qualunque sia il metodo di misurazione di una grandezza, non si può dire che il valore sia esatto, ma viene trovato con un grado di maggiore o minore approssimazione.
Se μ può essere considerato il valore vero o esatto della grandezza fisica da misurare, il valore x misurato sarà quasi sempre diverso da μ.

Si definisce in questo modo l'errore ε che può essere negativo o positivo, come differenza tra il valore vero e il valore misurato.
Se sono conosciute le cause dell'errore, l'errore stesso può essere corretto, ma nella maggior parte dei casi questo non è possibile ma dalla misurazione si può determinare una fascia di incertezza in cui è compreso il valore vero:

Gli errori possono essere sistematici o casuali:

Gli errori sistematici avvengono sempre nello stesso senso o sempre per difetto o sempre per eccesso.
Sono in genere dovuti al cattivo funzionamento dello strumento di misura oppure a degli errori personali di lettura.
Gli errori sistematici si possono eliminare se viene individuata la loro causa come ad esempio nel caso degli errori di taratura. In ogni caso è meglio eseguire la misura con due metodi diversi ed indipendenti.

Gli errori casuali variano in modo imprevedibile da una misura all'altra e influenzano il risultato qualche volta per eccesso e qualche volta per difetto. Le cause di queste differenze, anche se le misure sono eseguite in modo accurato, sono dovute a fattori imprevedibili come piccole variazioni delle condizioni ambientali, perturbazioni elettriche.

Per effettuare le misure possono essere usate diverse tecniche
• misurazione unica
• n misurazioni
• misure effettuate con strumenti diversi

Misurazione unica

La sensibilità di uno strumento è il più piccolo valore della grandezza che lo strumento può distinguere. Se si esegue una sola misura di una grandezza con uno strumento a bassa sensibilità (ottenendo quindi sempre lo stesso valore) . La misura viene espressa come :

dove Δx è l'errore massimo o errore assoluto della misura: esso coincide con la sensibilità dello strumento.
Oltre all'errore assoluto si determina l'errore relativo δ che è dato dal rapporto tra l'errore assoluto e il valore assoluto della grandezza misurata .

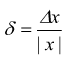
Ad es. se si misura una sbarra di metallo con un comune metro a nastro graduato in millimetri, sapendo che l'errore massimo che si può effettuare è di 1 mm, se la misura rilevata è di 18,7 cm si scriverà:

L'errore relativo è il rapporto tra l'errore massimo e il valore medio mentre l'errore assoluto è espresso con la stessa unità di misura del valore della grandezza, l'errore relativo è un numero puro.
L'errore relativo è più significativo dell'errore assoluto per indicare la precisione di una misura: più l'errore relativo è piccolo, più la misura è precisa.

Valore di una misura mediante n misurazioni

Se si fanno diverse misure, si sceglie come risultato il loro valore medio, che è il rapporto tra la somma delle misure e il numero delle misure.

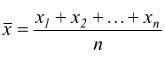
Nella teoria della stima si dimostra che la media aritmetica è la stima migliore del valore vero della misura della grandezza X che si sta misurando.
Nel caso di n misurazioni, per stimare l'errore di misura si considera lo scarto quadratico medio corretto:

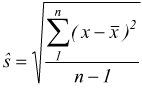chiamato anche scarto standard

Notiamo come lo scarto standard sia leggermente superiore alla deviazione standard, perchè al denominatore c'è n-1 invece che n.
La misura della grandezza X in base alle n misurazioni viene espressa come

più lo scarto standard è piccolo più la misura è precisa. Lo scarto standard è anche detto errore sperimentale.
Dallo scarto standard , si ottiene lo scarto standard relativo (errore relativo):

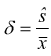
Lo scarto standard è anche chiamato errore sperimentale. .

n :

Misura con metodi diversi

Spesso la stessa grandezza viene misurata con metodi diversi o con strumenti diversi. In genere , i risultati ottenuti differiscono fra loro a causa della diversa sensibilità degli strumenti di misura.

Ogni misura viene ottenuta calcolando la media aritmetica di varie misurazioni e lo scarto standard:

Si può dimostrare che la miglior stima della misura della grandezza X si ottiene facendo la media aritmetica ponderata delle medie, assumendo come pesi i reciproci dei quadrati degli scarti standard:

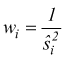cioè si ha

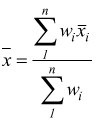con associato come errore standard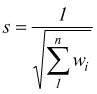

La misura effettuata con il metodo della media ponderata (media pesata) viene poi espressa come

Cifre significative

Il valore ottenuta da una misurazione viene espresso da un numero decimale limitato con un certo numero di cifre significative.

Il numero di cifre significative si ottiene contando tutte le cifre a partire da destra fino all'ultima fino all'ultima cifra a sinistra diversa da zero.

Numero	Cifre significative
12	2
22,5	3
19,40	4
7620	4
0,3	1
0,02	1
200,24	5

Le cifre significative sono le cifre certe e la prima cifra incerta

in questo caso le cifre significative sono 3: le cifre certe sono 2 e quelle incerte 1.

Nelle applicazioni si usano alcune regole pratiche per determinare il numero di cifre significative dell'errore standard e della misura:

• gli errori standard, dovrebbero essere normalmente arrotondati ad una cifra significativa o al massimo a due.

• il risultato di una misura può avere tante cifre significative quante sono necessarie, ma la cifra significativa di posto più basso deve essere nella stessa posizione della cifra dell'errore standard (errore assoluto).

Ad es. non ha senso dare la misura di una massa scrivendo

ma si deve scrivere

Se ad es. si è ricavata la media con si scrive

se invece l'errore standard fosse stato avremmo scritto

Propagazione degli errori

Se Y è la grandezza somma o differenza delle grandezze A e B.

Errore sulla somma e sulla differenza
Si ha che l'errore massimo assoluto della somma o della differenza delle misure di più grandezze è uguale alla somma degli errori massimi delle misure delle grandezze.

somma

differenza

Errore sul prodotto e sul quoziente
L'errore relativo sul prodotto o sul quoziente di due misure è uguale alla somma degli errori relativi sulle singole misure.

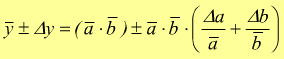prodotto

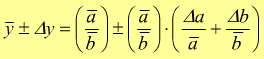quoziente

Interpretazione statistica degli errori di misura

Se si eseguono molte misure di una grandezza nelle stesse condizioni e queste misure si rappresentano graficamente, si ottiene un istogramma che è approssimato da una curva normale (gaussiana).

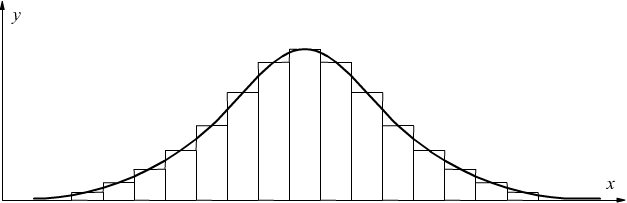
L'approssimazione dell'istogramma con la curva normale è tanto maggiore quanto più grande è il numero di misure e quanto più piccola è l'ampiezza degli intervalli.

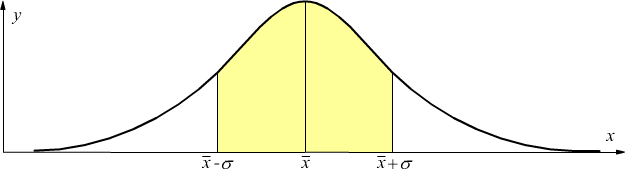
Il 68,3% delle misure effettuate è compreso fra i valori       ed    .
Il 95,44% delle misure effettuate è compreso fra i valori       ed    .
Il 99,73% delle misure effettuate è compreso fra i valori        ed     .

con scarto quadratico medio ( o deviazione standard )

Quando le misure sono numerose è possibile la trattazione statistica dei dati sperimentali e si sceglie come valore dell'incertezza l'errore standard della media

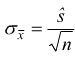anche se a volte si semplifica ponendo ŝ= σ.

E' possibile, dopo aver calcolato il valore medio di n misure ed il valore dell'errore standard della media, determinare un intervallo di che contenga il valore vero μ con un certo intervallo di fiducia. Queste considerazioni sono valide solo se la popolazione dei campioni è un numero n > 30. In tal caso l'intervallo della media che contiene il valore vero μ è dato da

dove z_c è il valore di z che corrisponde ad un livello fissato di fiducia. Si ha:

Ad es. con un livello di fiducia al 95% si ha
con un livello di fiducia al 99% si ha

Se n ≤ 30 si dimostra che la distribuzione delle medie segue la distribuzione di Student con ν=n-1 gradi di libertà. Si ricava in modo analogo l'intervallo di μ ad un certo livello di fiducia, però in questo caso il valore di t_c dipende dai gradi di libertà. L'intervallo della media è

con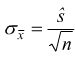

Esempio: si sono eseguite 50 misure sulla resistenza elettrica di un conduttore e si è ricavato un valor medio ed un errore standard:

Calcolare l'intervallo che contiene il valore vero della grandezza con pratica certezza
( con livello di fiducia del 99,73% ).

Soluzione: a livello di fiducia del 99,73% si ha:

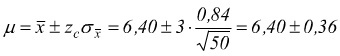
Si ha quasi la certezza che la resistenza sia compresa fra 6,76 e 6,04 Ω.

Esempio: sono state eseguite 10 misure di velocità di un punto materiale e sono stati rilevati i seguenti valori per la media aritmetica e l'errore standard:

Determinare l'intervallo della velocità ad un livello di fiducia del 95%.

Soluzione:l'intervallo per la misura della velocità è

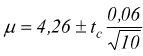
Si cerca sulla tabella di Student il valore di t_0,95 con 9 gradi di libertà trovando t_0,95=2,26 e si ha μ=4,26±0,04. La velocità risulta compresa tra 4,22 m/s e 4,30 m/s ad un livello di fiducia del 95% (livello di significatività del 5%).