Correlazione
Mentre la regressione determina una funzione, la correlazione conduce a misurare la forza del legame tra due variabili.
Si definisce coefficiente di correlazione lineare di Bravais-Pearson il rapporto tra la covarianza di X e di Y e il prodotto degli scarti quadratici medi (dev.std.) di X e di Y.

Se chiamiamo come al solito lo scarto x'i=(xi-μ) ricordando che
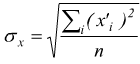 e
e 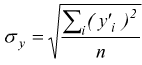 si
ha
si
ha

L'indice di correlazione r ha le seguenti proprietà
• è un valore dimensionale e non dipende dalle dimensioni di X
o Y
• ha un valore compreso tra -1 e +1 : -1 ≤ r ≤ +1
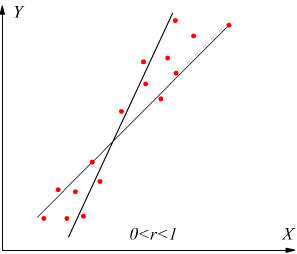
• se r > 0 la correlazione è diretta o positiva
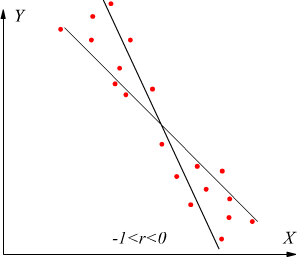
• se r < 0 la correlazione è inversa o negativa
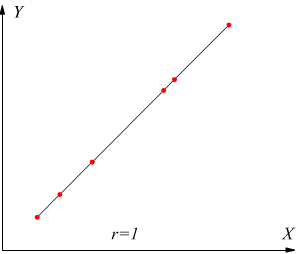
• se r=1 la correlazione è perfetta diretta
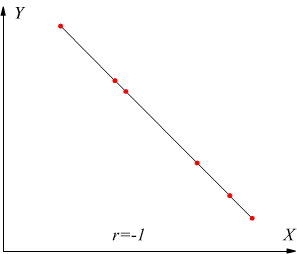
• se r=-1 la correlazione è perfetta inversa
• se r=0 non esiste correlazione lineare, potrebbe però esistere
una correlazione curvilinea, cioè le due variabili potrebbero essere
legate da una relazione di tipo parabolico o di tipo esponenziale. etc.
Tenendo presente l'espressione delle due rette di regressione:
y=a+bx
x=c+dy
un'altra importante proprietà del coefficiente di correlazione lineare è
![]()
quindi, r è la media geometrica dei due coefficienti di regressione, preceduta da '+' se o due coefficienti sono positivi e dal segno '-' se i due coefficienti sono negativi, infatti se eseguiamo il prodotto dei coefficienti di regressione lineare.
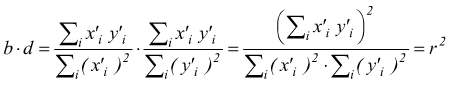


coefficiente di determinazione
Consideriamo la varianza della variabile Y

Contrassegnando con![]() i valori di Y teorici per ciascun xi e contrassegnando con
yi i valori rilevati della Y, per ciascun valore xi
dal grafico si vede come sia
i valori di Y teorici per ciascun xi e contrassegnando con
yi i valori rilevati della Y, per ciascun valore xi
dal grafico si vede come sia ![]() dunque
dunque
![]()
elevando al quadrato e sommando per n punti
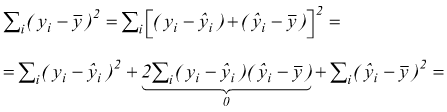
E' possibile dimostrare in base al metodo dei minimi quadrati che il termine indicato è nullo. Si ha in definitiva

La varianza ![]() della
variabile Y si decompone in una parte
della
variabile Y si decompone in una parte![]() detta varianza spiegata, in quanto la variabilità della Y è dovuta alla
dipendenza di Y da X; e in una parte
detta varianza spiegata, in quanto la variabilità della Y è dovuta alla
dipendenza di Y da X; e in una parte ![]() detta
varianza non spiegata in quanto la variabilità della Y non dipende dalla
X ma da altri fattori.
detta
varianza non spiegata in quanto la variabilità della Y non dipende dalla
X ma da altri fattori.
Come si può notare

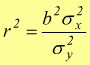 coefficiente
di determinazione
coefficiente
di determinazione
Il coefficiente di determinazione, indica quale frazione di varianza totale è dovuta alla dipendenza lineare tra Y ed X, cioè indica quanto il modello di regressione lineare è aderente al fenomeno empirico che si sta studiando. Tanto più r2 è prossimo ad 1 tanto maggiore è la 'bontà' del modello lineare.
Esempio : nella tabella vi sono le rilevazioni del profitto e delle spese ( in mln.di Euro) sostenute da n=6 aziende calcolare il coefficiente di regressione e valutare il leagame tra le due variabili.
| azienda | profitto | spese |
| A | 50 | 20 |
| B | 60 | 40 |
| C | 30 | 14 |
| D | 85 | 50 |
| E | 95 | 60 |
| F | 40 | 26 |
Dalla tabella successiva
| azienza | x | y | x’ | y’ | x’y’ | (x’)2 | (y’)2 |
| A | 50 | 20 | -10 | -15 | 150 | 100 | 225 |
| B | 60 | 40 | 0 | 5 | 0 | 0 | 25 |
| C | 30 | 14 | -30 | -21 | 630 | 900 | 441 |
| D | 85 | 50 | 25 | 15 | 375 | 625 | 225 |
| E | 95 | 60 | 35 | 25 | 875 | 1225 | 625 |
| F | 40 | 26 | -20 | -9 | 180 | 400 | 81 |
| tot | 360 | 210 | 2210 | 3250 | 1622 |
applicando il metodo dei minimi quadrati si ottiene


le rette di regressione sono
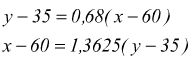 con
con
![]()
La correlazione può essere ritenuta molto buona, inoltre è r2=0,9265 dunque il 92,65% della varianza di Y è spiegata dalla dipendenza con la X. Il legame tra le due variabili può essere considerato forte.
 edutecnica
edutecnica