Connessione tra variabili statistiche

     

Un importante studio, nel calcolo statistico è la connessione tra due variabili, che può essere effettuato o ricercando se una variabile dipende da un'altra o se le due variabili si influenzano reciprocamente.

Lo studio della regressione consiste nella determinazione di una funzione matematica che esprime la relazione tra due variabili.

La regressione, è molto utile, perché permette di valutare, entro i limiti dell'intervallo dei dati rilevati, il valore della variabile dipendente al variare della variabile indipendente.

La correlazione può, invece, essere assimilata alla 'forza' o all'intensità che interviene nel legame tra due variabili. La correlazione può essere misurata attraverso vari indici, il più importante dei quali è il coefficiente di correlazione lineare.

Lo studio della correlazione, può spesso precedere quello della regressione, perché si tenta di confrontare una variabile con diverse altre per trovare la migliore connessione.

Regressione

          

Ipotizziamo due variabili statistiche X ed Y considerando le coppie (x_i,y_i) associate. Per prima cosa occorre fare un diagramma rappresentativo dei valori (x_i,y_i) rilevati, ottenendo in questo modo il diagramma a dispersione.

               

 

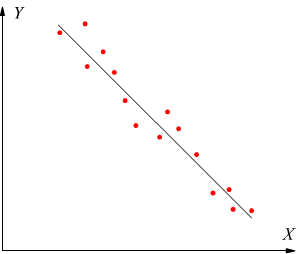
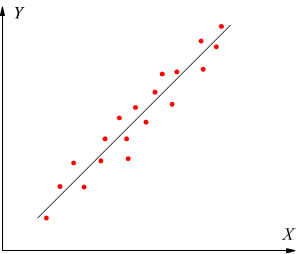
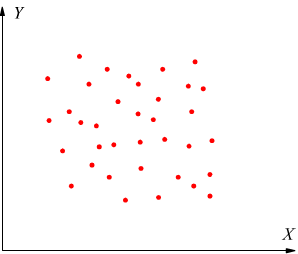
Se esiste una relazione lineare, i punti si distribuiscono vicino ad una retta, come si vede dai primi due schemi.

Se invece, i punti sono molto dispersi, come nel terzo schema, non esiste alcuna relazione

 

 

 

Metodo dei minimi quadrati

     

Se in corrispondenza dei valori x_i rilevati si hanno .

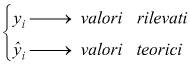
Per il metodo dei minimi quadrati l'accostamento migliore viene ottenuto minimizzando la somma dei quadrati delle differenze tra i dati osservati e i dati teorici.

             

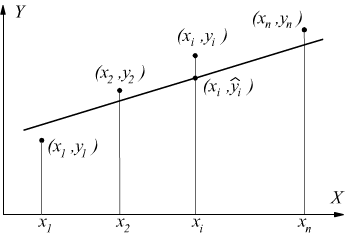
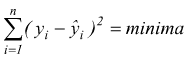
L'applicazione più comune del metodo dei minimi quadrati, consiste nel ricondurre il legame tra le due variabili x ed y ad una funzione lineare del tipo y=a+bx. Si deve dunque minimizzare la funzione:

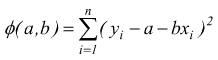
per il calcolo del minimo, si dovranno valutare le derivate parziali prime rispetto ad a e b di questa funzione e dopo aver applicato gli opportuni criteri si dimostra che questa funzione ha minimo per i valori a,b:

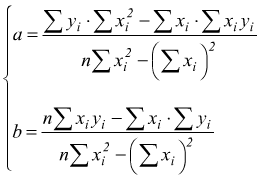
l'equazione della retta interpolante ( o perequatrice tra i punti noti ) è:

     dove       

è possibile dimostrare che i valori a e b possono essere espressi anche in funzione degli scarti x' ed y':

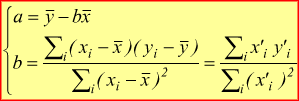
Da quest'ultima forma rappresentativa si riesce ad osservare che

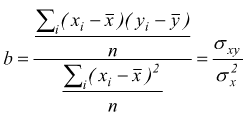
σ_x²= varianza di X mentre il numeratore viene definito covarianza di X ed Y.

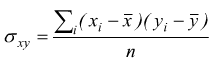
Mentre la varianza misura la variabilità dei valori di X rispetto al valor medio, la covarianza esprime la variabilità congiunta delle coppie (x,y) di valori corrispondenti rispetto al loro valor medio:

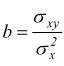
Il coefficiente b della retta interpolante esprime quindi la variabilità congiunta delle due variabili X ed Y rapportata alla variabilità della sola X.

In questo caso è stata studiata la retta di regressione di Y rispetto ad X con b definito come coefficiente di regressione di Y rispetto ad X. In modo analogo si può studiare la retta di regressione di X rispetto ad Y, di equazione:

     con       

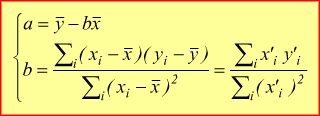
La retta di regressione di X rispetto ad Y si può anche scrivere come

d viene detto coefficiente di regressione di X rispetto ad Y.
I due coefficienti b e d hanno lo stesso segno, perché questo dipende dal numeratore che è uguale.
Se b e d sono positivi quando una variabile cresce, cresce anche l'altra, se invece sono negativi, quando una variabile cresce, l'altra diminuisce. In analogia alla retta di regressione di Y rispetto ad X si può dimostrare che è

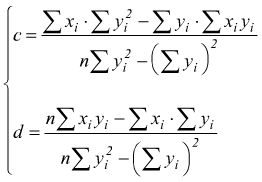
  Esempio  : studiare le rette di regressione delle due variabili

x	25	36	39	50	50
y	12	21	27	42	48