Un'onda che avanza in una data direzione è chiamata onda progressiva. Un'onda può essere generata quando in un mezzo elastico si genera un disturbo che rilascia energia. L'onda progressiva trasferisce energia attraverso il mezzo allontanandosi continuamente dalla sorgente del disturbo, si pensi ad esempio alla classica onda che si forma sulla superficie di uno specchio d'acqua quando viene lanciato in esso un sasso.
In un mezzo illimitato, l'onda progressiva viaggia continuamente in una determinata direzione fino a quando non esaurisce la sua energia.
Quando un'onda non si propaga, ma rimane sempre nella stessa regione dello di spazio è un'onda stazionaria. Si pensi ad esempio alla corda di una chitarra:toccando una corda di chitarra si generano delle onde che si propagano versoi due estremi della corda. Giunte alle due estremità, le onde si riflettono e si dirigono verso il capo opposto della corda, per generando diverse riflessioni consecutive. La sovrapposizione di queste onde, tutte della stessa frequenza, che si propagano lungo la corda, produce un'onda stazionaria.
Come già visto nella pagina sull'interferenza tra le onde, l'equazione di un' onda progressiva che si propaga nel verso positivo dell'asse x può essere espressa da una funzione trigonometrica del tipo:
1
un' onda regressiva che si propaga nel verso negativo delle x, ha equazione :
2
In un mezzo illimitato (infinito) un'onda viaggia continuamente in una data direzione fino a quando la sua energia non si esaurisce. In un mezzo limitato (finito), l'onda può arrivare al confine del mezzo e riflettersi indietro. In questo modo a un'onda progressiva di eq. 1 si sovrappone ad un'onda regressiva di equazione :
il risultato di questa sovrapposizione è
Questa sovrapposizione può produrre un'onda stazionaria, vediamo come. Per le formule di prostaferesi si ha :
dunque
poi ricordando che sin(–α) = –sinα
3
Quella appena trovata è l'equazione di un'onda che al passare del tempo ha ampiezza :
Se supponiamo che lo spazio limitato in cui agisce quest'onda varia da
x=0÷L ci saranno dei valori di x in cui si avrà ampiezza di oscillazione
2A e altri valori di x in cui l'oscillazione sarà nulla.
Sicuramente AT=0 per x=0, ma anche nell'estremo opposto x=L si
può avere AT=0 se viene rispettata la condizione :
con
n=1,2,3,. . . intero positivo
per ottenere che agli estremi AT=0 la lunghezza d'onda λ puo assumere solo i seguenti valori :
sostituendo questo valore nell'eq. 3 otteniamo l'espressione propria di un'onda stazionaria.
4
da questa equazione si deduce quali siano i punti x appartenenti all'intervallo 0÷L in cui si annulla l'ampiezza dell'onda stazionaria, basta porre
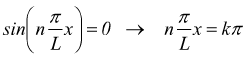con
k=0,1,2,3 . . . intero
con
0≤k≤n; quindi se si hanno
2 nodi
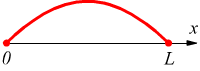
3 nodi
4 nodi
I valori x in cui l'ampiezza dell'onda stazionaria si annulla si chiamano
nodi.
I valori x in cui l'ampiezza dell'onda stazionaria è massima si chiamano
antinodi o ventri.
Le onde stazionarie soddisfano sempre precise condizioni al contorno ai
confini della regione in cui esistono.
Nel caso di una corda vibrante interessata da onde stazionarie, essa viene
fissata alle sue estremità e ha una deviazione verticale o orizzontale pari
a zero nei punti di fissaggio.