Mintermini e maxtermini

        

Ipotizziamo una funzione logica con una sola variabile di uscita Y e n variabili indipendenti di ingresso A,B,C,...

Y=F(A,B,C,..)

è definito mintermine, (termine minimo indicato con m) il prodotto in cui ogni variabile logica di ingresso appare una sola volta, complementata (negata) o non complementata a secondo che essa appaia nella tabella della verità della funzione con valore 0 o con valore 1.

Si definisce maxtermine, (termine massimo indicato con M) una somma in cui ogni singola variabile della funzione è presente complementata o non complementata a seconda che appaia nella tabella della verità con il valore 1 o con il valore 0.

La somma dei mintermini delle combinazioni che determinano un livello 1 della funzione logica costituisce la forma canonica della somma. Il prodotto dei maxtermini delle combinazioni che determinano un livello 0 della funzione logica,costituisce la forma canonica del prodotto di una assegnata tabella della verità.

Ad es. per la funzione che esprime la seguente tabella

La forma canonica della somma è

La forma canonica del prodotto è

Come si verifica facilmente, data la tabella della verità, la funzione logica associata può essere espressa tramite una di queste due forme.
La forma canonica della somma o del prodotto non è necessariamente l'espressione più semplice adatta a rappresentare una data funzione booleana.
Una funzione minimizzata comporta un circuito logico più semplice e di conseguenza a più basso costo ed ingombro rispetto a quello realizzato partendo dalla funzione non minimizzata.

Metodo di Quine - Mc Cluskey

        

Il metodo di minimizzazione delle funzioni logiche delle mappe di Karnaugh presenta notevoli difficoltà se le variabili del problema in esame diventano numerose (più di quattro) in quanto diviene complicato per l'operatore scegliere i raggruppamenti ottimali che conducono alla funzione minima.

Un metodo di minimizzazione basato sugli stessi principi di quello di Karnaugh, ma più sistematico, è quello di Quine - Mc Cluskey.
Il procedimento può essere applicato una volta assegnata la tabella della verità come ad esempio quella seguente

Si separano tutti i mintermini a valore 1 (m₀ m₁ m₈ m₉ m₁₁ m₁₄ m₁₅) in gruppi che hanno lo stesso numero di 1 e si riportano questi gruppi in ordine crescente.

Scritti i mintermini sotto forma di numeri binari e così ottenuta la tabella seguente, si confrontano sistematicamente i termini di ciascun gruppo con quelli del gruppo immediatamente superiore eliminando le variabili che cambiano di valore nella loro somma booleana.
Occorre osservare che le semplificazioni possono avvenire soltanto tra mintermini che differiscono per il valore di una sola variabile.

Ad esempio confrontando con si ottiene come risultato della somma infatti .

Si sostituiscono poi in corrispondenza delle variabili eliminate col trattino ottenendo la seguente tabella

In questa tabella sono semplificabili solamente quei termini che differiscono per il valore di una sola variabile e hanno il trattino nella stessa posizione, per esempio con .
Si arriva, allora, alla tabella qui sotto riportata nella quale non è possibile una ulteriore riduzione dei termini

I termini non più riducibili sono detti primi implicanti e sono indicati con la lettera I ed I_n l'implicante n-esimo.
Una volta ricavati i primi implicanti, in questo caso (I₁ I₂ I₃ I₄) perché i primi due termini della tabella precedente sono uguali, si sceglie poi tra questi il numero minimo che verifica la tabella della verità assegnata e che allo stesso tempo realizza la funzione minima.
Per fare questo, si disegna un reticolo composto da tante righe verticali quanti sono i mintermini considerati e tante righe orizzontali quanti sono i primi implicanti.
Si associa poi ad ogni linea verticale un mintermine e ad ogni riga orizzontale un primo implicante, come mostrato qui di seguito:

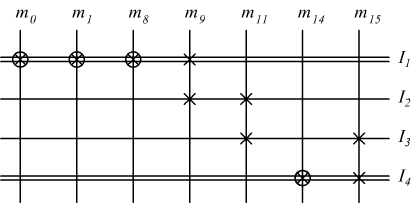
Su questo reticolo devono essere marcati con una x tutti quei mintermini che sono contenuti o coperti da ogni implicante primario.

l'implicante primario I₁ contiene i mintermini m₀ m₁ m₈ ed m₉ mentre I₂ copre m₉ m₁₁ etc.
Una volta effettuata questa operazione si individuano nel reticolo le x che si trovano da sole lungo ogni linea verticale racchiudendole in un cerchio, questo per evidenziare che il termine corrispondente fa parte di un solo primo implicante chiamato implicante essenziale, in quanto deve necessariamente comparire nell'espressione finale della funzione minima.
Eventuali mintermini non coperti dagli implicanti essenziali devono essere coperti o contenuti dagli altri implicanti primari.
L'espressione della funzione minima sarà data dalla somma degli implicanti essenziali in aggiunta ad eventuali implicanti primari che coprono eventuali mintermini rimasti scoperti.
Se ci riferiamo all'ultimo reticolo disegnato, avremo due implicanti essenziali I₁ e I₄ che coprono rispettivamente i mintermini m₀ m₁ m₈ m₉ ed m₁₄ m₁₅. Resta scoperto solo il mintermine m₁₁ , quest'ultimo, però, può essere coperto indifferentemente dagli implicanti primari I₂ o I₃.
Si ottengono, dunque, le seguenti forme minime della funzione assegnata dalla tabella della verità iniziale:

oppure

che in questo caso potrebbe anche essere verificato con il metodo delle mappe di Karnaugh.
Il metodo di Quine Mc Cluskey è particolarmente adatto ad essere automatizzato.

: Indice dei mintermini (separati da uno spazio)

: Numero di variabili

In questo caso la variabile negata viene rappresentata con un apostrofo che la segue.