Vincoli e reazioni
I vincoli sono condizioni che limitano il movimento di un corpo o di una particella nel tempo e nello spazio.
Quando un corpo non è libero di spostarsi in tutte le direzioni si
dice che tale corpo è vincolato.
Un vincolo limita, dunque, lo spostamento
di un corpo.
Un corpo vincolato è soggetto all'azione di forze, i vincoli
sviluppano forze contrarie chiamate reazioni.
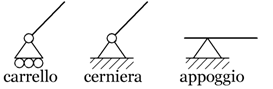
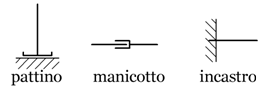
I vincoli vengono classificati in base al numero di movimenti
che essi sono in grado di impedire:traslazione verticale, traslazione
orizzontale e rotazione.
I vincoli semplici sono dati dall'appoggio
e dal carrello.
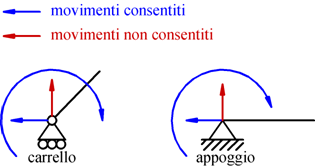
L'appoggio semplice, reagisce solo in direzione perpendicolare al
piano e impedisce i movimenti del corpo in tal senso, mentre permette
scorrimenti lungo il piano che possono essere facilitati in presenza
di rulli.
Il carrello, toglie solamente la possibilità di traslazione
sulla normale alla sua retta di scorrimento; mentre è libero di scorrere
(in senso orizzontale) e di ruotare.
l'appoggio e il carrello sono vincoli semplici
perché tolgono solo un grado di libertà; essi reagiscono dunque
con una sola reazione vincolare.
Poi esistono vincoli
doppi come la cerniera, il pattino e il manicotto.
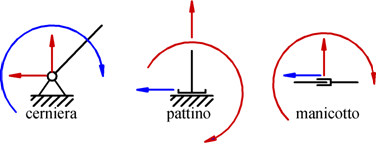
La cerniera, reagisce in qualunque direzione passante per il suo centro, permette solo la rotazione del corpo.
Come nel caso del pattino e il manicotto, toglie due gradi
di libertà. Essi reagiscono, dunque,
con due reazioni vincolari.
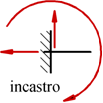
L'incastro, è vincolo triplo ; esso reagisce in qualunque direzione: sviluppa delle reazioni che impediscono qualsiasi movimento:reagisce dunque con tre reazioni vincolari.
Equazioni cardinali della statica
Se indichiamo con R la risultante delle forze attive applicate ad un
corpo ed R' la risultante delle reazioni vincolari;
se M è il momento della forze attive applicate ed M' il momento delle
reazioni vincolari;
affinché il corpo sia in equilibrio deve essere :
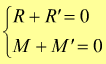
Sono valide per qualunque sistema, per qualunque tipo di vincolo, per
qualsiasi sistema di forze.
Sono necessarie per l'equilibrio di un sistema ma sono solo sufficienti
per i corpi rigidi e non per quelli deformabili.
Applicazione delle equazioni
cardinali della statica
Il caso più immediato che si può considerare è quello di un corpo (una
trave) appoggiato agli estremi e soggetto a un carico.
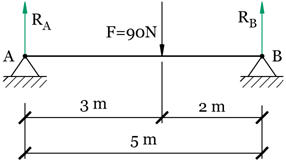
dalla prima equazione cardinale della statica avremo:
![]() quindi..
quindi..
![]() le
reazioni vincolari devono bilanciare le forze esterne
le
reazioni vincolari devono bilanciare le forze esterne
Poi, scegliamo arbitrariamente un punto rispetto al quale eseguire la
seconda equazione cardinale della statica; fulcrando la trave in A e scegliendo
positivi i momenti orari:
![]() cioè..
cioè..
![]() quindi..
quindi.. 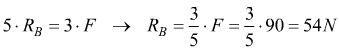
La reazione vincolare in A non contribuisce con alcun momento dato che
il suo braccio è nullo rispetto ad A. Sostituendo quest'ultimo valore
nella prima equazione avremo..
![]() per cui..
per cui.. ![]() avremo:
avremo: ![]()
allo stesso risultato si perverrebbe fulcrando la trave in B.
Carico distribuito linearmente
E' possibile determinare la risultante di carichi distribuiti, ricordando
che per una distribuzione lineare vale la regola:
![]()

dove q è il valore del carico distribuito sull'unità di lunghezza
espresso in (N/m)
Carico distribuito con legge
triangolare
Ricordiamo le regole che permettono di ricavare la risultante per un carico
distribuito con legge lineare:
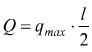

dove qmax è il
valore massimo del carico distribuito sull'unità di lunghezza (N/m).
Computo dei vincoli
Davanti ad un problema sulla valutazione della stabilità di un sistema,
abbiamo a disposizione soltanto le equazioni cardinali della statica;
quindi possiamo calcolare le reazioni vincolari solo per quei sistemi
in cui il numero di equazioni (in genere 3) uguaglia o è superiore al
numero di incognite ( in genere le reazioni vincolari).
E' possibile constatare che la posizione di un corpo rigido, su di un
piano è completamente determinata dalla conoscenza di 3 parametri (le
coordinate x,y di un suo punto e l'angolo che esso forma rispetto ad un
asse di riferimento).
In modo analogo per limitare le libertà di movimento di tale corpo occorrono
almeno 3 vincoli cioè la traslazione lungo due direzioni ortogonali e
la rotazione attorno ad un punto qualsiasi. Pertanto, possiamo contrastare
i possibili movimenti di un corpo, applicando ad esso tre vincoli semplici,
oppure un vincolo doppio e uno semplice, oppure un vincolo triplo.
E' possibile vincolare una struttura con un numero maggiore di vincoli,
rispetto a quello che sono i suoi gradi di libertà; come nel caso dell'arco
a due cerniere:
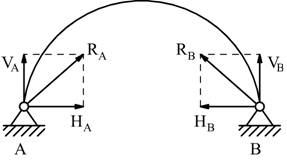
In tal caso la struttura ha 3 gradi di libertà e 4 reazioni vincolari
HA,VA,HB e VB . Una eventuale
applicazione delle equazioni cardinali, ci metterebbe a disposizione tre
equazioni in presenza di queste quattro incognite.
Secondo la Statica, questo, è un sistema indeterminato e questa struttura
viene chiamata iperstatica.
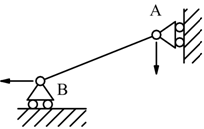
Viceversa, nella figura precedente si vede un'asta vincolata da due carrelli
che tolgono un grado di libertà ciascuno. Mancando un terzo vincolo, la
struttura è libera di muoversi e viene chiamata labile.
In generale si ha a che fare con strutture isostatiche,
con tre vincoli che è il caso strettamente necessario ad impedire ogni
tipo di movimento. Quindi, riassumendo, per un corpo rigido, chiamando
v=numero di vincoli a cui è soggetto si avrà:
![]()
a=numero di appoggi o carrelli ( 1 g.v.)
c=numero di cerniere ( 2 g.v.)
i=numero di incastri ( 3 g.v.)
Dato che per un singolo corpo rigido i gradi di libertà sono 3:
v<3 struttura labile
v=3 struttura isostatica
v>3 struttura iperstatica
E' frequente avere a che fare con sistemi strutturali composti da più
corpi rigidi vincolati fra loro tramite cerniere. In tal caso i gradi
di libertà sono l=3n, dove n è il numero di elementi componenti il sistema.
Il numero di vincoli che assoggetta il sistema è:
![]()
dove m è il numero di elementi che concorrono
in ogni cerniera.
Infatti, ogni cerniera, toglie 2 gradi di libertà ad ogni elemento concorrente,
ma può spostarsi nel piano secondo 2 direzioni conservando 2 gradi di
libertà:
![]()
per queste strutture composte:
![]() strutture
labili
strutture
labili
![]() strutture
isostatiche
strutture
isostatiche
![]() strutture iperstatiche
strutture iperstatiche
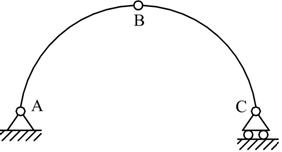
La struttura precedente è un 'arco a tre cerniere; notiamo, come essa,
sia costituita da n=2 elementi quindi i gradi di libertà sono:l=3n=6.
E' fissato con una cerniera (2g.v.) un carrello (1g.v.); viè inoltre una
cerniera interna in cui concorrono i due elementi:
![]()
La struttura è labile, dato che i gradi di libertà sono in numero maggiore
dei gradi di vincolo.
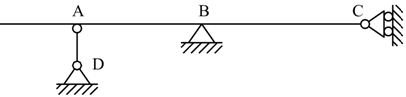
In questo non abbiamo nessun incastro; la cerniera D l'appoggio B e il
carrello C (che è come un appoggio perché toglie un solo grado di libertà),
Abbiamo un'unica cerniera interna in cui convergono i due elementi; i
gradi di libertà totali sono l=3n=6 appunto, dato che gli elementi complessivi
sono 2.
![]()
La struttura è isostatica.

La struttura riportata è sempre un arco a tre cerniere con l=3n=6 gradi
di libertà, ma stavolta, in virtù della presenza di un incastro (3g.v.)
il computo delle reazioni vincolari ci porta a scrivere:
![]()
La struttura, è in questo caso iperstatica (una volta iperstatica).
 edutecnica
edutecnica