Impulso di forza e quantità di moto
Consideriamo la seconda legge di Newton nella sua forma più semplice e moltiplichiamo entrambi i membri per il tempo t.
ma a·t=v velocità
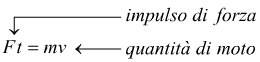
Supponiamo di voler avviare un corpo dotato di massa (m) inizialmente fermo e di voler fargli raggiungere una certa velocità (v): possiamo ottenere questo risultato in due modi:
1 usando una forza piccola applicandola per
un lungo periodo di tempo
2 usando una forza grande applicandola per un
breve periodo di tempo
Se la forza F rimane applicata per un tempo t, il corpo mobile acquista una certa accelerazione (a) che per la cinematica vale
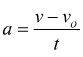
con vo=velocità iniziale e v=velocità finale acquisita ; sostituendo
I=F·t=impulso di forza
p=m·v=quantità di moto
Teorema dell'impulso: La variazione della quantità di moto è uguale all'impulso della forza che agisce su un corpo.
Queste considerazioni valgono nel caso di un singolo corpo; se in un sistema vi sono almeno due corpi come indicato nel disegno, vale il
Principio di conservazione della quantità di moto: la quantità di moto totale di un sistema composto da due particelle soggette soltanto alla loro mutua interazione rimane costante.
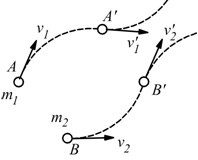all'istante
t la particella 1 si trova in A con velocità v1 e la particella
2 si trova in B con velocità v2. In un istante successivo
t' le particelle si trovano in A' e B' con velocità v1' e
v2'.
Se indichiamo con m1 ed m2 le rispettive masse delle due particelle, la quantità di moto complessiva del sistema è
Nell'istante successivo t' avremo
Per il principio di conservazione della quantità di moto avremo:
Queste considerazioni portano alla seguente osservazione: un'interazione fra due particelle produce uno scambio di quantità di moto, cosicché la quantità di moto persa da una delle due particelle è uguale alla quantità di moto guadagnata dall'altra particella.
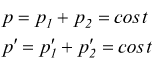sottraendo
membro a membro
cioè 
quindi:
notando
che
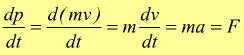
La forza è uguale alla derivata rispetto al tempo della quantità di moto (secondo principio della dinamica)
differenziando rispetto al tempo t: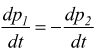 
l'equazione
precedente diventa:
Quando due particelle interagiscono , la forza agente su una particella è uguale ed opposta alla forza agente sull'altra (che poi coincide col terzo principio della dinamica).