Energia potenziale

L'energia potenziale è l'energia associata alla posizione di un oggetto o alla configurazione di un sistema. Si tratta di un tipo di energia che un oggetto ha in base alla sua posizione rispetto ad altri oggetti o rispetto a un punto di riferimento.

L'energia potenziale può essere convertita in energia cinetica quando l'oggetto si muove o cambia posizione. Alcuni esempi di energia potenziale sono l'energia gravitazionale, l'energia elastica e l'energia chimica.

Forze conservative

L'energia potenziale può essere associata soltanto ad una determinata tipologia di forze chiamate forze conservative.

Una forza è conservativa se il lavoro che essa fa nello spostamento dal punto iniziale a quello finale dipende solo dalle coordinate di questi due estremi e non dal particolare percorso eseguito nello spostamento.

In particolare il lavoro espresso da una forza conservativa lungo un percorso chiuso è nulla.

In meccanica, tipici esempi di forze conservative sono la gravità e l'energia elastica della molla.

Gravità

Per considerare questi casi dobbiamo ricordare che il lavoro viene espresso dalla formula

dove θ è l'angolo formato tra la direzione del vettore F e quella del vettore spostamento s.

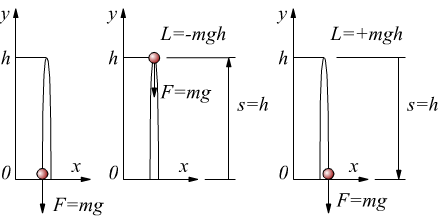
Nel disegno si vede una massa su cui agisce la forza peso dovuta alla gravitazie della terra F=mg.

Supponiamo che una forza esterna sia in grado di lanciare la massa verso l'alto con velocità iniziale v_o diretta verticalmente e quindi dotandola di energia cinetica

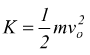
Mentre la massa sale, la terra compie lavoro su di essa fino ad arrestarla all'altezza y=h. il lavoro svolto dalla forza gravitazionale della Terra F=mg per andare da y=0 ad y=h vale L=F·s·cosθ=mg·h·cosθ ma dal disegno si vede che il vettore spostamento s è ruotato di 180° rispetto ad F=mg, quindi cos180°=-1. Risulta dunque che il lavoro fatto dalla forza gravitazionale per portare la massa da y=0÷h è L=-mgh.
Nel tratto di discesa si vede che sia la forza peso F=mg che il vettore spostamento hanno la stessa direzione, dunque θ=0 → cosθ=1. Risulta dunque che per il tratto di discesa che va da y=h÷0 il lavoro fatto dalla forza gravitazionale vale L=+mgh.

Il lavoro totale compiuto dalla Terra per il percorso completo della massa di andata e ritorno, è nullo; si conclude che la forza di gravità è una forza di tipo conservativo.

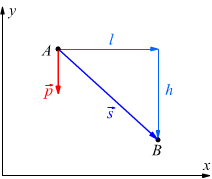
Supponiamo che un corpo di massa m e di forza peso p=mg si debba spostare da un punto di partenza A fino ad un punto di arrivo B, dobbiamo tener conto che il vettore forza peso p è sempre diretto verso il basso, quindi se eseguiamo il prodotto scalare

sia p che h hanno segno negativo perchè diretti in senso contrario alla direzione positiva degli assi y ed x (rispettivamente) del sistema di riferimento cartesiano.

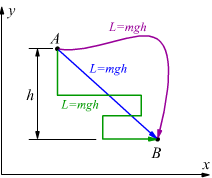
Si può dimostrare che scegliendo arbitrariamente la posizione di A e B si arriva sempre allo stesso risultato L=mgh con h=Δy differenza tra l'altezza di A e quella di B, questo indipendentemente dal percorso scelto.

Il fatto che il lavoro svolto dipenda esclusivamente dalla posizione iniziale e finale e non dal percorso eseguito permette di definire la forza peso come una forza di tipo conservativo dato che il lavoro che compie nello spostamento dal punto iniziale a quello finale dipende solo dalle coordinate di questi due estremi e non dal particolare percorso eseguito nello spostamento.

Forza elastica di una molla

Il lavoro espresso da una molla si calcola con lo stesso metodo. Supponiamo di valutare il lavoro che fa la forza di richiamo di una molla, precedentemente allungata, per spostare una massa su un piano privo di attrito, come si vede nello schema sotto:

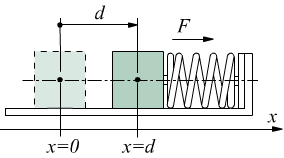
La forza della molla vale F=k·s, quindi il suo modulo non è costante come nel caso della forza gravitazionale ma dipende dalla coordinata x indicata. Formalmente, usando l'analisi matematica, per trovare il lavoro svolto dalla molla, dovremmo eseguire l'integrale di F·ds=F·dx considerando cosθ=cos0°=1 si avrebbe

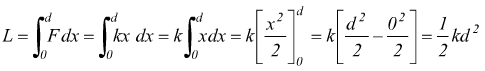
alla stessa conclusione si arriverebbe tramite constatazioni geometriche considerando sul piano F-x il prodotto k·x è rappresentato da una retta inclinata con coefficiente angolare k. Se la forza fosse costante F=k si avrebbe semplicemente L=kd che rappresenterebbe l'area sottesa alla linea di funzione F=k. Ma se la forza vale F=kx l'area sottesa alla

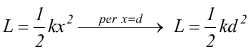
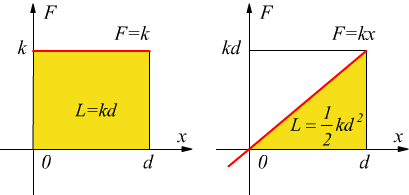
Ricordiamoci che l'area di un triangolo è base per altezza diviso 2, e quello che si vede nel disegno è un triangolo con base d ed altezza kd.

Constatare che la forza elastica è una forza di tipo conservativo richiede un attimo di attenzione. Nel disegno si vede un blocco di massa m agganciato ad una molla di costante elastica k. Il blocco può scorrere senza attrito sul piano orizzontale.

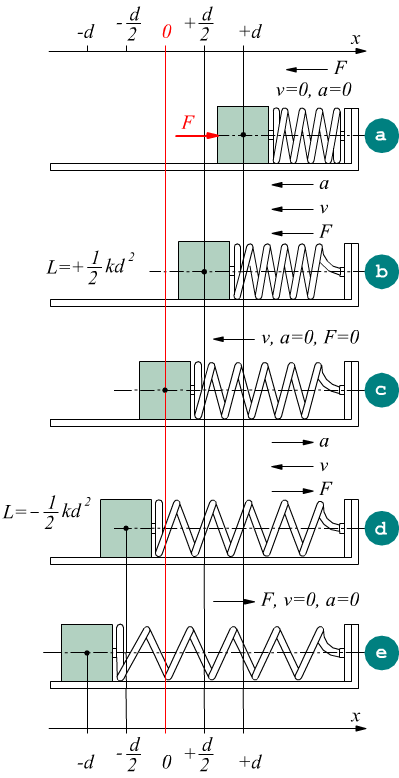
Inizialmente in a una forza esterna F comprime la molla e la massa ad essa agganciata. Di fatto, la molla immagazzina la forza F, perché per il terzo principio della dinamica per tenere in quiete il sistema deve esprimere una forza uguale ed opposta (ecco come fanno a funzionare i vecchi orologi analogici privi di energia elettrica e batterie al litio). Quando la forza esterna F (in rosso) viene tolta il sistema evolve accelerando verso sinistra b eseguendo uno spostamento verso il punto x=0 che noi ipotizziamo il punto di riposo della molla stessa; in questa fase la molla esegue un lavoro positivo

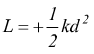
perchè forza e spostamento (che ha la stessa direzione del vettore velocità) hanno lo stesso verso.

Nel punto di riposo x=0 che si vede in c la forza F=0 e la massa ha smesso di accelerare (a=0) ma la massa è dotata di una velocità v non nulla.
Qui non si ha produzione di lavoro perché F=0.

Nella fase d la molla si sposta ancora verso sinistra con velocità decrescente perchè la molla è soggetta ad una forza di richiamo che fa decelerare la massa. In questa fase lo spostamento ha verso contrario rispetto al verso della forza della molla (ricordiamo che il verso dello spostamento coincide con quello della velocità) quindi cosθ=-1 e il lavoro espresso in questa fase vale

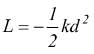
Alla fine si arriva nel punto e dove è massima la forza di richiamo F ma lo spostamento è nullo (come la velocità) quindi L=0.

Poi bisogna tornare al punto di origine. Sotto l'effetto del della forza F si ha la fase f qui spostamento (e velocità) hanno lo stesso verso della forza con cosθ=cos0°=1 quindi il lavoro in questa fase è positivo

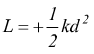
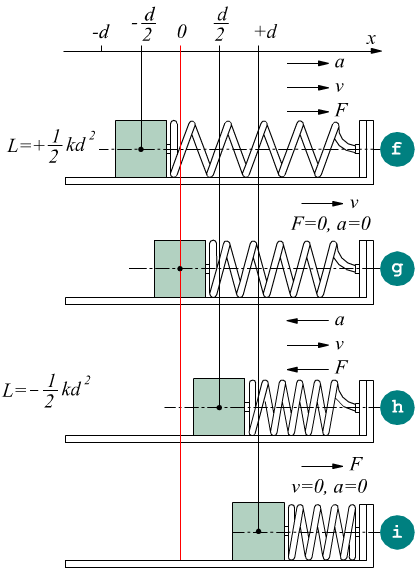
Nella fase g attraversiamo il punto di riposo della molla dove si ha F=0 → L=0. Nella fase h la molla torna a comprimersi e quindi il verso della forza e dello spostamento (coincidente con quello della velocità) sono contrari, producendo un lavoro negativo

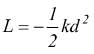
Nella fase i siamo tornati al punto iniziale e non si ha ne spostamento ne espressione di lavoro L=F·s=F·0=0.

Come si vede per eseguire un singolo ciclo (per tornare al punto di partenza) la molla ha compiuto per due volte un lavoro positivo e per due volte un lavoro negativo complessivamente il lavoro espresso da parte della molla è nullo. Se non ci fossero attriti (compreso quello dell'aria) questo sistema continuerebbe ad oscillare indefinitivamente (oscillatore armonico).
Si conclude che la forza elastica della molla è una forza di tipo conservativo.

Attrito

Un disco di massa M fissato all'estremità di un asticella rigida di lunghezza R che gli consente di ruotare attorno all'altra estremità della particella Come si vede nel disegno una forza esterna imprime una velocità iniziale v_o al disco costringendolo a ruotare lungo una circonferenza di raggio r su un piano orizzontale che esercita un attrito sul disco.

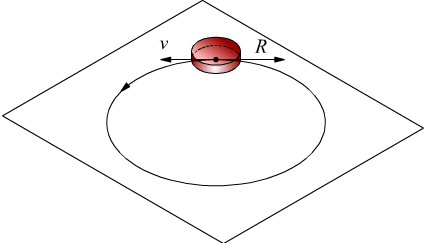
Venuta a cessare la forza esterna l'unica forza che compie lavoro sul disco rimane quella di attrito esercitata dalla superficie sulla faccia inferiore del disco. Essa agisce nella stessa direzione e in verso opposto a quello del movimento del disco (e quindi in senso opposto ai vettori velocità e spostamento) in modo che lavoro svolto dalla forza di attrito è sempre negativo. Pertanto quando il disco avrà effettuato un giro e sarà tornato nella stessa posizione di partenza il lavoro svolto su di esso dalla forza di attrito non è sicuramente nullo; sarà sempre, di certo, un valore negativo finito. Si conclude che la forza di attrito non è una forza conservativa. La forza di attrito viene per questo motivo definita come una forza dissipativa.

Energia potenziale

L'energia potenziale si può definire solo per le forze conservative. La variazione di energia potenziale di un sistema che trovandosi nella condizione A si porta nella condizione B ΔU=U_B-U_A viene definita come l'opposto del lavoro effettuato dalla forza conservativa per portare un sistema fisico dallo stato A allo stato B:

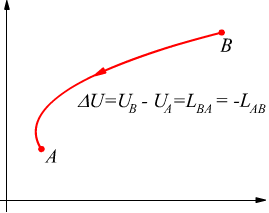
Scelta arbitrariamente una condizione di potenziale zero U_o=0 si può definire l'energia potenziale del punto A .

Per le forze dissipative, come l'attrito, questa legge non è valida, perchè il valore di questa energia sarebbe diverso per ogni possibile percorso diverso.

Possono, quindi, essere definite l'energia potenziale gravitazionale:

e l'energia potenziale elastica

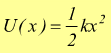
in entrambi i casi si vede come questa energia sia funzione di coordinate spaziali. Usando una definizione molto informale, possiamo dire, che l'energia potenziale può essere introdotta in sistema di oggetti che esercitano forze l'uno sull'altro.