Pendolo semplice
Il pendolo semplice è definito come una particella di massa m, sospesa ad un punto O ad un filo inestensibile di lunghezza l e di massa trascurabile
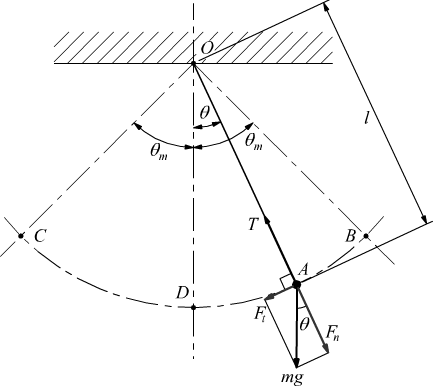
In condizione di equilibrio statico il corpo occupa la posizione D,in
modo che il proprio baricentro si trovi sulla retta verticale passante
per il punto di sospensione O.
Scostando il corpo puntiforme dalla sua posizione di equilibrio, fino
a portarlo al punto B, esso tende a tornare in D, ma per inerzia non
si ferma in quel punto, bensì prosegue fino alla posizione C,simmetrica
al punto B di partenza.
Poi, invertito il moto, ritornerà in B compiendo una serie di oscillazioni
che se si trascurano le resistenze passive saranno tutte uguali e continueranno
indefinitivamente nel tempo.
La presenza delle resistenze passive altera in realtà lo stato di cose
appena descritte: le oscillazioni diverranno sempre meno ampie (oscillazioni
smorzate) e pian piano il pendolo ritornerà nella sua condizione di
equilibrio in D.
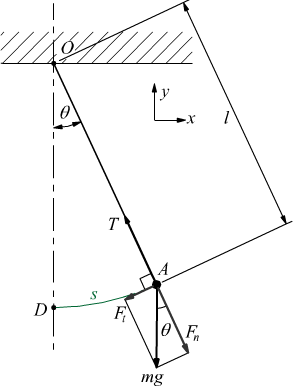
Identificando con s l'arco di circonferenza AD cerchiamo adesso, di studiare il moto della massa m tenendo conto del sistema di riferimento cartesiano adottato.
![]()
![]()
![]()
La componente Fn si elide col tiro T del filo che abbiamo detto è indeformabile. La componente Ft produce il moto del corpo verso la sua posizione di equilibrio ma la sua intensità in funzione del seno dell'angolo decresce fino ad annullarsi nel punto D in cui θ=0. Per la seconda legge della dinamica
![]() ma
se un moto si svolge lungo una traiettoria circolare di raggio R si
avrebbe
ma
se un moto si svolge lungo una traiettoria circolare di raggio R si
avrebbe
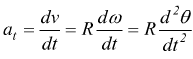 perchè
perchè 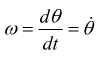 con
ω: velocità angolare
con
ω: velocità angolare
nel nostro caso R=l=lunghezza del filo
![]()
![]()
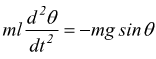
quindi l'equazione del moto è 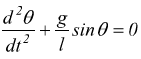
dunque bisogna risolvere l'equazione differenziale omogenea di secondo grado a coefficienti costanti che se manteniamo in questa forma è molto laboriosa da risolvere e porta a considerare degli integrali ellittici. Limitiamoci allora a valutare questa relazione solo per le piccole oscillazioni ( 10°< ) ponendo
![]() con
con
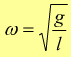
quest'ultima è completamente analoga all'equazione del moto armonico che ha soluzione
![]() a
a
con θm e ɸ costanti di integrazione dipendenti dalle condizioni iniziali.

L'analogia si deduce dal fatto che per piccole oscillazioni
![]() con
con
![]() b
b
La a e la b sono proporzionali per mezzo del fattore di scala l (lunghezza del pendolo).
Il periodo del pendolo semplice risulta, dunque, essere:
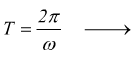
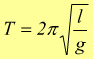
Si vede che il periodo è indipendente dalla massa del pendolo e dall'ampiezza delle oscillazioni.
: angolo 45°
: lunghezza 100 px
: smorzamento 0
Pendolo composto
Supponiamo di vincolare parzialmente un corpo di forma qualsiasi,ponendo una cerniera (O) in un punto diverso dal suo baricentro
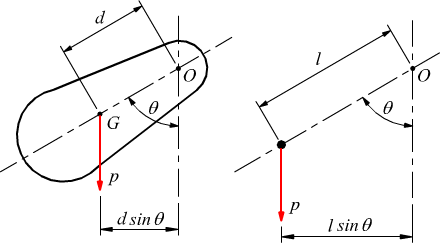
il corpo soggetto esclusivamente al peso proprio, è in equilibrio solo
quando la retta d'azione del peso passa per la cerniera O.
Se viene spostato da tale posizione, inizia una serie di oscillazioni,esattamente
come un pendolo.
E' chiaro però che ad esso non possono essere applicate le leggi del pendolo, ricavate nel caso precedente del pendolo semplice, a causa della diversa distribuzione dei pesi parziali. Un sistema oscillante come quello descritto viene solitamente chiamato pendolo composto.
Lo studio dinamico di un pendolo composto è notevolmente semplificato,
se si ricorre all'artificio di ricondurre il suo moto a quello di un
pendolo semplice di lunghezza l (lunghezza ridotta).
Il corpo rigido costituente il pendolo composto è soggetto ad un momento
![]() Applicando la seconda legge della dinamica per un
corpo rigido in rotazione
Applicando la seconda legge della dinamica per un
corpo rigido in rotazione ![]()
con J : momento di inerzia del corpo rigido rispetto all'asse di rotazione ed α : accelerazione angolare; si ha
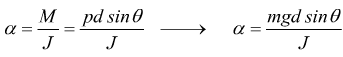
J può essere ottenuto dal momento di inerzia baricentrico JG con la formula di trasposizione
![]() con
con
![]()
con ρ : raggio di inerzia rispetto al baricentro del corpo; ne consegue
![]() con
con
![]() raggio giratore ; si
ha in definitiva
raggio giratore ; si
ha in definitiva
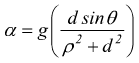
Invece, il pendolo semplice equivalente, è soggetto ad un momento
![]() per
questo
per
questo ![]() dunque
dunque
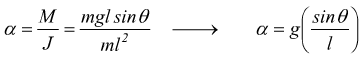
dato che per i due pendoli devono valere le stesse regole dinamiche, le accelerazioni angolari α devono essere uguali
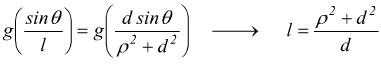 Il
periodo delle oscillazioni sarà dunque
Il
periodo delle oscillazioni sarà dunque
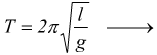
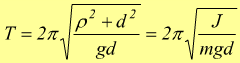
Si nota come il periodo del pendolo composto sia indipendente dalla
sua massa e dalla sua forma geometrica.
Alle stesse conclusioni si potrebbe arrivare inquadrando il sistema
nel sistema di coordinate già usando in precedenza
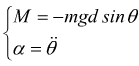 usando
l'equazione
usando
l'equazione ![]()
sempre usando l'approssimazione sinθ∼θ

essendo ![]() diventa
diventa  risolvendo in modo analogo alll'equazione precedente si avrebbe
risolvendo in modo analogo alll'equazione precedente si avrebbe
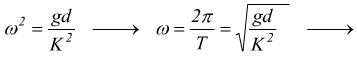
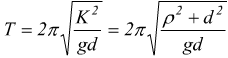
 edutecnica
edutecnica