Interferenza di onde
Due onde sinusoidali sulla stessa corda presentano interferenza, sommandosi
o sottraendosi secondo il principio di sovrapposizione degli effetti.
Se le due onde viaggiano nella stessa direzione e hanno la stessa ampiezza
ym e la stessa frequenza (e quindi la stessa lunghezza d’onda), ma differiscono
in fase di un angolo di fase ϕ, il risultato è una singola onda con
questa stessa frequenza.

Se ϕ=0 le onde sono in fase e la loro interferenza è completamente costruttiva; se ϕ=π esse si trovano in opposizione di fase e la loro interferenza è completamente distruttiva.
E' possibile dimostrare la relazione sopra indicata ipotizzando che le due onde siano descritte dalle due seguenti equazioni.
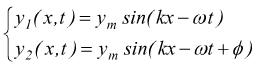 1
1
Ipotizziamo che queste due onde percorrano la stessa corda con la stessa pulsazione ω (e quindi la stessa frequenza), lo stesso numero d'onda angolare k (e quindi la stessa lunghezza d'onda e la stessa ampiezza ym. Per il principio di sovrapposizione, l'onda risultante dalla sovrapposizione sarà
![]() 2
2
dunque
![]() 3
3
per le formule di addizione e sottrazione sappiamo che
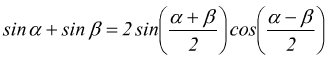
applicando quest'ultima regola alla formula 3 otteniamo:
 4
4
l'onda risultante è quindi anch'essa sinusoidale, in moto nel verso positivo delle x, ed è l'unica onda che vediamo effettivamente propagarsi lungo la corda (non si vedono materialmente le due onde separate delle equazioni 1.
Quando due onde sinusoidali aventi stessa ampiezza e lunghezza d'onda si muovono concordemente nella stessa direzione lungo una corda tesa, interferiscono a formare un'onda risultante sinusoidale che si propaga sempre nella medesima direzione.
L'onda risultante differisce dalle onde componenti soltanto per due aspetti: l'angolo di fase, che è $ϕ/2$, e la sua ampiezza, che è stata evidenziata nella formula 4.
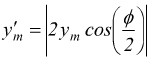 5
5
Se ϕ= 0 rad (ovvero 0°) le due onde sono esattamente in fase la 4 si riduce a:
![]() 6
6
Le due onde sono mostrate nello schema seguente e l'onda risultante è riportata
sul grafico a.
In questo caso le due onde sono esattamente in fase e producono un'onda
più ampia riportata in d.

Notiamo sia dalla figura sia dall'equazione 6
che l'ampiezza dell'onda risultante è il doppio di quella delle onde interferenti.
Questa è la massima ampiezza che l'onda risultante può avere, perché il
coseno delle equazioni 5 e 6
presenta il suo massimo valore per ϕ= 0.
L'interferenza in questo caso è completamente costruttiva. Se ϕ= π
rad (ovvero 180°), le due onde sono completamente fuori fase indicata in
(b). Il fattore $cos(ϕ/2)$ diventa $cos(π/2) = 0$ e l'ampiezza dell'onda
risultante (eq. 5) è zero. Abbiamo, quindi,
per tutti i valori di x e t :
$y'(x,t)=0$ (con ϕ=π rad) 7
L'onda risultante è riportata sul grafico e.
Si noti che, malgrado l'invio di due onde lungo la corda, non si verifica
alcun moto della corda. Questo tipo di interferenza è chiamata completamente
distruttiva. Dato che un'onda sinusoidale si ripete ogni 2π rad, una
differenza di ϕ = 2n rad (360°) corrisponde a una traslazione di un'onda
rispetto all'altra di una lunghezza d'onda esatta. La differenza di fase
si può quindi esprimere anche in termini di lunghezze d'onda.
Per esempio nella figura b le onde sono sfasate
di mezza lunghezza d'onda.
Nella tabella seguente riportiamo alcuni altri esempi di sfasamenti e dell'interferenza
che producono.
| differenza di fase | ampiezza onda risultante | tipo di interferenza | ||
| gradi | radianti | lung.d’onda | ||
| 0 | 0 | 0 | 2ym | tot.costruttiva |
| 120 | 2/3π | 0,33 | ym | intermedia |
| 180 | π | 0,50 | 0 | tot.distruttiva |
| 240 | 4/3π | 0,67 | ym | intermedia |
| 360 | 2π | 1 | 2ym | tot.costruttiva |
Quando l'interferenza non è né completamente costruttiva né completamente
distruttiva, l'ampiezza dell'onda risultante presenta valori intermedi tra
0 e 2ym.
Per esempio dalla tabella osserviamo che per due onde sfasate di 120° (
$ϕ= {2π}/3$ rad = 0,33 lunghezze d'onda), l'onda risultante ha un'ampiezza
pari a ym, la stessa delle onde interferenti fig. c
e fig. f.
Il risultato non cambierebbe se volessimo studiare l'interferenza tra le due onde in termini della funzione coseno.

quindi
![]()
per le formule di prostaferesi
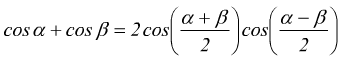
applicando questa formula a quella immediatamente precedente:

abbiamo sempre una funzione sinusoidale con ampiezza pari alla formula 5.
In questa pagina è presente una piccola applicazione interattiva sull'interferenza di onde progressive.
 edutecnica
edutecnica