Energia e potenza di un’onda

    

Quando inviamo un'onda lungo una corda tesa, forniamo energia per muovere la corda. L'onda si propagandosi lungo la corda tesa, trasporta questa energia sia come energia cinetica sia come energia potenziale. Consideriamo le seguenti osservazioni per queste due cose.

Energia cinetica

    

Un elemento della corda di massa dm, oscillante trasversalmente con moto armonico semplice mentre l'onda lo attraversa; avrà certamente un’ energia cinetica associata alla sua velocità trasversale u. Quando l'elemento passa velocemente attraverso la sua posizione y = 0 (elemento b nel disegno seguente

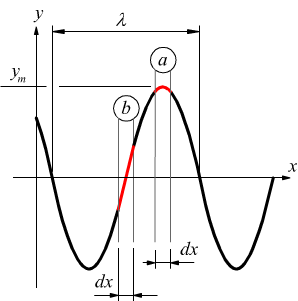
la sua velocità trasversale e di conseguenza la sua energia cinetica è massima. Quando l'elemento si trova nella sua posizione estrema (elemento a) in cui y=y_m. La sua velocità trasversale e di conseguenza la sua energia cinetica sarà zero.

Energia potenziale elastica

    

Per trasmettere un'onda sinusoidale lungo una corda tesa, l'onda deve necessariamente tendere ancor più la corda. Quando un elemento della corda di lunghezza dx oscilla trasversalmente, la sua lunghezza deve crescere e decrescere con un andamento periodico per permettere all'elemento della corda di adattarsi alla forma sinusoidale dell'onda. L'energia potenziale è associata a questi cambiamenti di lunghezza, come se si trattasse di una molla. Quando l'elemento della corda è nella sua posizione y=y_m (elemento a del disegno precedente), la sua lunghezza ha il valore normale dx, quindi l'energia potenziale immagazzinata è zero. Invece, quando l'elemento passa velocemente nella sua posizione y=0 (elemento b), l’elemento, viene teso al massimo e l'energia potenziale immagazzinata raggiunge conseguentemente il suo valore massimo.

Trasferimento di energia

    

L'elemento oscillante della corda ha quindi energia cinetica ed energia potenziale massime in corrispondenza di y=0. Nella situazione istantanea del disegno precedente, i tratti della corda corrispondenti al massimo spostamento hanno energia nulla, mentre i tratti in cui lo spostamento è nullo posseggono la massima energia. Durante la propagazione, la tensione nella corda compie continuamente lavoro per trasferire energia dai tratti che ne sono dotati a quelli che ne sono privi. Immaginiamo di voler instaurare un'onda su una corda tesa lungo l'asse x, il cui spostamento sia descritto dall'equazione : $$y(x,t)=y_m sin(kx-ωt)$$ Possiamo farlo, facendo oscillare alternativamente un'estremità della corda, come nella figura seguente.

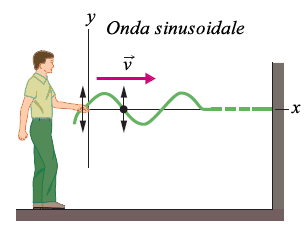
In questo modo forniamo continuamente energia per imprimere il moto alla corda e per tenderne la struttura; di conseguenza gli elementi della corda, che oscillano perpendicolarmente all'asse x, sono dotati di energia cinetica e di energia potenziale. Man mano che l'onda si muove passando da un elemento al successivo, precedentemente a riposo, l'energia viene trasferita al nuovo elemento. Pertanto, si può affermare che l'onda trasferisce energia lungo la corda.

Potenza trasferita

    

Chiamiamo dK una quantità di energia cinetica arbitrariamente piccola associata a un elemento infinitesimo di corda dm che oscilla con velocità trasversale u.

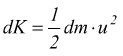      1

Per trovare il valore di u, deriviamo l'equazione $y(x,t)=y_m sin(kx-ωt)$ rispetto al tempo mantenendo x costante:

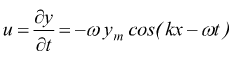    2

Se μ è la massa lineica della corda, risulta dm = μdx. Usiamo allora questa relazione riscrivendo l'equazione X come:

     3

Dividendo l'equazione 3 per dt otteniamo il rapporto temporale con cui varia l'energia cinetica di un elemento di corda e quindi la velocità con cui l'energia cinetica viene trasportata dall'onda. Il rapporto dx/dt che otteniamo a destra nell'equazione 3 è la velocità longitudinale v (in direzione positiva dell'asse x), e quindi abbiamo:

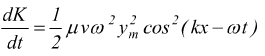    4

Il valor medio di questo rapporto è

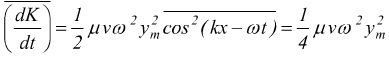    5

Nell'equazione 5 abbiamo operato la media su un numero intero di lunghezze d'onda e abbiamo sfruttato il fatto che il valore medio del quadrato di una funzione coseno su un numero intero di lunghezze d'onda è 1/2. Anche l'energia potenziale elastica è trasportata dall'onda alla stessa velocità media, descritta dall'equazione 5.
E' possibile dimostrare che, in un sistema oscillante come un pendolo o un sistema a molla, l'energia cinetica media e l'energia potenziale media sono uguali. La potenza media, che esprime la "rapidità" media alla quale entrambe le energie di cui sopra sono trasmesse dall'onda, è quindi :

   6

oppure, per l'equazione 5

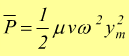    potenza media.