Strutture iperstatiche
Nelle strutture isostatiche, il numero dei gradi di libertà è pari ai gradi di vincolo, le sole equazioni della statica sono sufficienti per determinare le reazioni vincolari e di conseguenza tutti i diagrammi degli sforzi. Se il numero dei vincoli (incogniti) è tale da superare le equazioni di cui disponiamo la struttura viene definita iperstatica. Come è noto, se in un problema il numero di incognite supera il numero di equazioni a disposizione, il problema è irrisolvibile. Il caso delle strutture iperstatiche, necessita dunque, un particolare tipo di approccio.
Facciamo l'esempio più semplice: la trave a mensola incastrata ad un estremo. Per una trave semplicemente incastrata ad un estremo, le reazioni vincolari sono 3 come i suoi gradi di libertà; se a questa configurazione aggiungiamo un appoggio all'estremo libero, la struttura acquista un ulteriore grado di vincolo. Nel problema ci sono 4 incognite, ma noi disponiamo solo delle 3 equazioni della statica.
Sostituiamo il vincolo in B con la rispettiva reazione: la forza Y introdotta da quel tipo di vincolo
La prima equazione identifica la reazione Ax.
Poi, rimaniamo con due equazioni, e tre incognite MA Y e By
(sistema irrisolvibile).
Questa situazione può essere superata ricorrendo alla nozione di deformabilità di un corpo solido. Sappiamo che le strutture isostatiche sono considerate per definizione rigide, le strutture iperstatiche , invece, devono essere considerate deformabili.
Usiamo il principio di sovrapposizione degli effetti applicato alle deformazioni del vincolo superfluo che noi (arbitrariamente) riteniamo sia l'appoggio in B.
Immaginiamo di liberare la trave del solo vincolo di appoggio
si ottiene in tal caso una struttura isostatica soggetta solo alla forza F . La configurazione è riconducibile allo schema 2 del prontuario, dove, per lo spostamento f dell'estremo libero si ha
Se poi togliamo il carico F per considerare solo la forza Y che sostituisce il vincolo (schema 1 del prontuario) lo spostamento dell'estremo libero sarà
avendo i due spostamenti verso contrario deve essere
sostituendo nel sistema
dalla prima si ottiene la reazione vincolare 
dalla seconda si ottiene 
.
Passiamo a considerare la sollecitazione al taglio.
Valutiamo il momento flettente
in per x=l/2 si ha
dalle suddette relazioni si ricava il diagramma del momento flettente
Strutture più volte iperstatiche
Il caso più frequente è trave doppiamente incastrata, in questo caso con un carico concentrato sulla mezzeria :3 gradi di libertà, 6 reazioni vincolari. Sostituiamo la struttura iperstatica con quella isostatica più semplice
Il carrello ha due gradi di libertà e dunque verrà assoggettato due azioni esterne (fittizie) supplementari:l'azione assiale X ed il momento W. La cerniera ha un grado di libertà e verrà caricata da un momento esterno Z.
In questo nuovo schema, F,W,Z,X sono da interpretare come azioni esterne.
Se ipotizziamo la struttura soggetta solo alla forza F, facendo riferimento
allo schema 11
del prontuario:
mentre se agissero solo i momenti W e Z
dallo schema 30 si avrebbe
dato che la trave è incastrata agli estremi le rotazioni delle sezioni terminali devono essere nulle, quindi α=φ e β=φ
dalla seconda eq. si ha 
sostituendo
nella prima
tornando alla precedente si trova 
.
Tenendo conto che per la struttura completa, lungo l'asse y si avrebbe per le reazioni vincolari Ay e By:
e non essendoci forze attive orizzontali è X=Bx=0. E' possibile ora tracciare il diagramma del taglio
Quando facciamo il diagramma del momento dobbiamo tenere conto che MA=W=Fl/8 tenendo conto della relazione
Lo stesso discorso potrebbe riguardare la trave doppiamente incastrata con carico uniforme
dove i due momenti sono indicati identici per ragioni di simmetria
Dallo schema 12 la rotazione agli estremi per una trave isostatica uniformemente caricata è
mentre
come nel caso precedente se ipotizziamo agenti solo i due momenti Z si ha 
(schema 30 con MA=MB) quindi
Le reazioni verticali sono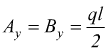 
per
il taglio avremo
Mentre per il momento flettente è
trovando
