Esercizio 30

Due onde sinusoidali di ugual frequenza avanzano concordi lungo la medesima corda tesa. Trovare l'ampiezza dell'onda risultante sapendo che $y_{m1}=3cm$, $y_{m2}=4cm$, $ϕ_1=0$ e $ϕ_2=π/2$ rad.

Soluzione

Questo esercizio contempla la presenza di due onde sinusoidali di diversa ampiezza ma che hanno comunque la stessa frequenza e quindi la stessa pulsazione e lo stesso numero d’onda angolare k. In questo caso è consigliabile un approccio che proviene dall’elettrotecnica normalmente indicato come metodo dei fasori. Ogni singola onda viene considerata un vettore di fase anche chiamato fasore rotante; si tratta di un vettore che ruota attorno al suo punto di applicazione collocato all'origine del sistema di coordinate. La velocità angolare del vettore è pari a ω mentre il suo modulo è pari ad $y_m$. Possiamo sommare le due onde:

$y_1(x,t)=y_{m1}sin(kx-ωt)$
$y_2(x,t)=y_{m2}sin(kx-ωt+ϕ)$
ottenendo un’onda risultante
$y’(x,t)=y’_m sin(kx-ω+γ)$

sommando vettorialmente sul piano di Gauss i vettori rappresentativi delle due onde considerandone il modulo e la fase.

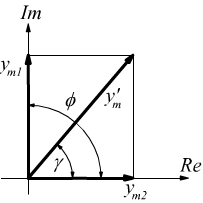
Per il teorema di Pitagora il vettore risultante avrà modulo
$y’_m=√{y_{m1}^2+ y_{m2}^2}=5 cm$
poi avremo

$y’=y_1+y_2=3sin(kx-ωt)+ 4sin(kx-ωt+ϕ)$
ma

$sin(kx-ωt+π/2)=cos(kx-&ωt) $
dunque

$$y’=5[{3/5}sin(kx-ωt)+{4/5}cos(kx-ωt)]$$
$y’=5sin(kx-ωt+γ)$

La fase γ si può ricavare con la trigonometria:

$$γ=arctg(y_{m1}/ y_{m2})= arctg(4/3)=53°$$