Esercizio 17
Un’onda sinusoidale trasversale di lunghezza d’onda 20cm si muove lungo una corda nel verso positivo delle x. Lo spostamento dalla posizione di equilibrio di una particella in x=0 in funzione del tempo è riportato nel seguente disegno
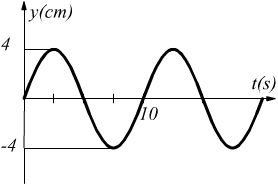
Trovare il valore massimo ym il numero d’onda k la pulsazione ω, la costante di fase ϕ il segno del fattore ωt nell’quazione d’onda, la velocità dell’onda. Trovare inoltre la velocità trasversale nel punto x=0 all’istante t=5 s.
Soluzione
Dal disegno si vede che è ym=4cm. Il numero d’onda viene ottenuto come
$$k={2π}/λ=π/10=0,31 {rad}/{cm}$$
La pulsazione ω può essere espressa come:
$$ω={2π}/T=π/5=0,63 {rad}/s$$
Nel testo dell’esercizio viene specificato che l’onda è progressiva nel senso positivo dell’asse x, quidi il segno del termine ωt deve essere negativo.
Dunque l’equazione generale della forma d’onda descritta deve essere:
$$y(x,t)=y_m sin(kx-ωt+ϕ)$$
dunque per x=0 dovrà essere
$$y(0,t)=y_m sin(-ωt+ϕ)$$
ma comunque si tratta di una funzione sinusoidale positiva, sapendo che $sin(x)=sin(π-x)$ sarà $sin(-ωt+ϕ)=sin(ωt)$ dunque deve necessariamente essere ϕ=π per t=0 avremo allora:
$$y(0,t)=y_m sin(kx+π)=-y_m sin(kx)$$
funzione sinusoidale negativa.
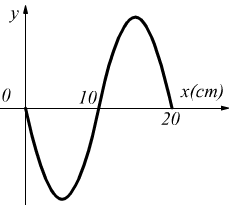
La velocità dell’onda può essere facilmente trovata sapendo che
$$f=1/T=1/10=0,1 Hz$$
poi $v=λf=20·0,1=2 {cm}/s$.
L’equazione generale dell’onda è dunque esprimibile come
$$y(x,t)= 4sin({πx}/10-{πt}/5+π)=-4sin({πx}/10-{πt}/5)$$
derivando rispetto al tempo avremo
$$u(x,t)={∂y}/{∂t}=4(π/t)cos({πx}/10-{πt}/5)$$
che fornisce la soluzione $u(0,5)=-2,5 {cm}/s$