Esercizio 1

Un’onda sull’acqua ha la forma di un’onda armonica con ampiezza 2m e lunghezza d’onda 5m qual’è l’altezza dell’onda a 70 cm a destra del picco dell’onda.

Soluzione

Usando la formula

$$y(x,t)=y_m cos{(ωt-{{2π}/λ}x)}$$

Assumendo di effettuare la misurazione al tempo t=0,a 70 cm a destra dell’onda ( secondo la direzione positiva di x ) si ha

$$y(x,t)=y_m cos{(-{{2π}/λ}x)}=y_m cos{({{2π}/λ}x)}$$

$$y(x)=2 cos{(-{{2π}/4}0,7)}=1,27 m $$

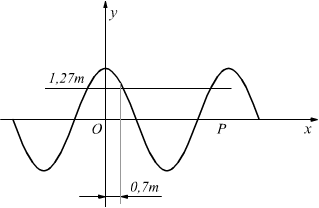
potevamo anche usare la funzione seno e in tal caso:

$$y(x,t)=y_m sin{(kx-ωt)}$$

per t=0

$$y(x)=y_m sin{({{2π}/λ}x)}$$

in tal caso $x_m={λ/4}={5/4}=1,25 m$ è il punto in cui la funzione seno assume il massimo y_m=2m; allora x_p=1,25+0,7=1,95 m è il punto a destra di 0,7m dalla cresta dell’onda.

$$y_p=y_m sin{({{2π}/λ}x_p)}$$

$$y_p=2 sin{({{2π}/5}·1,95)}=1,27 m$$

Da questo esercizio si deduce che per studiare l’onda è possibile usare sia la funzione seno che la funzione coseno, indifferentemente.