Criteri di sicurezza dei materiali
Il calcolo strutturale degli elementi di una costruzione si prefigge lo scopo di garantirne la sicurezza di un organo meccanico nel corso del suo utilizzo; cioè, occorre garantire che non si verifichino deformazioni intollerabili o, persino, la rottura dell’organo stesso.
Una volta conosciute le caratteristiche di sforzo in corrispondenza della sezione più pericolosa di un corpo, si possono ottenere i valori delle tensioni in ogni punto , identificando i punti più sollecitati al fine di verificarne la resistenza.
La verifica di resistenza consiste nell’accertare che il valore della tensione interna massima $σ_ {max}$ sia inferiore ad una tensione limite di pericolo relativa allo sforzo, affinché l’organo in esame risulti in sicurezza.
Per tutti i materiali sottoposti alla semplice azione assiale si assume, come tensione limite, la tensione di rottura $R_m$ o la tensione di snervamento $R_s$.
Ciò nonostante nei calcoli di progetto o di verifica non si adotta mai come tensione limite il carico unitario di rottura $R_m$ o di snervamento $R_s$, perché se durante il funzionamento si arrivasse ad una sollecitazione pari ad una di esse, non si potrebbe escludere danni all’organo meccanico, sia pure con maggiore o minore probabilità, a seconda dei casi.
Carico unitario di sicurezza
Queste eventualità possono essere causate da difetti interni o esterni al materiale, difetti di esecuzione o di montaggio, carichi più gravosi del previsto nei calcoli.
Per queste ragioni è necessario basarsi su una frazione della tensione limite detta tensione ammissibile statica $σ_a$ o carico unitario di sicurezza.
Le considerazioni fatte per la valutazione della tensione ammissibile sono sufficientemente esatte per tutti gli elementi strutturali soggetti a carichi statici, ma quando gli organi meccanici sono soggetti a sollecitazioni variabili nel tempo, bisogna assicurarsi che le tensioni interne siano inferiori ad una nuova tensione limite, che viene definita limite di resistenza a fatica.
Tensione ammissibile statica
Introducendo un coefficiente numerico detto grado di sicurezza g, la tensione ammissibile $σ_a$ in condizione di sollecitazioni statiche si esprime come:
$$σ_a=R/g$$
Dove con R indichiamo (per il momento) indifferentemente $R_m$ o $R_s$ cioè la tensione limite.
Affinché per un elemento strutturale non si verifichino pericoli di cedimento, eccessive deformazioni o rottura, occorre che il valore massimo delle tensioni interne non superi il valore della tensione ammissibile.
Per tensioni normali statiche deve essere
$σ_ {max}≤σ_a$ (•)
Dove, come abbiamo detto, $σ_a$ è la tensione normale ammissibile.
Per sollecitazione a torsione, avremo per le tensioni tangenziali statiche:
$τ_ {max}≤τ_a$ (×)
In cui $τ_a$ prende il nome di tensione tangenziale ammissibile.
Il valore della tensione tangenziale ammissibile può essere espresso in funzione della tensione normale ammissibile tramite la relazione
$$τ_a=σ_a/√3=0,577σ_a$$Per materiali fragili che giungono a rottura con piccole deformazioni, il calcolo della tensione ammissibile si esegue facendo riferimento alla tensione di rottura $R_m$, mentre per materiali duttili, come acciai che giungono a rottura con notevole deformazione, non potendo ammettere eccessive deformazioni si può fare riferimento alla tensione di snervamento $R_s$. Indicativamente per materiali fragili avremo
$$σ_a=R_m/g_r$$
Per materiali duttili:
$$σ_a=R_s/g_s$$
Dato che al superamento della tensione di snervamento $R_s$, da parte della tensione agente nell’organo meccanico non corrisponde immediatamente un pericolo di grave danno, come invece accade superando il carico unitario di rottura $R_m$, si possono assumere per il grado di sicurezza $g_s$ valori inferiori a quelli di $g_r$ adottati nei confronti della tensione di rottura.
Le norme fissano i valori delle tensioni ammissibili e quindi implicitamente anche i gradi di sicurezza rispetto alla rottura e rispetto allo snervamento: per gli acciai di uso generale, appartenenti alle classi S235, S275, S355 i valori di $σ_a$ riportati nella seguente tabella:
|
Acciai laminati UNI EN 10027/1 |
Carico di rottura Rm (N/mm2) |
Carico di snervamento Rs (N/mm2) |
σa (N/mm2) | |
| Spessori t≤40mm |
Spessori t>40mm |
|||
| S235 (già Fe360) |
320÷510 | 175÷235 | 160 | 140 |
| S275 (già Fe430) |
380÷580 | 380÷275 | 190 | 170 |
| S355 (già Fe510) |
450÷680 | 275÷355 | 240 | 210 |
Grado di sicurezza
In base a quanto detto sulla nozione di tensione ammissibile, possiamo dare la seguente definizione di grado di sicurezza:
Il grado di sicurezza è il rapporto tra la tensione di rottura, o la tensione di snervamento e la tensione massima prevedibile nei punti più sollecitati di un elemento strutturale.
Nella scelta del grado di sicurezza si deve tener conto di diversi fattori, dovuti all’impossibilità di conoscere completamente l’effettivo stato di sollecitazione e le effettive caratteristiche di resistenza del materiale, oltre alle possibili differenze tra tensioni calcolate e tensioni reali.
Per i diversi materiali da costruzione, nelle condizioni ordinarie di temperatura e di ambiente, si possono assumere in linea di massima , nel caso di sollecitazioni statiche, i gradi di sicurezza riportati nella seguente tabella.
| Materiale | Stato | Sollecitazione a trazione | |
| gr | gs | ||
| Acciaio | Laminati, fucinati |
2,3÷3 | 1,5÷2 |
| Getti | 3,2÷4,2 | 1,8÷2,5 | |
| Ghisa | Getti | 7÷9 | - |
Verificate le sollecitazioni esterne nelle condizioni più sfavorevoli e scelti i materiali da impiegare, si effettuano i calcoli necessari per la verifica o il progetto del componente:
La verifica consiste nel determinare la tensione interna massima a cui è soggetto il materiale, verificando, mediamente la (•) o la (×) che essa sia inferiore al valore della tensione ammissibile.
Il progetto (dimensionamento) consiste nel determinare le dimensioni minime della sezione resistente dell’organo meccanico in esame, imponendo tramite la (•) o la (×) che la tensione interna massima del materiale non superi la tensione ammissibile.
ESEMPIO: Un tirante a sezione rettangolare, disegnato qui sotto, è costituito da acciaio S235 con carico unitario di rottura $R_m=360\;N/{mm^2}$ e da un carico unitario di snervamento $R_s=235\;N/{mm^2}$.
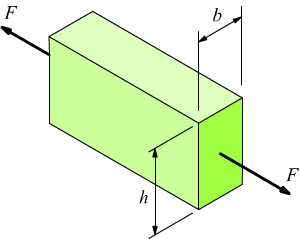
Sapendo che il tirante è sottoposto ad una trazione di una forza $F=10^5\;N$ e che le dimensioni della sua sezione trasversale sono b=12 mm ed h=100 mm, verificarne la sicurezza.
La sezione soggetta allo sforzo vale
$S=b⋅h=12⋅100=1200\;mm^2$
Lo sforzo a cui è soggetto l’elemento è
$$σ=F/A={10^5}/{1,2⋅10^3}=83,3\;N/{mm^2}$$
Assumendo un grado di sicurezza alla rottura $g_r=3$
$$σ_a=R_m/g_r=360/3=120\;N/{mm^2}$$
Assumendo un grado di sicurezza allo snervamento $g_s=2$
$$σ_a=R_s/g_s=235/2=117,5\;N/{mm^2}$$
In entrambi i casi si ha $σ<σ_a$ : la sicurezza dell’elemento è dunque garantita.
Resistenza a fatica
Difficilmente gli organi meccanici subiscono sforzi costanti nel tempo, Nella gran parte dei casi questi sforzi variano periodicamente, secondo cicli che continuano a ripetersi. In questo modo viene generato uno sforzo denominato sollecitazione a fatica.
Un materiale che subisce questo tipo di sforzo manifesta una resistenza minore di quella che avrebbe se fosse sottoposto a sollecitazioni statiche della stessa intensità massima.
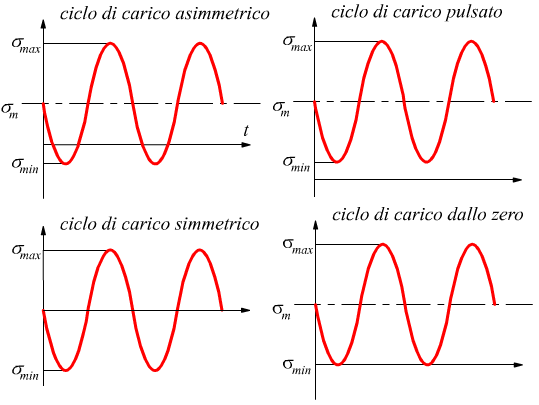
Le sollecitazioni a fatica possono essere di tipo alternato o di tipo pulsato a secondo del variare periodico delle forze.
In questo tipo di fenomeno oscillatorio si possono individuare alcuni parametri tipici che interessano la tensione esercitata sull’organo.
$$σ_h=1/2(σ_{max}-σ_{min})$$ ampiezza dell’oscillazione della tensione
$$σ_m=1/2(σ_{max}+σ_{min})$$ tensione media
Nei seguenti disegni sono riportate le caratteristiche principali delle tensioni alternate e pulsate che possono interessare un elemento meccanico.
La legge generale che mette in relazione il carico massimo ammissibile statico $σ_a$ con la tensione ammissibile dinamica a fatica $σ_d$ è la seguente
$$σ_d=σ_a(2/3+1/3 σ_{ min}/σ_{ min}) $$
In tal modo se $σ_ {max}=σ_ {min}$ la sollecitazione sarà di tipo statico ed avremo
$σ_d=σ_ a$
Per le sollecitazioni a fatica sono di tipo pulsato in cui $σ_ {min}=0$ avremo
$σ_d=2/3σ_ a$
Se le sollecitazioni a fatica sono di tipo alternato con $σ_{min}=-σ_ {max}$ la tensione dinamica ammissibile a fatica vale:
$σ_ d=1/3σ_ a$
NOTA: tutti gli esercizi svolti nel sito, per una questione di omogeneità, ottengono il carico unitario di sicurezza, cioè la tensione ammissibile statica dividendo il carico di rottura $R_m$ (che per semplicità viene scritto R) per un grado di sicurezza $g_r=3$.
I materiali vengono assegnati con la vecchia notazione (Fe360, Fe430, etc..) precedente alla UNI EN 10027-1,in modo da render subito disponibile il carico di rottura.
In presenza di sollecitazione a fatica la tensione ammissibile dinamica $σ_d$viene ottenuta con le considerazioni precedenti.
 edutecnica
edutecnica