Cinematica
Si dice che un oggetto è in moto rispetto ad un altro, quando la sua
posizione misurata rispetto ad un secondo corpo cambia nel tempo. Se questa
posizione non cambia l'oggetto è in quiete relativa. La quiete e il moto
sono concetti relativi.
Un corpo dotato di movimento è detto mobile; la linea percorsa da tale
corpo è detta traiettoria.
Si ha moto rettilineo quando la traiettoria
è una linea retta, si ha moto curvilineo
quando la traiettoria è una linea curva; quando la traiettoria è un cerchio
si ha il moto circolare rotatorio.
Si ha moto continuo quando il corpo mobile
si muove sempre nello stesso senso, si ha moto
alternativo quando il corpo mobile inverte successivamente il movimento.
Lo spazio è la lunghezza della traiettoria
percorsa dal corpo in movimento. Il tempo
è la durata del moto di un corpo. La velocità
è lo spazio percorso nell'unità di tempo. Se la velocità si mantiene costante
durante tutto il percorso si ha moto uniforme;
se invece la velocità è variabile, si ha moto
vario.
Moto rettilineo uniforme
Un corpo mobile si muove di moto uniforme quando la sua velocità è costante, cioè quando percorre spazi uguali in tempi uguali.
![]()
x= spazio [ m ]
t= tempo [ s ]
v= velocità [ m/s ]
Il moto vario è caratterizzato da una velocità variabile.
In questo caso, non avendo la velocità istantanea si considera la velocità
media vm come rapporto fra lo spazio e il tempo.
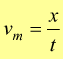
Più precisamente supponendo che l'asse OX coincida con la traiettoria.
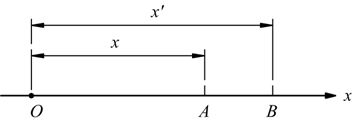
Se l'oggetto si trova nella posizione A ( distanza x rispetto all'origine
O) al tempo t mentre la sua posizione è B (distanza x' rispetto ad O) al
tempo t'; la velocità media fra A e B è definita da:
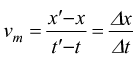
La velocità media durante un certo intervallo di tempo è uguale allo spostamento
medio per unità di tempo durante l'intervallo di tempo stesso Per determinare
la velocità istantanea nel punto A, dobbiamo prendere l'intervallo di tempo
Δt più piccolo possibile, in modo che non avvengano essenzialmente
variazioni nello stato di moto durante l'intervallo di tempo stesso; dal
punto di vista matematico.
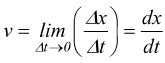
otteniamo, in tal caso la velocità istantanea.
Se conosciamo il legame tra velocità e tempo: $v=f(t)$ possiamo
risolvere l'eq.precedente rispetto a x mediante integrazione infatti scrivendo
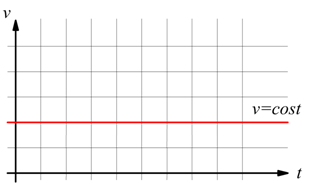
$dx=v⋅dt$; nel caso del moto rettilineo uniforme , v=cost.
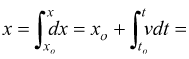
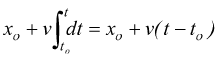
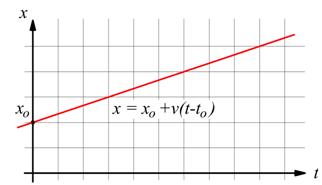
cioè: $x=x_o+v(t - t_o)$ ovviamente
se assumiamo che la posizione iniziale
$x_o=0$ e che il tempo iniziale sia $t_o=0$, riotteniamo
l'espressione iniziale: $x=v⋅t$.
Moto uniformemente accelerato
Il moto vario si dice accelerato quando
la velocità aumenta, è invece ritardato
quando la velocità diminuisce .
L'accelerazione è l'aumento della velocità
nell'unità di tempo. La decelerazione
è la diminuzione della velocità nell'unità di tempo, può essere considerata
un'accelerazione negativa. Senza considerare l'analisi matematica l'accelerazione
viene definita come :
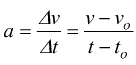 con
con
vo=velocità iniziale
to=tempo iniziale
se vo=0 e to=0 risulta:
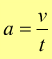 [
m/s2 ] quindi:
[
m/s2 ] quindi: ![]()
con le stesse ipotesi, la velocità media è $$v_m={v+v_o}/2$$ ; che se $v_o=0$ diventa: $$v_m=v/2$$ cioè
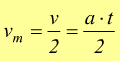
sapendo che lo spazio percorso è pari alla velocità media per il tempo:
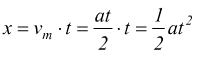 ( partendo
da fermi )
( partendo
da fermi )
Per l'analisi matematica, la velocità di un corpo è funzione del tempo.
Se la velocità rimane costante il moto si dice uniforme. Supponendo che
all'istante t l'oggetto si trova in A con velocità v e che all'istante t'
sia in B con velocità v l'accelerazione media fra A e B è definita :
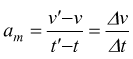
Così l'accelerazione media durante un certo intervallo di tempo è la variazione
della velocità per unità di tempo durante l'intervallo di tempo stesso.
L'accelerazione istantanea è il valore limite dell'accelerazione media quando
l'intervallo Δt diventa piccolo a piacere.
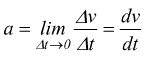
cosicché abbiamo ottenuto l'accelerazione istantanea calcolando la derivata
della velocità rispetto al tempo.
In generale l'accelerazione varia durante il moto.
Se in un moto rettilineo l'accelerazione è costante il moto si dice
uniformemente accelerato.
Se conosciamo l'accelerazione possiamo calcolare la velocità integrando
l'equazione precedente:
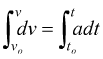 essendo
vo la velocità all'istante to;
essendo
vo la velocità all'istante to;
dato che 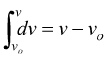 abbiamo:
abbiamo: 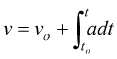
dall'equazione precedente (integrando) supponendo il tempo iniziale to=0
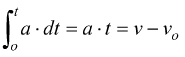 avremo poi:
avremo poi:
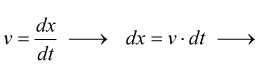
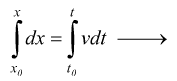
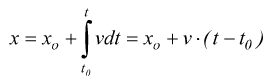
![]() spazio nel
moto rettilineo uniforme
spazio nel
moto rettilineo uniforme
qualora la velocità non fosse uniforme ma ci fosse una accelerazione 'a':

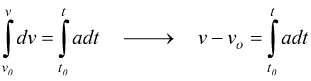
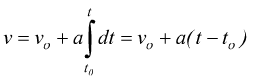 nell'ipotesi
di considerare to=0
nell'ipotesi
di considerare to=0
![]() velocità
nel moto
uniformemente accelerato
velocità
nel moto
uniformemente accelerato
sapendo che 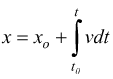
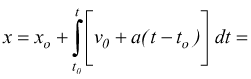
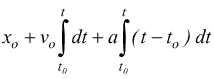 avremo:
avremo:
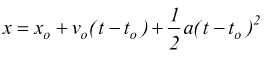
ponendo $x_o=0$ e $t_o=0$.
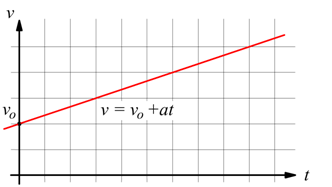
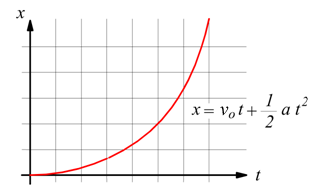
Se il moto uniformemente accelerato si verifica quando è in corpo è dotato
già di moto uniforme, con velocità vo .
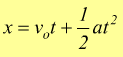 spazio
nel moto rettilineo uniformemente accelerato
spazio
nel moto rettilineo uniformemente accelerato
Il segno è positivo se il moto è accelerato negativo nel caso di moto ritardato.
Nel caso di un corpo che cade per gravità al suolo (caduta di un grave)
si ha un moto uniformemente accelerato con accelerazione g= 9,81 m/s2.
![]()
![]()
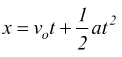 se
la velocità iniziale vo=0
se
la velocità iniziale vo=0 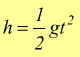
Con h altezza della caduta; essendo ![]() avremo:
avremo:
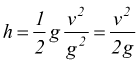 In
definitiva sarà:
In
definitiva sarà: ![]()
Combinando due delle formule precedentemente trovate per il moto uniformemente accelerato è possibile ottenere una importante relazione che lega tra loro velocità, spazio e accelerazione, indipendentemente dal tempo.
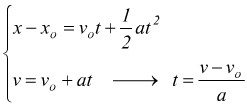
sostituendo questa espressione del tempo nella prima equazione del sistema si avrà
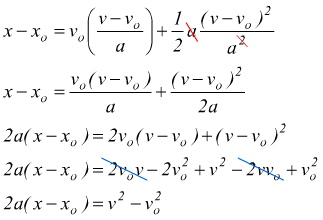
si ottiene dunque ![]()
Ricordiamoci poi, che se tra le due formule del moto rettilineo
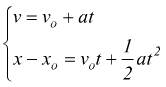
eliminiamo l'accelerazione
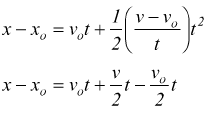
otteniamo un'ulteriore utile relazione
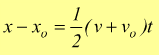
 edutecnica
edutecnica