Polinomi
Un polinomio è la somma algebrica i più monomi.
I monomi che costituiscono gli addendi del polinomio vengono chiamati termini
del polinomio.
Sono polinomi 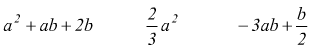
Un polinomio viene anche chiamato binomio, trinomio o quadrinomio a secondo che sia formato da due, tre o quattro monomi
7x2+y3 ⟵
è un binomio
3a+4y2-2 ⟵ è un trinomio
a+b-5c+d2 ⟵ è un quadrinomio
Un polinomio con tutti i suoi termini interi viene chiamato polinomio intero.
Un polinomio è chiamato frazionario (o fratto) solo se compaiono delle lettere
al denominatore.
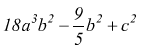 è
un polinomio intero
è
un polinomio intero
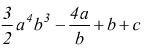 è
un polinomio fratto
è
un polinomio fratto
Se in un polinomio compaiono dei termini simili, conviene fare la riduzione
dei termini simili; cioè, sostituire a più termini simili un termine
simile ad essi, che abbia per coefficiente la somma algebrica dei coefficienti.
Il polinomio così ottenuto si dice ridotto a forma normale.
Ad esempio riduciamo in forma normale il polinomio ![]()

Se i termini del polinomio sono monomi tutti simili tra loro, il polinomio
si riduce ad un monomio.
Per questo motivo un monomio può essere considerato un caso particolare
di polinomio.
Il grado di un polinomio intero rispetto ad una lettera, è l'esponente maggiore
che ha quella lettera;invece, il grado complessivo dell'intero polinomio
è dato dal grado del termine che ha grado più elevato.

Un polinomio si dice ordinato secondo le potenze crescenti o decrescenti di una lettera, se i suoi termini sono disposti in modo che gli esponenti di quella lettera vadano crescendo o decrescendo.La lettera si chiama ordinatrice.
3ab+a2-5a4b2+2a5 è
ordinato secondo potenze crescenti di a.
2a4-3a2b+5ab-3 è
ordinato secondo potenze decrescenti di a
Un polinomio è chiamato omogeneo se tutti i suoi termini sono dello stesso grado Ad es.
2a3+ab2-3b3-2a2b è un polinomio omogeneo di terzo grado.
Si dice che un polinomio è completo rispetto ad una certa lettera, se contiene tutte le potenze di quella lettera, dalla massima fino alla potenza zero. In caso contrario, il polinomio, si dice incompleto.
Infatti, dalla potenza 5,decrescendo, sono presenti tutte le potenze di a: a5, a4, a3, a2, a1, a0.
Invece a5-2a3+a-2 è incompleto rispetto alla lettera a; mancano infatti le potenze a4 ed a2.
Addizione e sottrazione di polinomi
Un polinomio, così come un monomio, è una particolare espressione algebrica che rappresenta un numero; si capisce dunque, come si possa parlare di somma, differenza, prodotto e quoziente di polinomi, applicando gli stessi principi che si applicano nel caso delle operazioni tra i numeri.
Somma di polinomi:
Vediamo come possa essere eseguita la somma di due polinomi che abbiamo indicato tra parentesi, ovviamente separate dal segno +.
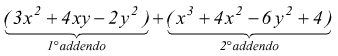
Successivamente, si eliminano le parentesi, ricordando che le parentesi precedute dal segno + si possono togliere lasciando inalterati i segni dei termini in esse contenuti. Potremo riscrivere la precedente espressione evidenziando i termini simili
![]()
eseguiamo poi la riduzione
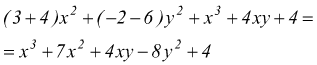
dall'esempio appena visto si conclude che l'addizione di due o più polinomi
si esegue scrivendo un unico polinomio che ha per termini tutti quelli dei
polinomi assegnati, ciascuno col proprio segno e operando poi, se possibile,
la riduzione dei termini simili.
Il polinomio ottenuto è la somma dei polinomi assegnati. Altro esempio
![]()
togliamo le parentesi lasciando invariati i segni dei termini racchiusi eseguendo la riduzione a termini simili
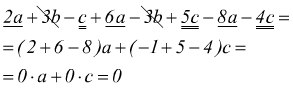
Tutti i termini si elidono tra loro ed il polinomio ottenuto è un polinomio nullo.
Differenza di polinomi:
E' possibile effettuare la differenza di polinomi scrivendoli, uno di seguito
all'altro, ciascun polinomio racchiuso tra parentesi,
separati dal segno -.
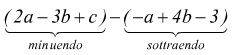
In seguito, si possono eliminare le parentesi, ricordandosi che la parentesi preceduta dal segno - si può togliere a patto di cambiare i segni di tutti i termini contenuti all'interno della parentesi stessa
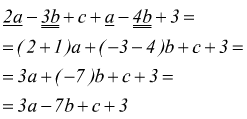
La sottrazione tra due polinomi, si esegue scrivendo un unico polinomio
ottenuto scrivendo i termini del primo polinomio (minuendo) col loro segno,
seguiti da quelli del secondo polinomio (sottraendo) cambiati
di segno ed eseguendo se possibile la riduzione ai termini simili.
Il polinomio che si ottiene è la differenza dei due polinomi, inizialmente
assegnati.
Osserviamo come se P è un certo polinomio definito (ad es.) come
P=3a-5b-7a2
possiamo indicare con -P il suo opposto
-P=-3a+5b+7a2
Dobbiamo constatare che la somma di un polinomio con il suo opposto dà
sempre zero (polinomio nullo).
Si riconosce, inoltre, che la differenza di due
polinomi è la somma del primo con l'opposto del secondo.
Come nel caso dei numeri relativi, l'insieme delle operazioni di somma e di differenza di polinomi viene chiamata somma algebrica di polinomi.
Prodotto di un polinomio per un monomio
Per moltiplicare un polinomio per un monomio, si moltiplica ciascun termine del polinomio per il monomio e si addizionano i prodotti parziali ottenuti ( si applica, cioè, la proprietà distributiva):
(a+b-c)m=am+bm-cm
ad es. calcolare il prodotto ![]()
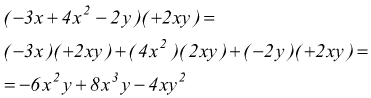
Prodotto di polinomi
Per moltiplicare un polinomio per un altro polinomio si moltiplica ciascun termine del primo di essi per ciascun termine dell'altro e si addizionano i prodotti parziali ottenuti, riducendo i termini simili. (si applica sempre la proprietà distributiva). Ad. es
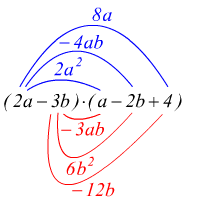
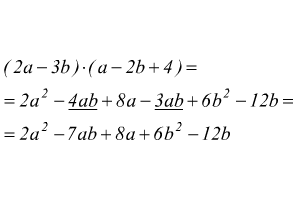
Altro esempio, calcolare il prodotto ![]()
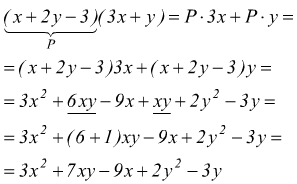
Divisione di un polinomio per un monomio
Per dividere un polinomio per un monomio si divide ciascun termine del polinomio per il monomio e si sommano i quozienti parziali ottenuti.
Si applica, cioè, la proprietà distributiva della divisione.
(a+b):c=a:b+b:c oppure
in forma equivalente
Un polinomio è divisibile per il monomio, se tutti i suoi termini sono divisibili per il monomio; in questo caso il quoziente è un polinomio intero. Il grado del quoziente è la differenza tra il grado del dividendo ed il grado del divisore. Ad es.
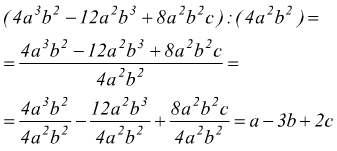
Se qualche termine del polinomio non è divisibile per il monomio, esso può rimanere indicato da una sua frazione.
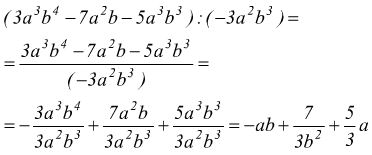
Bisogna poi ricordarsi che un polinomio è sempre divisibile per un numero diverso da zero ed il risultato della divisione è ancora un polinomio. Ad esempio per risolvere la seguente espressione, i due binomi devono essere divisi per dei numeri interi.
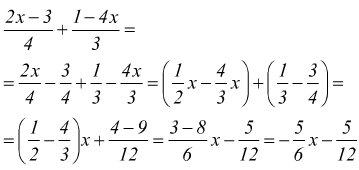
E' possibile effettuare le precedenti operazioni inserendo i polinomi nel
seguente modulo, rispettando la notazione Excel che prevede i simboli
(+) per la somma, (-) per la differenza, (*) per il prodotto, (/) per la
divisione, (^) per l'elevamento a potenza.
Raccoglimento a fattor comune
Se tutti i termini di un polinomio hanno un fattore comune, si può scrivere il polinomio sotto forma di un prodotto di due fattori, di cui uno è il fattore comune e l'altro è la somma algebrica dei quozienti di ciascun termine per il fattore comune.
Questa operazione si chiama "raccoglimento a fattor comune" oppure "mettere in evidenza un fattore". Generalmente il fattore messo in evidenza è il Massimo Comun Denominatore (M.C.D.) dei termini del polinomio. Esempi:
am+bm-cm=m(a+b-c)
m+abm-cm=m(1+ab-c)
M.C.D. ed m.c.m. di due polinomi
Se due o più polinomi sono divisibili per uno stesso polinomio , questo viene detto divisore comune dei polinomi assegnati.
Il Massimo comun divisore (M.C.D.) di due o più polinomi è quel polinomio che, fra tutti i divisori comuni dei polinomi assegnati, ha il grado maggiore.
Un polinomio che sia divisibile per due o più polinomi è detto multiplo comune dei polinomi assegnati.
Il minimo comune multiplo (m.c.m.) di due o più polinomi è quel polinomio che fra i multipli comuni dei polinomi assegnati è quello che ha grado minore.
Per calcolare M.C.D. ed m.c.m di due o più polinomi si scompongono i polinomi in prodotti di fattori e poi si applicano le regole già viste per i monomi, cioè:
Il M.C.D. è il prodotto dei fattori comuni, presi una sola valta col minore degli esponenti.
Il m.c.m. è il prodotto dei fattori comuni e non comuni presi una sola volta con il maggiore degli esponenti.
Ad es. calcolare il M.C.D. e il m.c.m. per i seguenti polinomi
(3a2+3ab) ; (3a3b+3a2b2)
; (6a3-6ab2)
; (9a3+18a2b+9ab2)
3a2+3ab=3a(a+b)
3a3b+3a2b2=3a2b(a+b)
6a3-6ab2=6a(a2-b2)=6a(a+b)(a-b)
9a3+18a2b+9ab2=9a(a2+2ab+b2)=9(a+b)2.
ottenendo
M.C.D.=3a(a+b)
m.c.m.=18a2b(a-b)(a+b)2
 edutecnica
edutecnica