Numeri

      

Il nostro sistema moderno di numerazione è decimale, perchè utilizza i dieci simboli:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Questi simboli sono chiamati cifre. Ad es.
0, 2, 4, 6, 8 sono le cifre pari
1, 3, 5, 7, 9 sono le cifre dispari.
I numeri si esprimono attraverso insiemi ordinati di cifre 6, 14, 436, 190... sono numeri .
I numeri che terminano (a destra) con una cifra pari, sono i numeri pari.
I numeri che terminano con una cifra dispari, sono i numeri dispari.

Il nostro sistema numerico è in base dieci, molto probabilmente, perchè gli esseri umani hanno ( sulle mani ) 10 dita; se gli esseri umani avessero avuto 8 dita, il nostro sistema numerico sarebbe stato molto probabilmente in base otto (sistema ottale) ma la cosa non avrebbe comunque avuto grandi conseguenze pratiche.

Come detto, il primo spunto per la costruzione di un sistema numerico è stato l'utilizzo delle dita delle mani; per questo motivo a quasi tutti i popoli è venuto spontaneo assumere come base dei loro sistemi di numerazione, il cinque o il dieci. Per quello che invece riguarda il modo di rappresentare i numeri, pare che il nostro sistema di numerazione abbia avuto origine in India attorno al 500 d.C per poi essere introdotto in Europa dagli arabi solo verso il 1200 d.C.

Numeri naturali

      

• L'insieme N dei numeri naturali contiene il numero 0.
• per ogni numero naturale n appartenente ad N, il numero il numero n+1 appartiene ancora ad n.

Assegnati due numeri naturali diversi tra loro,uno dei due è minore dell'altro.
Rispetto a questo ordinamento, lo 0 precede tutti i restanti numeri naturali, mentre non esiste alcun numero naturale che segue tutti gli altri.

Addizione in N

      

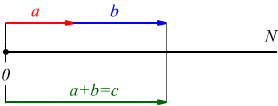
Sulla semiretta numerica, prima disegnata, possono essere facilmente interpretate le operazioni aritmetiche. Nel caso siano assegnati due numeri naturali qualsiasi a e b da sommare (a+b) bisogna solo contare per uno da sinistra verso destra a partire dal primo numero (a) tante volte quanto vale il secondo numero (b). Ad esempio se voglio fare la somma 2+3

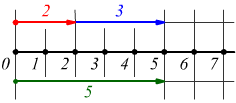
è sufficiente partire da 2 e fare 3 passi verso destra.

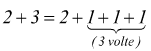
come si vede 2+3=5.

In generale assegnati due numeri a e b, per addizionarli è sufficiente partire da a e fare b passi di valore 1 verso destra .

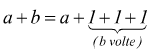
I numeri a e b si chiamano addendi, il numero che si ottiene si chiama somma.

                   

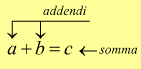
caso 1) se a=0 si fanno b passi a partire dall'origine della semiretta quindi 0+b=b
Ad es. 0+3=3

caso 2) se b=0 non ci si sposta dalla tacca che rappresenta a quindi a+0=a
Ad es. 5+0=5

La somma di due numeri naturali è sempre maggiore o uguale a ciascun addendo.

    Proprietà commutativa dell'addizione    

In una addizione, la somma non cambia se si cambia l'ordine degli addendi

       ad es.      3+5=5+3

    Proprietà associativa dell'addizione    
In una addizione di più addendi, la somma non cambia se a due (o più) addendi si sostituisce la loro somma.

        ad es.        (3+7)+6=10+6=16

ed è vero anche il contrario: ad un addendo si possono sostituire più numeri la cui somma è uguale a quella dell'addendo. Ad es.

10+6=(3+7)+6=3+7+6

questa peculiarità viene indicata, talvolta, come proprietà dissociativa della moltiplicazione.

    Elemento neutro rispetto all'addizione    

Dato che è 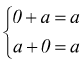              si può dire che l'addizione ha elemento neutro 0.

Moltiplicazione in N

      

La moltiplicazione tra due numeri naturali è una addizione ripetuta di tanti addendi uguali al secondo numero ripetute tante volte quanto sono indicate dal primo numero.

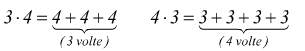
Come simboli per la moltiplicazione possono essere usati indifferentemente i simboli · oppure ×. comunque 3·4=12.
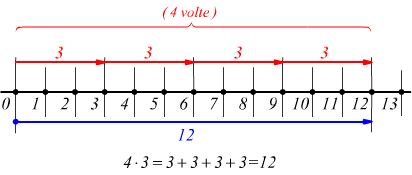
Nello stesso modo che si è visto per la somma, anche per la moltiplicazione è possibile dare una rappresentazione grafica dell'operazione.

    Proprietà commutativa della moltiplicazione    
In una moltiplicazione, il prodotto non cambia se si cambia l'ordine dei fattori

             ad esempio       2·5=5·2

    Proprietà associativa della moltiplicazione    
In una moltiplicazione di più fattori il prodotto non cambia se a due (o più) di essi si sostituisce il loro prodotto.

   ad es.

(3·4)·5=12·5=60
3·(4·5)=3·20=60
Anche in questo caso sarà ovviamente vero il viceversa
12·5=(3·4)·5=3·4·5

    Elemento neutro rispetto alla moltiplicazione    

Dato che è 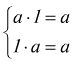        la moltiplicazione ha 1 come elemento neutro, perchè se 1 moltiplica qualunque numero, lo lascia invariato.

    Proprietà distributiva della moltiplicazione rispetto all'addizione    

Sia l'addizione che la moltiplicazione godono delle proprietà commutativa ed associativa.
Esiste una ulteriore proprietà che mette in relazione queste due operazioni e si tratta della proprietà distributiva.

Per moltiplicare un numero per una somma si può moltiplicare il numero per ciascun addendo della somma ed addizionare poi i prodotti ottenuti.

      ad es.

7·(3+4)=7·3+7·4 infatti
7·(3+4)=7·7=49
7·3+7·4=21+28=49

Bisogna dire che è valido anche il viceversa e l'operazione viene usualmente chiamata raccoglimento a fattor comune .

6·5+6·3 → 6·(5+3) → 66·8                      ed in generale si ha

Sottrazione in N

      

Ci si può chiedere se l'operazione di addizione sia reversibile (con un minimo di presupposti) cioè ci chiediamo se conoscendo il risultato ed uno degli operandi sia possibile trovare l'operando incognito, ad es. scrivendo
x+4=9 quindi x=?
quale è il valore di x? Molto semplice: il risultato è 5, perchè è l'unico numero che sommato a 4 ci fa ottenere il 9. In questo caso, abbiamo di fatto eseguito il calcolo inverso rispetto la somma e questo calcolo viene chiamato sottrazione. e si formalizza con la scrittura: 9-4=5 .

La sottrazione è l'operazione aritmetica che permette di calcolare la differenza tra due numeri di cui il primo è chiamato minuendo e il secondo sottraendo.

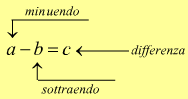
La differenza di due numeri, se esiste, è il numero che aggiunto al sottraendo fornisce come risultato il minuendo (differenza+sottraendo=minuendo). Cioè

15-9=6 perchè 6+9=15

    Proprietà invariantiva della sottrazione    

La differenza di due numeri non cambia, aggiungendo o togliendo lo stesso numero sia al minuendo che al sottraendo.
27-9=(27-7)-(9-7)=20-2=18           come
27-9=(27+1)-(9+1)=28-10=18

    Proprietà distributiva della moltiplicazione rispetto alla sottrazione    

Per moltiplicare una differenza indicata per un numero si può moltiplicare ogni termine della differenza per quel numero e poi sottrarre i prodotti ottenuti.

ovviamente la regola inversa a questa, coincide sempre con il raccoglimento a fattor comune.

NOTA :     La sottrazione non è sempre possibile da eseguire nell'insieme N, ad es. 7-12=? perchè il risultato non rientra in questo insieme; bisognerà introdurre una nuova classe di numeri : i numeri interi relativi (Z) per superare questo ostacolo formale.

Divisione in N

      

In modo analogo alla sottrazione, la divisione di due numeri naturali è l'operazione inversa della moltiplicazione. Prendiamo la moltiplicazione
5·x=15
chiedendoci quale è il numero (incognito) che moltiplicato per 5 restituisce 15. Molto facile, si tratta del 3. In questo modo, siamo autorizzati a scrivere

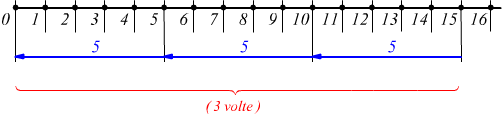
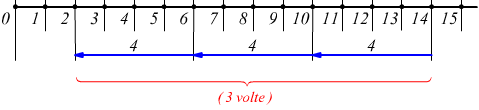
per arrivare allo zero (0) è sufficiente sottrarre al 15 il numero 5 per 3 volte, attraverso un meccanismo inverso a quello visto per la moltiplicazione. I termini della divisione prendono il nome di dividendo, divisore e quoziente.

Quando si fanno le divisioni, bisogna fare un minimo di attenzione, perchè ci sono delle regole da ricordare:

• Se il dividendo è uguale al divisore, il quoziente è uguale all'unità.

• Se il divisore è uguale ad 1, il quoziente è uguale al dividendo

• Se il dividendo è uguale a 0, il quoziente è uguale a 0 (con il divisore diverso da 0).

• Se il divisore è uguale a 0, senza che lo sia il dividendo, il quoziente non esiste: la divisione è impossibile.

nessun numero moltiplicato per 0 può dare 5. Quest'ultima regola è da ricordare: in una divisione, il divisore deve sempre essere diverso da 0.

In qualche modo, possiamo farci una ragione di questa regola: immaginiamo di dividere il 5 con dei numeri che si avvicinano progressivamente allo 0

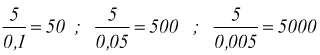
si nota, come più il divisore si avvicina allo zero, più il quoziente diventa grande, 'al limite' quando il divisore sarà 0 il quoziente sarà incommensurabilmente grande; cioè, sarà così grande che nemmeno il più potente dei calcolatori sarà in grado di calcolare.

cioè priva di significato, perchè qualsiasi numero moltiplicato per zero restituisce come prodotto zero.

Il resto

      

La divisione vista inizialmente 15:5=3 produce un quoziente esatto che viene chiamato quoto.

Il quoziente esatto, o quoto, tra due numeri interi a e b (con b≠0) è quel terzo numero c (se esiste) che moltiplicato per il divisore (b) restituisce il dividendo (a).

Quando il quoziente è esatto si può chiamare quoto.
Quando il quoziente non è esatto, esso viene chiamato solo quoziente.

Il quoziente tra due numeri interi (col divisore diverso da zero) è il più grande numero intero che moltiplicato per il divisore restituisce un prodotto non maggiore al dividendo.

non esiste un numero più grande del 3 che moltiplicato per 4 restituisca un prodotto non maggiore di 14.

Queste considerazioni, portano a concludere che come nel caso della sottrazione, anche la divisione non è sempre possibile all'interno dell'insieme dei numeri naturali.

Quando non si ha un quoziente esatto, il numero espresso dalla divisione non appartiene all'insieme N, ma all'insieme Q dei numeri razionali (o frazionari): un insieme più ampio che comunque, include N.

Per superare questa situazione formale, si introduce la nozione di resto.

Il resto di una divisione tra numeri interi è la differenza tra il dividendo ed il prodotto tra il divisore ed il quoziente.

resto=dividendo-(divisore×quoziente).

da cui si ha (divisore×quoziente)+resto=dividendo con resto < divisore

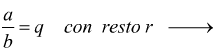
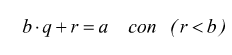
35:3=11 con resto 2 infatti 3×11+2=35

    Proprietà invariantiva della divisione    

Moltiplicando (o dividendo) i due termini della divisione per uno stesso numero diverso da zero, il quoziente non cambia, mentre il resto (se esiste) viene moltiplicato (o diviso) per lo stesso numero.

Come conseguenza di questa proprietà, avremo che: per dividere un prodotto per un numero, si può dividere uno dei fattori per quel numero e moltiplicare poi il quoziente esatto per gli altri fattori.

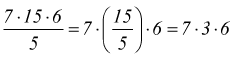
Quindi, per dividere un prodotto per uno dei suoi fattori basta sopprimere quel fattore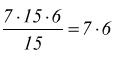      

    Proprietà distributiva della divisione    

Per dividere una somma (o una differenza) per un numero, divisore di ciascun termine della somma (o della differenza) si può dividere ciascun addendo per quel numero, per poi addizionare (o sottrarre) i quoti parziali.

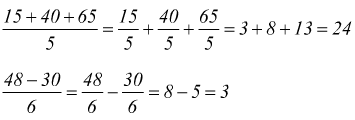
• Per dividere un numero per un quoziente , basta dividere quel numero per il dividendo e moltiplicare il risultato per il divisore

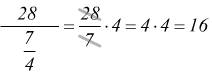
• Per moltiplicare un numero per un quoto indicato, si può moltiplicare quel numero per il dividendo e dividere il risultato per il divisore

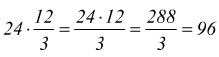        oppure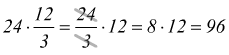        

• Per dividere, quando possibile, un numero per un prodotto indicato, si può dividere successivamente quel numero per ciascuno dei fattori del prodotto.

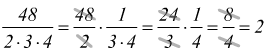
NOTA :     Ne la sottrazione ne la divisione godono della proprietà commutativa ed associativa.

13-6=7 mentre 6-13 non appartiene nemmeno ad N. Questo vale anche per la divisione: