Monomi
In aritmetica, per generalizzare i problemi, invece di numeri particolari
si usano le lettere minuscole dell'alfabeto (a, b, c, ..etc.) alle quali
si possono sostituire dei numeri qualsiasi, queste lettere sono chiamate
parametri.
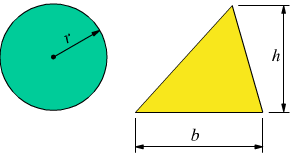
Sono ad esempio parametri la r nel calcolo dell'area di un cerchio
(π·r2) oppure la b (base) e la h (altezza) nel calcolo dell'area
di un triangolo (b·h/2) .
Un caso particolare è costituito dalle lettere x ed y che sono più comunemente indicate come indeterminate o incognite.
Un' espressione algebrica letterale, è un complesso di operazioni da eseguire su numeri e lettere. Ad esempio
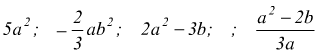
Un'espressione algebrica viene chiamata razionale intera, quando le operazioni indicate sono soltanto addizione, sottrazione, moltiplicazione ed elevamento a potenza
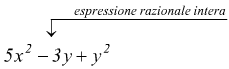
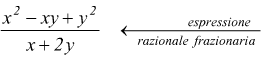
se invece tra le lettere appare anche l'operazione di divisione, l'espressione si dice razionale frazionaria.
La più semplice espressione letterale è il monomio.
Per quello che abbiamo accennato all'inizio, ad esempio, la formula per
calcolare l'area di un triangolo è un monomio
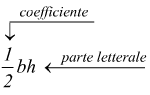
dove possono essere evidenziate una parte numerica chiamata coefficiente ed una parte letterale.
Un monomio è un' espressione letterale in cui appaiono solo operazioni di moltiplicazione tra le lettere, ed un eventuale coefficiente che può essere un numero reale qualsiasi.
sono monomi
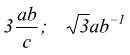non
sono monomi
come si vede l'operazione di elevamento a potenza è ammessa perchè la potenza
non è altro che una moltiplicazione ripetuta.
Non sono ammesse potenze ad esponente negativo nella parte letterale, perchè,
per le proprietà delle potenze, queste comportano una operazione di divisione
; infatti (ad es.)
queste limitazioni non riguardano il coefficiente che per la definizione di monomio può essere un numero reale qualsiasi; quindi
è
ammesso come coefficiente, perchè è un numero razionale e quindi reale
è
ammesso come coefficiente, perchè è un numero reale.
Se in un monomio appaiono più fattori numerici e più potenze della stessa
lettera, possiamo sostituire ai fattori numerici, il loro prodotto, e alle
varie potenze di ciascuna lettera, un'unica potenza di quella lettera.
In questo modo otteniamo un monomio ridotto a
forma normale. Ad es.
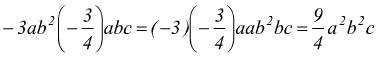
ogni monomio ridotto in forma normale ha un solo fattore numerico (parte numerica) che ricordiamo, si chiama coefficiente; mentre l'insieme dei fattori letterali, è la parte letterale del monomio.
Se in un monomio non appare il coefficiente si intende come sottinteso +1 o -1 a secondo che il monomio sia preceduto da + o da -.
● Il grado di un monomio intero, in forma normale, rispetto ad una certa lettera, è l'esponente di quella lettera.
● Il grado complessivo di un monomio, è uguale alla somma degli esponenti delle lettere che in vi appaiono.
è di grado 3 rispetto alla lettera a
è di grado 1 rispetto alla lettera b
è di grado 2 rispetto alla lettera c
il grado complessivo del monomio è 6.
● Due monomi sono uguali quando, ridotti in forma normale, hanno lo stesso coefficiente e la stessa parte letterale.
● Due monomi che hanno la stessa parte letterale ma coefficienti opposti,
si dicono monomi opposti.
Ad es. 3a3b2 e
-3a3b2 sono monomi opposti.
● Due o più monomi che hanno la stessa parte letterale si dicono monomi simili. Ad.es.
a3bc2 sono simili tra loro.
Somma algebrica di monomi
Per calcolare la somma di due o più monomi, questi devono essere scritti uno di seguito all'altro, ciascuno con il suo segno.
Per addizionare i monomi 2a2b;
-5ab3c2;
+7abc
si scrive 2a2b - 5ab3c2
+ 7abc
chiaramente, in generale, il risultato è un'espressione algebrica che non è un monomio.
Se ci sono due o più monomi simili, si fa la riduzione
dei termini simili, sostituendo ai monomi simili un monomio simile
ad essi che ha come coefficiente la somma algebrica dei coefficienti dei
monomi assegnati.
Supponiamo di dover addizionare i seguenti monomi
si scrive
infatti i tre monomi sottolineati sono simili perchè le loro parti letterali sono uguali ; si possono quindi ridurre ad un solo monomio, sommando i coefficienti
si deduce che la somma di due monomi opposti è 0.
Per facilitare il calcolo della somma algebrica di più monomi è sempre meglio sottolineare con segni particolari, i gruppi di monomi simili e di sopprimere (sbarrandoli) quelli opposti; si esegue, poi, la riduzione in termini simili. Ad es.
sottolineiamo i monomi simili ed eliminiamo i monomi opposti
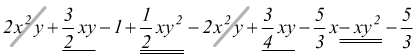
eseguiamo la riduzione ai termini simili
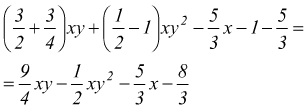
Prodotto di monomi
Il prodotto di due o più monomi è un monomio, che ha per coefficiente il prodotto dei coefficienti e, come parte letterale, le lettere comuni con esponente uguale alla somma degli esponenti, e le lettere non comuni con esponente immutato.
● esempio
qui si applicano le proprietà della moltiplicazione e delle potenze
in pratica si sommano gli esponenti delle singole lettere:
● esempio
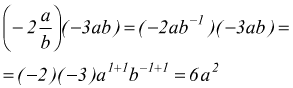
● esempio
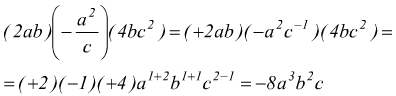
Potenza di un monomio
Per elevare a potenza con esponente intero un monomio, si eleva a quella potenza il coefficiente e si moltiplicano gli esponenti dei fattori letterali per l'esponente della potenza.
● esempio
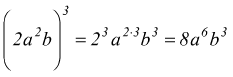
● esempio
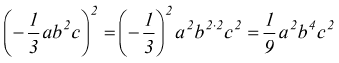
● esempio
Divisione di monomi
Il quoziente di due monomi è un monomio che ha come quoziente il quoziente dei coefficienti e per parte letterale tutte le lettere dei due monomi, prese ognuna una volta sola, con esponente uguale alla differenza degli esponenti che ciascuna lettera ha nel dividendo e nel divisore.
● esempio
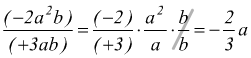
In pratica si sottraggono gli esponenti delle singole lettere
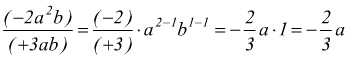
● esempio
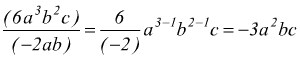
● esempio
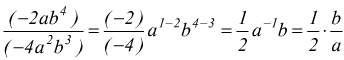
● esempio
Massimo Comune Divisore di monomi
Il Massimo Comun Divisore (M.C.D.) di due o più monomi è il monomio di grado massimo che divide ciascun monomio assegnato.
● esempio : supponiamo di dover calcolare l'MCD di tre monomi
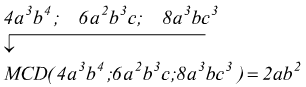
Infatti l'MCD tra 4, 6 e 8 è 2; delle lettere si
scelgono solo quelle comuni a tutti a tutti i termini, cioè, in
questo caso a e b .
La lettera c non c'è nel primo monomio e quindi non serve per l'MCD.
Gli esponenti della lettera a sono, nei tre monomi rispettivamente, 3;
2; 3, quelli della lettera b sono 4; 3; 1.
Per entrambe le lettere si sceglie l'esponente
minore: a2b è la parte letterale dell'MCD cercato.
Il M.C.D. di due o più monomi a coefficienti interi è il monomio che ha per coefficiente il M.C.D. dei coefficienti e, come parte letterale, le lettere comuni a tutti i monomi dati, ciascuna lettera presa una sola volta con l'esponente minore.
● esempio : trovare il M.C.D. tra
si ha
il segno potrebbe essere il + o anche il - ma normalmente si sceglie il segno +.
Se non tutti i coefficienti sono interi si assume, in genere, come coefficiente del MCD +1, che evidentemente si sottintende.
● esempio : trovare il M.C.D. dei i seguenti monomi
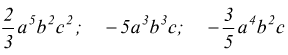
si ottiene
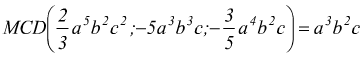
Minimo comune multiplo di monomi
Il minimo comune multiplo di due o pù monomi è
il monomio di grado minimo che sia divisibile per ciascuno dei monomi
dati.
Il m.c.m. di due o più monomi a coefficienti interi è il monomio che ha
per coefficiente il m.c.m. dei coefficienti e, come parte letterale le
lettere comuni e non comuni ai monomi assegnati, ciascuna di esse prese
una sola volta con il massimo esponente.
● esempio : calcolare il m.c.m. dei i seguenti monomi
si ha
Infatti il mcm tra 6; 4 e 2 è 12.
Le lettere si scrivono tutte con l'esponente più alto che ciascuna di
esse ha nei vari monomi di cui si deve cercare l'mcm.
Per la lettera a scegliamo l'esponente 4, il maggiore che appare tra i
vari monomi, per la lettera b scegliamo il l'esponente 3, per la c scegliamo
l'esponente 1, il maggiore possibile.
Il m.c.m. cercato è dunque 12a4b3c.
● esempio : calcolare il m.c.m. dei monomi
risulta:
il segno finale può essere + o - ma come nel caso del M.C.D. si sceglie abitualmente il +.
Se non tutti i monomi hanno coefficienti interi, si assume come coefficiente del m.c.m. +1 che naturalmente si sottintende.
● esempio : calcolare il m.c.m. dei seguenti monomi
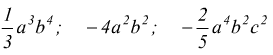
si ha:
Riassumiamo queste regole nel seguente schema dove, però, è possibile usare solo
coefficienti interi ed esponenti positivi.
Le operazioni consentite sono dunque la moltiplicazione (*) e l'elevamento a potenza (^).